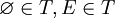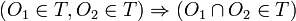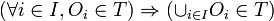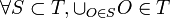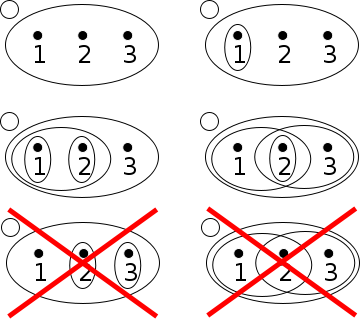Cuatro ejemplos y dos anti-ejemplos de topologías en el conjunto de tres puntos {1,2,3}. El ejemplo inferior izquierdo no es una topología porque la unión {2,3} de {2} y {3} no está definida; el ejemplo inferior derecho no es una topología porque la intersección {2} de {1,2} y {2,3} no está definida.

Un espacio topológico es una estructura matemática que permite la definición formal de conceptos como convergencia, conectividad, y continuidad. La rama de las matemáticas que estudia los espacios topológicos se llama topología.

Definición

Un espacio topológico es un conjunto E de elementos junto con T, una colección de subconjuntos de E que satisfacen las siguientes propiedades:

1. El conjunto vacío y E están en T.

1. La intersección de cualquier colección finita de conjuntos de T está también en T.

1. La unión de toda colección de conjuntos de T está también en T.

Esta condición también se puede escribir:

Los conjuntos en T son los conjuntos abiertos, y sus complementos en E son llamados conjuntos cerrados.

La colección T es llamada "topología" en E. Los elementos de E suelen llamarse puntos, aunque pueden ser cualquiera de los objetos matemáticos. Un espacio topológico en el cual los puntos son funciones es llamado un espacio funcional.

Al conjunto E se le llama substrato del espacio topológico.

Ejemplos

• Topología trivial o gruesa: es la formada por 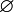y .
• Topología discreta: es la formada por el conjunto de las partes de E.
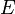• Topología de los complementos finitos: es la formada por y los conjuntos de , cuyos complementarios son finitos.
• R, conjunto de los reales, y T el conjunto de los intervalos abiertos en el sentido usual, y de las reuniones (cualesquiera) de intervalos abiertos.

Espacios metrizables

Toda métrica permite definir de manera natural en un espacio la topología formada por las uniones arbitrarias de bolas de centro r y radio d:

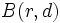
Esta topología se aproxima a la noción intuitiva de conjunto abierto, permitiendo una aproximación de carácter local a la topología.

En vez de considerar todo el conjunto, el punto de vista local consiste en preguntarse: ¿qué relación tiene que haber entre un punto a cualquiera de A, y A para que A sea un abierto?

Si se considera el ejemplo más conocido, el de los intervalos, uno se da cuenta de que los intervalos abiertos son los que no contienen puntos en su frontera o borde, que son puntos en contacto al la vez con A y con su complementario R - A.

En otras palabras, un punto de un abierto no está directamente en contacto con el "exterior".

No estar en contacto significa intuitivamente que hay una cierta distancia entre el punto y el exterior; llamémosla d. Entonces la bola B (a, d/2), de radio d/2 y de centro a está incluida en A y no toca el complementario. En la figura, a está en el interior de A, mientras que b está en su frontera, porque cualquier vecindad de b encuentra R - A.

Al hablar de distancia, utilizamos un concepto de los espacios métricos, que son más intuitivos pues corresponden al mundo real (asimilable a R³). En topología, tenemos que cambiar el concepto de bola por él, más general, de vecindad. Una vecindad de un punto x es este punto con algo de su entorno. Tenemos entera libertad para definir el significado de "entorno" y "vecindad" con tal de satisfacer los axiomas siguientes:

1. x pertenece a todas sus vecindades.
2. Un conjunto que contiene una vecindad de x es una vecindad de x.
3. La intersección de dos vecindades de x es también una vecindad de x.
4. En toda vecindad V de x existe otra vecindad U de x tal que V es una vecindad de todos los puntos de U.

Llamamos abierto un conjunto que es una vecindad para todos sus puntos.

Los axiomas expuestos en el punto de vista global están verificados:

1. E es obviamente una vecindad para todos sus puntos, y ∅ también porque no contiene punto. (Una propiedad universal: para todo x ... es forzosamente cierta en el conjunto vacío.)
2. Una unión de abiertos O_i es un superconjunto de cada O_i, y O_i es una vecindad de todos sus puntos, por lo tanto, la unión es una vecindad de todos sus puntos, gracias a la propiedad (2).
3. Sea x un punto de la intersección de los abiertos O₁ y O₂. O₁ y O₂ son abiertos que contienen x y por lo tanto vecindades de él. Una intersección de vecindades de x es una vecindad de x (propiedad 3), lo que implica que O₁ 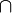O₂ es una vecindad de todos sus puntos, y por lo tanto un abierto.

Propiedades de un espacio topológico

• Compacidad
• Conectividad
• Axiomas de separación

Véase también

• Glosario de topología
• Topología

Bibliografía

• Munkres, James; Topology, Prentice Hall; 2nd edition (December 28, 1999). ISBN 0-13-181629-2.