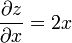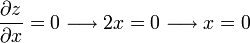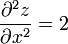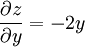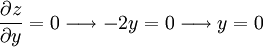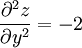Punto de silla

Punto de silla

Punto de silla

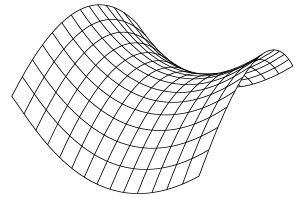
En una función de varias variables, si el gradiente en un punto se anula, puede haber un máximo, mínimo ó un punto de silla, que no es ni máximo ni mínimo. Es un punto en el que la función en una dirección crece, y en otra decrece. Debe su nombre a que las funciones en estos puntos tienen forma de silla de montar.

Ejemplo

Open Surface.svg

Un ejemplo típico es el Paraboloide hiperbólico, la función en R3:

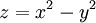z = {x}^2 - {y}^2 \,.

Para determinar sus extremos relativos, calculamos su derivada parcial respecto a x:

\frac{\partial z}{\partial x} = 2x \,

en el punto donde esta derivada valga cero, puede ser un extremo relativo:

\frac{\partial z}{\partial x} = 0 \longrightarrow 2x = 0 \longrightarrow x = 0 \,

en el punto x = 0 puede haber un extremo relativo, calculando su derivada segunda vemos:

\frac{\partial^2 z}{\partial x^2} = 2

que es un mínimo, esto es siguiendo el eje de las x, en el punto x = 0 la funcion presenta un mínimo relativo.

Veamos esto mismo en la dirección del eje de las y, su derivada parcial primera es:

\frac{\partial z}{\partial y} = -2y \,

Cuando esta derivada primera valga cero, puede presentar un extremo relativo:

\frac{\partial z}{\partial y} = 0 \longrightarrow -2y = 0 \longrightarrow y = 0 \,

en el punto y = 0, se da esta circunstancia, si vemos su derivada segunda tenemos:

\frac{\partial^2 z}{\partial y^2} = -2 \,

que toma valor negativo, luego este punto y = 0, es un máximo relativo, el punto x = 0, y = 0, es un punto de silla, dado que en la dirección de las x es mínimo y en la dirección de las y es un máximo.

Obtenido de "Punto de silla"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Punto de inflexión — Saltar a navegación, búsqueda Gráfico de y = x3 con un punto de inflexión en el punto (0,0). Gráfi …   Wikipedia Español

  • Silla (desambiguación) — La palabra silla puede referirse a: Asiento Silla, mueble para sentarse. Silla de rodilla, silla ergonómica diseñada para evitar malas posturas en la persona sentada Silla plegable, tipo de asiento liviano y portátil que puede ser almacenado… …   Wikipedia Español

  • Estación de Silla — Saltar a navegación, búsqueda Silla …   Wikipedia Español

  • Teoría del estado de transición — Figura 1: Diagrama de la coordenada de reacción para una reacción de sustitución nucleofílica (SN2) bimolecular entre bromometano y el anión hidróxido. La Teoría del Estado de Transición es una teoría que explica la velocidad de reacción de… …   Wikipedia Español

  • Matriz hessiana — En Matemática, la matriz hessiana de una función f de n variables, es la matriz cuadrada de n × n, de las segundas derivadas parciales. Contenido 1 Definición 2 Aplicación de la matriz hessiana 2.1 Concavidad/Convexidad …   Wikipedia Español

  • Estado de transición — Saltar a navegación, búsqueda El estado de transición en una reacción química es una configuración particular a lo largo de la coordenada de reacción que se define como el estado que corresponde al máximo de energía a lo largo de la misma. En… …   Wikipedia Español

  • Caos determinista — Saltar a navegación, búsqueda El caos y los fractales son parte de un tema mayor, la dinámica, rama de la física que empezó a mediados de 1600 cuando Isaac Newton descubrió las ecuaciones diferenciales, descubrió las leyes de movimiento y la… …   Wikipedia Español

  • Átomos en moléculas — Ejemplo de cuencas atómicas de un cristal de peruskita KCaF3 En amarillo los átomos de Calcio, en verde los Fluor y en rojo los Potasio. El planteamiento de la teoría de átomos en móleculas es un modelo químico cuántico que caracteriza el enlace… …   Wikipedia Español

  • Pseudoesfera — Saltar a navegación, búsqueda Pseudoesfera Tractriz (curva en azul) …   Wikipedia Español

  • Camino óptico — Camino óptico(L) (o longitud de camino óptico) es la distancia recorrida, a la velocidad de la luz en el vacío, en el tiempo t empleado por la luz para recorrer la distancia l en un medio con índice de refracción n. Teniendo en cuenta que podemos …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”