La razón aritmética de dos cantidades es la diferencia (o resta) de dichas cantidades. La razón aritmética se puede escribir colocando entre las dos cantidades el signo . o bien con el signo -. Así, la razón aritmética de 6 a 4 se escribe: 6.4 ó 6-4.

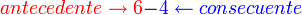
El primer término de una razón aritmética recibe el nombre de antecedente y el segundo el de consecuente. Así en la razón 6-4, el antecedente es 6 y el consecuente 4.

Propiedades de las razones Aritméticas

Como la razón aritmética de dos cantidades no es más que la resta indicada de dichas cantidades, las propiedades de las razones aritméticas serán las propiedades de toda suma o resta.

PRIMERA PROPIEDAD

Si al antecedente se le suma o resta una cantidad la razón aritmetica queda aumentada o disminuida dicha cantidad.

• Primer caso (con la suma)

Sea la razón aritmetica 7 a 5 es igual a 2:

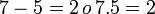
Si le sumamos al antecedente el número 4 (aclaramos que puede ser cualquier número) entonces tendríamos (7+4)-5= 6. Como se observa la respuesta de la razón aritmética original (7-5=2), después de sumarle 4 al antecedente ((7+4)-5= 6) la respuesta queda aumentada en dicha cantidad.

• Segundo caso (con la resta)

Sea la razón aritmetica 18 a 3 es igual a 15:

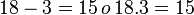
Si le restamos al antecedente el número 2 (aclaramos que puede ser cualquier número) entonces tendríamos (18-2)-3= 13. Como se observa la respuesta de la razón aritmética original (18-3=15), después de restarle 2 al antecedente ((18-2)-5= 13) la respuesta queda disminuida en dicha cantidad.

SEGUNDA PROPIEDAD

Si al consecuente de una razón aritmética se suma o se resta una cantidad cualquiera, la razón queda disminuida en el primer caso y aumentada en el segundo en la cantidad de veces que indica dicho número.

• Primer caso (sumando una cantidad cualquiera al consecuente)

td eso es una mamaera

Sea la razón aritmetica 45 a 13 es igual a 32:

Si le sumamos al consecuente el número 7 (aclaramos que puede ser cualquier número) entonces tendríamos 45-(13+7)=25. Como se observa la respuesta de la razón aritmética original (45-13=32), después de sumarle 7 al consecuente 45-(13+7)=25) la respuesta queda disminuida en dicha cantidad es decir de 32 paso a ser 25.

• Segundo caso (restando una cantidad cualquiera al consecuente)

Sea la razón aritmetica 36 a 12 es igual a 24:

Si le restamos al consecuente el número 3 (aclaramos que puede ser cualquier número) entonces tendríamos 36-(12-3)= 27. Como se observa la respuesta de la razón aritmética original (36-12=24), después de restarle 3 al consecuente (36-(12-3)= 27) la respuesta queda aumentada en dicha cantidad es decir de 24 paso a ser 27.

Proporciones Aritméticas

Una "proporción aritmética" es la = de 2 razones. Las proporciones aritméticas se pueden representar de dos maneras distintas:

• a/b = c/d o bien
• a:b = c:d

y se lee "a es a b como c es a d".

Los términos primero y cuarto de una proporción aritmética reciben el nombre de extremos, mientras que los términos segundo y tercero se denominan medios. Los términos primero y tercero reciben el nombre de antecedentes, mientras que los términos segundo y cuarto se llaman consecuentes.

Así sea la proporción aritmética 10:5 = 8:4. Los términos 10 y 4 (son extremos) y, 5 y 8 (son medios).

Las proporciones aritméticas cuyos medios no son iguales reciben el nombre de proporciones aritméticas discretas. Por el contrario, si los medios de la proporción aritmética son iguales, ésta recibe el nombre de continua. En el caso del ejemplo se trata de una proporción aritmética discreta porque sus medios son desiguales (5 y 8).

En toda proporción (no continua):

• El producto de los extremos será igual al producto de los medios.

(10×4 = 5×8)

Se define la media aritmética de una proporción aritmética continua como cada uno de los medios iguales de dicha proporción aritmética. Sea: 10-8::8-6. La media aritmética es 8.

La media aritmética de una proporción aritmética es igual a la semisuma de los extremos.

La razón geométrica de dos números es el cociente exacto de dividir el primero a por el segundo b y se representa:

a:b

Se lee "a" es a "b" como "c" es a "d"

Donde el a, b son entero, fraccionario o mixto (desde el punto de la aritmética).

Las razones se pueden escribir de tres maneras diferentes:

Ejemplo:

2 es a 20

2:1 /1

2/1

Por lo tanto toda razón se puede expresar como una fracción y eventualmente como un decimal.