Aritmética

Alegoría de la Aritmética.
Pintura de Laurent de La Hyre.

La aritmética (del lat. arithmetĭcus, y este del gr. ἀριθμητικός,^[1] ἀριθμός = número) es la rama de la matemática cuyo objeto de estudio son los números y las operaciones elementales hechas con ellos: suma, resta, multiplicación y división.

Al igual que en otras áreas de la matemática, como el álgebra o la geometría, el sentido de «la aritmética» ha ido evolucionando con el progresivo desarrollo de las ciencias. Originalmente, la aritmética se desarrolla de manera formal en la Antigua Grecia, con el refinamiento del rigor matemático y las demostraciones, y su extensión a las distintas disciplinas de las «ciencias naturales».^[2] En la actualidad, puede referirse a la aritmética elemental, enfocada a la enseñanza matemática básica; también al conjunto que reúne el cálculo aritmético y las operaciones matemáticas, específicamente, las cuatro operaciones básicas aplicadas ya sea a números (naturales, fracciones, etc.) como a entidades matemáticas más abstractas (matrices, operadores, etc); también a la así llamada alta aritmética,^[3] mejor conocida como teoría de números.

Las operaciones aritméticas

Suanpan:ábaco chino.

• Las cuatro operaciones básicas (o elementales) de la aritmética son:
  • Suma
  • Resta
  • Multiplicación
  • División

Instrumentos de cálculo

• Cálculo mental
• Contar con los dedos
• Varillas de conteo
• Ábacos o calculadoras mecánicas
• Máquina de sumar
• Calculadora de bolsillo

Historia

Edad antigua

Hay evidencias de que los babilonios tenían sólidos conocimientos de casi todos los aspectos de la aritmética elemental hacia 1800 a. C., gracias a transcripciones de caracteres cuneiformes sobre tablillas de barro cocido, referidas a problemas de geometría y astronomía. Solo se puede especular sobre los métodos utilizados para generar los resultados aritméticos - tal y como se muestra, por ejemplo, en la tablilla de arcilla Plimpton 322, que parece ser una lista de ternas pitagóricas, pero sin mostrar cómo se haya generado la lista.

Los Shulba Sutras recopila los conocimientos matemáticos de la India durante el período védico; constan de datos geométricos e incluyen el problema de la cuadratura del círculo. Datados de una época que oscila entre los 800 a. C. y los 200 a. C.

Otras civilizaciones mesopotámicas como sirios y fenicios alcanzaron grados de desarrollo matemático similares, que utilizaron tanto para el comercio como para la resolución de ecuaciones algebraicas.

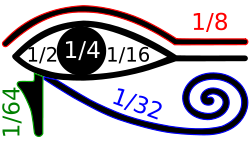
El sistema de numeración egipcio, basado en fracciones unitarias, permitía efectuar cuentas aritméticas avanzadas, como se muestra en papiros conservados como el el Papiro de Moscú o el Papiro de Ahmes (que data de ca. 1650 a. C., aunque es una copia de un antiguo texto de ca. 1850 a. C.) que muestra sumas, restas, multiplicaciones y divisiones, utilizando un sistema de fracciones, así como los problemas de determinar el volumen de una esfera, o el volumen de una pírámide truncada. El papiro de Ahmes es el primer texto egipcio que menciona los 365 días del calendario egipcio, el primer calendario solar conocido.

Antigüedad clásica

Nicómaco de Gerasa (ca. 60 - 120 a. C.) resume la filosofía de Pitágoras enfocada a los números, y sus relaciones, en su Introducción a la Aritmética. Arquitas (428 a.C. - 347 a.C.) sostiene que la matemática está constituida por la astronomía, la geometría, la aritmética y la música. El quadrivium (lat. "cuatro caminos"), agrupaba las disciplinas científicas relacionadas con las matemáticas; proviene de la escuela pitagórica. De las siete artes liberales en que se organizaban los estudios formales en la Antigüedad y la Edad Media, la aritmética era parte de las enseñanzas escolásticas y universitarias.

Edad Media

Las operaciones aritméticas, aún las más básicas, resultaban muy complicadas con numerales romanos; en 1202, Fibonacci, en su tratado Liber Abaci, introduce el sistema aprendido de los árabes, el moderno sistema de numeración decimal con números arábigos. La importancia práctica en contabilidad hizo que las nuevas técnicas aritméticas se popularizaran enseguida en Europa. Fibonacci llegó a escribir que «comparado con este nuevo método, todos los demás habían sido erróneos». En el siglo VII, el obispo sirio Severo Sebhokt menciona este método con admiración, indicando no obstante que el método indio iba más allá de esa descripción. Los árabes aprendieron ese nuevo método y lo llamaron hesab.

La aritmética india era mucho más simple que la aritmética griega, debido a la simplicidad del sistema numérico indio que, además, poseía el cero y una notación con valor numérico posicional.

Civilizaciones precolombinas

Quipu.

Al igual que otras civilizaciones mesoamericanas, los mayas utilizaban un sistema de numeración de base vigesimal (base aritmética 20), para medir el tiempo y participar del comercio a larga distancia. Los mayas preclásicos desarrollaron independientemente el concepto de cero alrededor del año 36 a. C.^[4] Aunque poseían sistema de numeración, la ciencia maya y azteca estaba más enfocada en predecir el paso del tiempo, elaborar calendarios y pronosticar eventos astronómicos. Las culturas andinas, que no poseían sistema de escritura, sí parecen haber desarrollado más el cálculo aritmético. Algunas inscripciones fijan con gran precisión el año solar real en 365 días. Fueron las primeras civilizaciones en inventar el cero, aunque con algunas peculiaridades que le privaron de posibilidad operatoria.^[5]

Los incas se destacaron principalmente por su capacidad de cálculo para fines económicos y comeriales. Los quipus y yupanas fueron señal de la importancia que tuvo la administración incaica. Esto dotó a los incas de una aritmética sencilla pero efectiva, para fines contables; basada en el sistema decimal; conocieron el cero, y dominaron la suma, la resta, la multiplicación y la división.

Aritmética en Asia

Varillas de conteo.

La matemática china temprana es tan diferente a la de otras partes del mundo, que es razonable suponer que se desarrolló independientemente. El texto de matemáticas más antiguo que se conserva es el Chou Pei Suan Ching (literalmente: La Aritmética Clásica del Gnomon y los Senderos Circulares del Cielo), datado de 300 a.C.^[6]

De particular notoriedad es el uso de un sistema decimal posicional, la así llamada numeración con varillas, utilizada muchos siglos antes del sistema indoarábigo de numeración.^[6] El sistema de numeración con varillas permitía representar cantidades arbitrariamente grandes, y facilitaba el cálculo matemático con suanpan (o ábaco chino). La fecha de invención del "suan pan" es incierta, pero los registros escrito más antiguos que lo mencionan datan del año 190 a.C., en las «Notas Suplementarias en el arte de las Figuras», de Xu Yue.

Las nueve lecciones del arte matemático, contiene problemas de agricultura, comercio, geometría, ingeniería así como trabajos con triángulos rectángulos y aproximaciones al número π. Zu Chongzhi calcula el valor de π hasta siete decimales.^[6]

La matemática hindú alcanzó su madurez durante los siglos I al VIII, con el invento trascendental de la notación posicional empleando la cifra cero como valor nulo. Utilizaron, como en occidente, un sistema de numeración de base 10 (con diez dígitos). Egipcios, griegos y romanos, aunque utilizaban un sistema decimal, este no era posicional, ni poseía el cero, el cual fue transmitido a occidente mucho más tarde, por los árabes, a través de la España e Italia medievales. Las múltiples ventajas prácticas y teóricas del sistema de «notación posicional con cero» dieron el impulso definitivo a todo el desarrollo ulterior de las matemáticas.

El sistema de numeración decimal aparece ya en el Süryasiddhanta, pequeño tratado que data probablemente del siglo VI. Los trabajos matemáticos de los hindúes se incorporaron en general a las obras astronómicas. Este es el caso de Aryabhata, nacido hacia 476, y de Brahmagupta, nacido hacia 598. Hacia 1150, Bhaskara escribió un tratado de aritmética en el que exponía el procedimiento del cálculo de raíces cuadradas. Se trata de una teoría de las ecuaciones de primer y segundo grado, no en forma geométrica, como lo hacían los griegos, sino en una forma que se puede llamar algebraica.

Los modernos algoritmos de cálculo fueron posibles gracias a la introducción de los números árabes y la notación decimal posicional.

Aritmética árabe

La matemática hindú, con el temprano desarrollo de la notación posicional y uso del cero, revistieron gran importancia en el progreso matemático posterior. Esta herencia fue recogida por los árabes, netamente con los trabajos de al-Jwarizmi y las primeras traducciones de textos griegos al árabe, incluyendo los Elementos de Euclides realizada por al-Hajjaj. En la Casa de la sabiduría (Bayt al-Hikma, una institución de investigación y traducción establecida en Bagdad), los científicos y matemáticos tradujeron las obras de Euclides, Diofanto, Menelao, Arquímedes, Ptolomeo, Apolonio entre otros clásicos de la ciencia griega. Uno de los avances más significativos se da con los trabajos de Abu Yafar Mohamed ibn Musa al-Jwarizmi: el álgebra,^[7] que representaba un apartamiento revolucionario del concepto geometricista de los griegos, permitiendo un tratamiento distinto de los "objetos" tales como los números racionales, los irracionales o las magnitudes geométricas, y una aplicación sistemática de la aritmética al álgebra.^[8] Abu Bekr ibn Muhammad ibn al-Husayn al-Karaji, nacido en 953, es probablemente el primero en liberar completamente al álgebra de las operaciones geométricas y remplazarlas por el tipo de operaciones aritméticas que constituyen el corazón del álgebra actual. al-Samawal (nacido en 1130) fue el primero en dar al nuevo tópico del álgebra una descripción precisa, cuando escribió que ella se ocupaba ...de operar sobre las incógnitas usando todas las herramientas aritméticas, de la misma forma que el aritmético opera sobre lo conocido. Thabit ibn Qurra (nacido en 836), hizo múltiples contribuciones en los más diversos campos de las matemáticas, en especial a la teoría de números.

Tres distintos tipos de sistemas aritméticos se empleaban simultáneamente alrededor del siglo X: la aritmética por conteo con los dedos, con los numerales enteramente escritos en palabras, era el método empleado por la comunidad mercantil; el sexagesimal, con los numerales denotados por letras del alfabeto árabe, provenía de la matemática babilónica, y los matemáticos del islam lo usaron principalmente para el trabajo astronómico; el tercer sistema fue la aritmética de los numerales indios y las fracciones con valor posicional decimal.

Alta aritmética

El término aritmética también hace referencia a la teoría de números. Esto incluye las propiedades de los números enteros relacionadas con su primalidad, divisibilidad y las soluciones de ecuaciones en los enteros, así como las investigaciones modernas que profundizan estos temas. Es en este contexto que se encuentra «teorema fundamental de la aritmética» y las «funciones aritméticas»; este es el uso reflejado en A Course in Arithmetic de Jean-Pierre Serre, o el que le da Harold Davenport en frases como: "aritmética de primer orden" o "alta aritmética".

• La aritmética modular trata de las congruencias de números enteros; su estudio se insribe dentro de la teoría de números.
• La aritmética binaria y el álgebra de Boole, muy utilizadas en informática, es el cálculo aritmético efectuado en un sitema de numeración binario, y el álgebra resultante. Documentado por Leibniz, en el siglo XVII, en su artículo Explication de l'Arithmétique Binaire.
• La aritmética ordinal, en teoría de conjuntos, describe el cálculo aritmético con las operaciones —suma, multiplicación y exponenciación— aplicadas a los números ordinales.
• La aritmética de Peano es el conjunto de axiomas de construcción de los números naturales.
• Teoremas de incompletitud de Gödel, enunciados por Gödel en 1930, demuestra que ninguna teoría matemática formal capaz de describir los números naturales y la aritmética con suficiente expresividad, es a la vez consistente y completa.

El Teorema Fundamental de la Aritmética

También conocido como teorema de factorización única, afirma que todo entero positivo se puede representar de forma única como producto de factores primos. Este resultado fue obtenido por Euclides, y presentado originalmente como un corolario al llamado Primer Teorema de Euclides.^[9] La demostración formal no se dio hasta la publicación de las Disquisitiones Arithmeticae por Carl Friedrich Gauss en 1801. La generalización y profundización de este resultado y otros similares, son los que impulsan el desarrollo de la teoría de números.

Escritos relacionados con la aritmética

Véase también

Notas y referencias

Bibliografía

• Referencia global en Encyclopaedia of Mathematics
• MathWorld article about arithmetic
• Referencia global en History Index
• «Mathematics in various cultures». Consultado el 3 de septiembre de 2011.
• Cut the knot article What is arithmetic?
• Wussing, Hans (1998). Lecciones de historia de las matemáticas. Siglo XXI de España Editores. 
• Collette, Jean-Paul (1985). Historia de las matemáticas (volúmenes 1 y 2). Madrid: Siglo XXI Editores S.A.. ISBN 84-323-0526-4. 

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre Aritmética. Commons
• Portal:Matemática. Contenido relacionado con Matemática.
• Wikcionario tiene definiciones para aritmética.Wikcionario