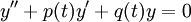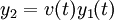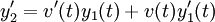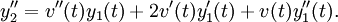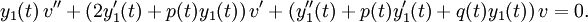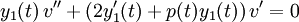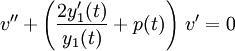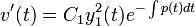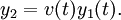Reducción de orden

Saltar a navegación, búsqueda

En matemáticas, la reducción de orden es una técnica utilizada para resolver ecuaciones diferenciales ordinarias de segundo orden. Se utiliza cuando la primera de dos soluciones ( $y 1$ ) es conocida y se busca la segunda ( $y 2$ ).

Uso

Dada una ecuación diferencial

$y''+p(t)y'+q(t)y=0\,$

y una sola solución ( $y 1 (t)$ ), y sea la segunda solución definida por

$y_2=v(t)y_1(t)\,$

donde $v (t)$ es una función arbitraria. Así,

$y_2'=v'(t)y_1(t)+v(t)y_1'(t)\,$

$y_2''=v''(t)y_1(t)+2v'(t)y_1'(t)+v(t)y_1''(t).\,$

Si se sustituyen por $y$ , $y'$ , y $y''$ a la ecuación diferencial, entonces

$y_1(t)\,v''+(2y_1'(t)+p(t)y_1(t))\,v'+(y_1''(t)+p(t)y_1'(t)+q(t)y_1(t))\,v=0.$

Como $y 1 (t)$ es solución de la ecuación diferencial original, $y 1''(t) + p (t) y 1'(t) + q (t) y 1 (t) = 0$ , se puede reducir a

$y_1(t)\,v''+(2y_1'(t)+p(t)y_1(t))\,v'=0$

que es una ecuación diferencial de primer orden por $v'(t)$ . Dividiendo por $y 1 (t)$ , se obtiene

$v''+\left(\frac{2y_1'(t)}{y_1(t)}+p(t)\right)\,v'=0$

y $v'(t)$ se puede encontrar utilizado el método general:

$v'(t) = C_1y_1^2(t)e^{-\int p(t)dt}$

Una vez se ha encontrado $v'(t)$ , se integra y se sustituye a la ecuación original por $y 2$ :

$y_2=v(t)y_1(t).\,$

Referencias

(en inglés) W. E. Boyce and R. C. DiPrima, Elementary Differential Equations and Boundary Value Problems (8th edition), John Wiley & Sons, Inc., 2005. ISBN 0-471-43338-1.
(en inglés) Eric W. Weisstein, Second-Order Ordinary Differential Equation Second Solution, From MathWorld--A Wolfram Web Resource.

Obtenido de "Reducci%C3%B3n de orden"

Categoría: Ecuaciones diferenciales ordinarias

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

Orden (desambiguación) — Orden puede adqurir varios significados en diferentes disciplinas. Puede referirse a: Contenido 1 Teoría de sistemas 2 Criterios de ordenación 3 Significados en diferentes ciencias 3.1 … Wikipedia Español
Nuevo Orden Mundial (conspiración) — El lema Novus Ordo Seclorum ( Nuevo Orden de los Siglos ) aparece también en el reverso del Gran Sello de los Estados Unidos, e, igualmente, se encuentra inscrito en el reverso de los billetes de dólar estadounidenses. El Nuevo Orden Mundial… … Wikipedia Español
Cálculo lambda — Artículo parcialmente traducido: Contiene texto en inglés. Ayuda a terminarlo. El cálculo lambda es un sistema formal diseñado para investigar la definición de función, la noción de aplicación de funciones y la recursión. Fue introducido por… … Wikipedia Español
Mecánica hamiltoniana — La mecánica hamiltoniana fue formulada en 1833 por William R. Hamilton. Como la mecánica lagrangiana, es una reformulación de la mecánica clásica. La mecánica hamiltoniana puede ser formulada por sí misma, usando los espacios simplécticos, sin… … Wikipedia Español
Model checking — Con el nombre Model checking se conoce a un método automático de verificación de un sistema formal, en la mayoría de las ocasiones derivado del hardware o del software de un sistema informático. El sistema es descrito mediante un modelo, que debe … Wikipedia Español
Colación hereditaria — La colación hereditaria ha sido un concepto ampliamente tratado por la más excelsa doctrina, prolijas han sido las tesis doctrinales que, con mayor o menor grado de detalle, han ahondado en su significado. La inefable sutilidad del tema, deviene… … Wikipedia Español
Filtro de cruce — Este artículo o sección sobre tecnología necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 5 de marzo de 2011. También puedes… … Wikipedia Español
Historia de la Provincia de Entre Ríos — Provincia de Entre Ríos. Entre Ríos es una de las 23 provincias que componen la República Argentina. Se halla ubicada al nordeste del país, en donde forma parte de la región mesopotámica. Limita al sur con la Provincia de Buenos Aires, al oeste… … Wikipedia Español
Ética militar — La ética militar es un conjunto de prácticas y discursos que sirven para orientar a las fuerzas armadas y a sus integrantes para que actúen conforme a unos valores y unas normas determinadas, y para mostrar al conjunto de la ciudadanía esos… … Wikipedia Español
Condiciones de trabajo en España — Saltar a navegación, búsqueda … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Reducción de orden

Reducción de orden

Uso

Referencias

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Reducción de orden

Reducción de orden

Uso

Referencias

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo