- Árbol biselado
-
Un Árbol biselado o Árbol Splay es un Árbol binario de búsqueda auto-balanceable, con la propiedad adicional de que a los elementos accedidos recientemente se accederá más rápidamente en accesos posteriores. Realiza operaciones básicas como pueden ser la inserción, la búsqueda y el borrado en un tiempo del orden de O(log n). Para muchas secuencias no uniformes de operaciones, el árbol biselado se comporta mejor que otros árboles de búsqueda, incluso cuando el patrón específico de la secuencia es desconocido. Esta estructura de datos fue inventada por Robert Tarjan y Daniel Sleator.
Todas las operaciones normales de un árbol binario de búsqueda son combinadas con una operación básica, llamada biselación. Esta operación consiste en reorganizar el árbol para un cierto elemento, colocando éste en la raíz. Una manera de hacerlo es realizando primero una búsqueda binaria en el árbol para encontrar el elemento en cuestión y, a continuación, usar rotaciones de árboles de una manera específica para traer el elemento a la cima. Alternativamente, un algoritmo "de arriba a abajo" puede combinar la búsqueda y la reorganización del árbol en una sola fase.
Contenido
Ventajas e inconvenientes
El buen rendimiento de un árbol biselado depende del hecho de que es auto-balanceado, y además se optimiza automáticamente. Los nodos accedidos con más frecuencia se moverán cerca de la raíz donde podrán ser accedidos más rápidamente. Esto es una ventaja para casi todas las aplicaciones, y es particularmente útil para implementar cachés y algoritmos de recolección de basura; sin embargo, es importante apuntar que para un acceso uniforme, el rendimiento de un árbol biselado será considerablemente peor que un árbol de búsqueda binaria balanceado simple.
Los árboles biselados también tienen la ventaja de ser consideradamente más simples de implementar que otros árboles binarios de búsqueda auto-balanceados, como pueden ser los árboles Rojo-Negro o los árboles AVL, mientras que su rendimiento en el caso promedio es igual de eficiente. Además, los árboles biselados no necesitan almacenar ninguna otra información adicional a parte de los propios datos, minimizando de este modo los requerimientos de memoria. Sin embargo, estas estructuras de datos adicionales proporcionan garantías para el peor caso, y pueden ser más eficientes en la práctica para el acceso uniforme.
Uno de los peores casos para el algoritmo básico del árbol biselado es el acceso secuencial a todos los elementos del árbol de forma ordenada. Esto deja el árbol completamente des balanceado (son necesarios n accesos, cada uno de los cuales del orden de O(log n) operaciones). Volviendo a acceder al primer elemento se dispara una operación que toma del orden de O(n) operaciones para volver a balancear el árbol antes de devolver este primer elemento. Esto es un retraso significativo para esa operación final, aunque el rendimiento se amortiza si tenemos en cuenta la secuencia completa, que es del orden de O(log n). Sin embargo, investigaciones recientes muestran que si aleatoriamente volvemos a balancear el árbol podemos evitar este efecto de desbalance y dar un rendimiento similar a otros algoritmos de auto-balanceo.
Al contrario que otros tipos de árboles auto balanceados, los árboles biselados trabajan bien con nodos que contienen claves idénticas. Incluso con claves idénticas, el rendimiento permanece amortizado del orden de O(log n). Todas las operaciones del árbol preservan el orden de los nodos idénticos dentro del árbol, lo cual es una propiedad similar a la estabilidad de los algoritmos de ordenación. Un operación de búsqueda cuidadosamente diseñada puede devolver el nodo más a la izquierda o más a la derecha de una clave dada.
Operaciones
Búsqueda
La búsqueda de un valor de clave en un árbol biselado tiene la característica particular de que modifica la estructura del árbol. El descenso se efectúa de la misma manera que un árbol binario de búsqueda, pero si se encuentra un nodo cuyo valor de clave coincide con el buscado, se realiza una biselación de ese nodo. Si no se encuentra, el nodo biselado será aquel que visitamos por último antes de descartar la búsqueda. Así, la raíz contendrá un sucesor o predecesor del nodo buscado.
Inserción
Es igual que en el árbol binario de búsqueda con la salvedad de que se realiza una biselación sobre el nodo insertado. Además, si el valor de clave a insertar ya existe en el árbol, se bisela el nodo que lo contiene.
Extracción
Esta operación requiere dos biselaciones. Primero se busca el nodo que contiene el valor de clave que se debe extraer. Si no se encuentra, el árbol es biselado en el último nodo examinado y no se realiza ninguna acción adicional. Si se encuentra, el nodo se bisela y se elimina. Con esto el árbol se queda separado en dos mitades, por lo que hay que seleccionar un nodo que haga las veces de raíz. Al ser un árbol binario de búsqueda y estar todos los valores de clave ordenados, podemos elegir como raíz el mayor valor del subárbol izquierdo o el menor valor de clave del derecho.
Operación de Biselación
Esta operación traslada un nodo x, que es el nodo al que se accede, a la raíz . Para realizar esta operación debemos rotar el árbol de forma que en cada rotación el nodo x está más cerca de la raíz. Cada biselación realizada sobre el nodo de interés mantiene el árbol parcialmente equilibrado y además los nodos recientemente accedidos se encuentran en las inmediaciones de la raíz. De esta forma amortizamos el tiempo empleado para realizar la biselación.
Podríamos distinguir 3 casos generales:
-
-
- Caso 1: x es hijo izquierdo o derecho de la raíz, p.
- Caso 2: x es hijo izquierdo de p y este a su vez hijo izquierdo de q o bien ambos son hijos derechos.
- Caso 3: x es hijo izquierdo de p y este a su vez hijo derecho de q o viceversa.
-
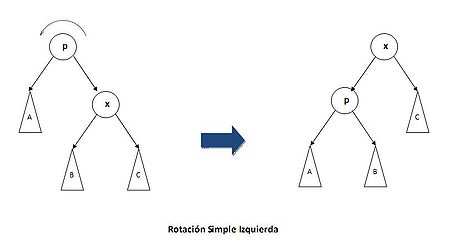
- CASO 1:
Si x es hijo izquierdo de p entonces realizaremos una rotación simple derecha. En caso de que x sea el derecho la rotación que deberemos realizar es simple izquierda.
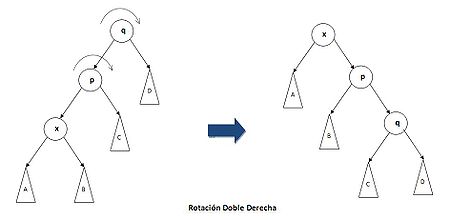
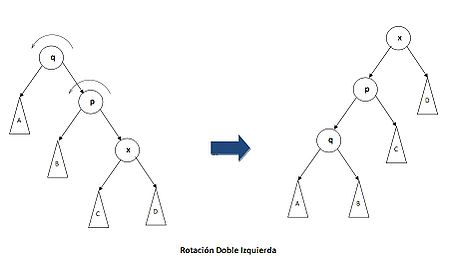
- CASO 2:
Si x es hijo y nieto izquierdo de p y q, respectivamente. Entonces debemos realizar rotación doble a la derecha, en caso de que x sea hijo y nieto derecho de p y q la rotación será doble izquierda.
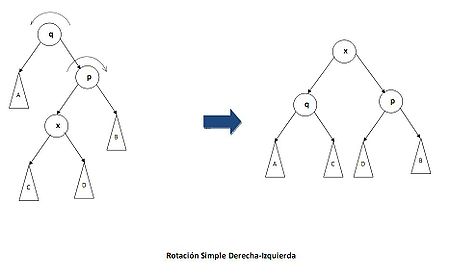
- CASO 3:
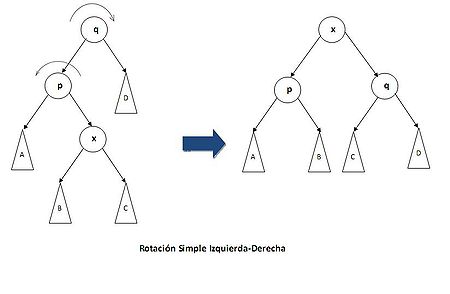
En caso de que x sea hijo izquierdo de p y nieto derecho de q realizaremos una rotación simple derecha en el borde entre x y p y otra simple izquierda entre x y q. En caso contrario, x sea hijo derecho y nieto izquierdo de q, la rotaciones simples será izquierda y después derecha.
Teoremas de rendimiento
Hay muchos teoremas y conjeturas con respecto al peor caso en tiempo de ejecución para realizar una secuencia S de m accesos en un árbol biselado con n elementos.
Teorema del balance
El coste de realizar la secuencia de accesos S es del orden de O(m(logn + 1) + nlogn). En otras palabras, los árboles biselados se comportan tan bien como los árboles de búsqueda binaria con balanceo estático en secuencias de al menos n accesos.
Teorema de optimalidad estática
Sea qi el número de veces que se accede al elemento i en S. El coste de realizar la secuencia de accesos S es del orden de
 . En otras palabras, los árboles biselados se comportan tan bien como los árboles binarios de búsqueda estáticos óptimos en las secuencias de al menos n accesos.
. En otras palabras, los árboles biselados se comportan tan bien como los árboles binarios de búsqueda estáticos óptimos en las secuencias de al menos n accesos.Teorema "Static Finger"
Sea ij el elemento visitado en el j-ésimo acceso de S, y sea f un elemento fijo ("finger"). El coste de realizar la secuencia de accesos S es del orden de

Teorema "Working Set"
Sea t(j) el número de elementos distintos accedidos desde la última vez que se accedió a j antes del instante i. El coste de realizar la secuencia de accesos S es del orden de
 .
.Teorema "Dynamic Finger"
El coste de realizar la secuencia de accesos S es del orden de
 .
.Teorema "Scanning"
También conocido como Teorema de Acceso Secuencial. El acceso a los n elementos de un árbol biselado en orden simétrico es de orden exacto Θ(n), independientemente de la estructura inicial del árbol. El límite superior más ajustado demostrado hasta ahora es 4,5n
Conjetura de optimalidad dinámica
Además del las garantías probadas del rendimiento de los árboles biselados, en el documento original de Sleator y Tarjan hay una conjetura no probada de gran interés. Esta conjetura se conoce como la conjetura de optimalidad dinámica, y básicamente sostiene que los árboles biselados se comportan tan bien como cualquier otro algoritmo de búsqueda en árboles binarios hasta un factor constante.
- Conjetura de optimalidad dinámica: Sea A cualquier algoritmo de búsqueda binaria en árboles que accede a un elemento x atravesando el camino desde la raíz hasta x, a un coste de d(x) + 1, y que entre los accesos puede hacer cualquier rotación en el árbol a un coste de 1 por rotación. Sea A(S) el coste para que A realice la secuencia S de accesos. Entonces el coste de realizar los mismos accesos para un árbol biselado es del orden O(n + A (S)).
Existen varios corolarios de la conjetura de optimalidad dinámica que permanecen sin probar:
- Conjetura Transversal: Sean T1 y T2 dos árboles biselados que contienen los mismos elementos. Sea S la secuencia obtenida tras visitar los elementos de T2 en preorden. El coste total para realizar la secuencia S de accesos en T1 es del orden de O(n).
- Conjetura Deque: Sea S una secuencia de m operaciones de cola doblemente terminada (push, pop, inject, eject). Entonces el coste para la realización de esta secuencia de operaciones S en un árbol biselado es del orden de O(m + n).
- Conjetura Split: Sea S cualquier permutación de los elementos del árbol biselado. Entonces el coste de la eliminación de los elementos en el orden S es del orden de O(n).
Código de ejemplo
/* * SplayTreeApplet: * * The applet demonstrates the Splay Tree. It takes textual commands in a TextArea * and when the user clicks on the Execute button, it processes the commands, updating * the display as it goes. * * @author Hyung-Joon Kim. CSE373, University of Washington. * * Copyrights Note: * This applet is extended from FullHuffmanApplet created by Prof. Steve Tanimoto, * Department of Computer Science and Engineering, University of Washington. * The setup of applet panels and the tree display methods are apprecicatively reused. * */ import javax.swing.*; import java.awt.*; import java.awt.event.*; import java.util.*; public class SplayTreeApplet extends JApplet implements ActionListener, Runnable { ScrolledPanel visPanel; //Donde se pinta el árbol MyScrollPane msp; Button executeButton; Button historyButton; TextArea userInputText; TextArea history; JFrame historyFrame; JTextField statusLine; // La Estructura de datos (árboles biselados) de la clase SplayTree. SplayTree theSplayTree; Font headingFont, treeFont; int topMargin = 40; // Space above top of the tree. int leftMargin = 20; // x value for left side of array. int rightMargin = leftMargin; int yTreeTops = topMargin + 10; // y coord of top of trees. int bottomMargin = 10; // Minimum space betw. bot. of visPanel and bot. of lowest cell. int leftOffset = 5; // space between left side of cell and contents string. int delay = 1500; // default is to wait 1500 ms between updates. Thread displayThread = null; // For SplayTree display: int nodeHeight = 25; // Para dibujar los nodos int nodeWidth = 25; // How wide to plot pink rectangles int nodeVGap = 10; // vertical space between successive nodes int nodeHGap = 10; // horizontal space between successive nodes int nodeHorizSpacing = nodeWidth + nodeHGap; int nodeVertSpacing = nodeHeight + nodeVGap; int interTreeGap = 15; // horizontal space between trees. int ycentering = 3; Color treeColor = new Color(255,255,215); static int m; // variable used when computing columns for tree layouts. public void init() { setSize(700,500); // default size of applet. visPanel = new ScrolledPanel(); visPanel.setPreferredSize(new Dimension(400,400)); msp = new MyScrollPane(visPanel); msp.setPreferredSize(new Dimension(400,200)); Container c = getContentPane(); c.setLayout(new BorderLayout()); c.add(msp, BorderLayout.CENTER); JPanel buttons = new JPanel(); buttons.setLayout(new FlowLayout()); JPanel controls = new JPanel(); controls.setLayout(new BorderLayout()); executeButton = new Button("Execute"); executeButton.addActionListener(this); buttons.add(executeButton); historyButton = new Button("History"); historyButton.addActionListener(this); buttons.add(historyButton); userInputText = new TextArea("\n"); statusLine = new JTextField(); statusLine.setBackground(Color.lightGray); controls.add(buttons, BorderLayout.WEST); controls.add(userInputText, BorderLayout.CENTER); controls.add(statusLine, BorderLayout.SOUTH); controls.setPreferredSize(new Dimension(400,100)); c.add(controls, BorderLayout.SOUTH); c.validate(); theSplayTree = new SplayTree(); // Se crea una instancia de SplayTree headingFont = new Font("Helvetica", Font.PLAIN, 20); treeFont = new Font("Arial", Font.BOLD, 13); history = new TextArea("SplayTreeApplet history:\n", 20, 40); } class ScrolledPanel extends JPanel { public void paintComponent(Graphics g) { super.paintComponent(g); paintTrees(g); } } class MyScrollPane extends JScrollPane { MyScrollPane(JPanel p) { super(p, JScrollPane.VERTICAL_SCROLLBAR_ALWAYS, JScrollPane.HORIZONTAL_SCROLLBAR_ALWAYS); } } public void actionPerformed(ActionEvent e) { if (e.getActionCommand().equals("Execute")) { displayThread = new Thread(this); displayThread.start(); return; } if (e.getActionCommand().equals("History")) { if (historyFrame == null) { historyFrame = new JFrame("History of the SplayTreeApplet"); history.setFont(new Font("Courier", Font.PLAIN, 12)); historyFrame.getContentPane().add(history); historyFrame.setSize(new Dimension(500,500)); } historyFrame.show(); } } // The following is executed by a separate thread for the display. public void run() { String commands = userInputText.getText(); String line = ""; StringTokenizer lines; for (lines = new StringTokenizer(commands, "\n\r\f"); lines.hasMoreTokens();) { line = lines.nextToken(); process(line, lines); } userInputText.setText(""); // Erase all the processed input. } // Helper function called by the run method above: void process(String command, StringTokenizer lines) { String arg1 = ""; String arg2 = ""; StringTokenizer st = new StringTokenizer(command); if (! st.hasMoreTokens()) { return; } String firstToken = st.nextToken(); if (firstToken.startsWith(";")) { return; } history.appendText(command + "\n"); statusLine.setText(command); if (firstToken.equals("RESET")) { theSplayTree = new SplayTree(); updateDisplay(); return; } if (firstToken.equals("DELAY")) { if (st.hasMoreTokens()) { arg1 = st.nextToken(); try { delay = Integer.parseInt(arg1); } catch(NumberFormatException e) { delay = 0; } statusLine.setText("delay = " + delay); } history.appendText("; delay is now " + delay + "\n"); return; } if (firstToken.equals("INSERT")) { arg1 = "UNDEFINED ELEMENT"; if (st.hasMoreTokens()) { arg1 = st.nextToken(); } int data = Integer.parseInt(arg1); if (data < 1 || data > 99) { String msg = "Input NOT valid. Should be between 1-99 integer number."; report(msg); return; } theSplayTree.insert(data); // insert an element checkScrolledPanelSize(); updateDisplay(); if (theSplayTree.statMode) { OldFamilySplayTree fam = theSplayTree.getRoot().oldFam; if (fam != null) { double currentDepth = fam.getFamilyDepth() / (double)fam.numFam; String msg2 = "Current(improved) average depth of old family: " + currentDepth; report(msg2); } } theSplayTree.getRoot().oldFam = null; // reset the old family of the root return; } if (firstToken.equals("FIND")) { arg1 = "UNDEFINED ELEMENT"; if (st.hasMoreTokens()) { arg1 = st.nextToken(); } int data = Integer.parseInt(arg1); String msg = ""; // Check if data is already in the SplayTree and display the result. SplayTree node = theSplayTree.find(data); if ( node == null) { msg = "NOT FOUND: " + data + " is NOT in the Splay Tree"; } else { msg = "FOUND: " + node.element + " is in the Splay Tree."; } report(msg); checkScrolledPanelSize(); updateDisplay(); if (theSplayTree.statMode) { OldFamilySplayTree fam = theSplayTree.getRoot().oldFam; if (fam != null) { double currentDepth = fam.getFamilyDepth() / (double)fam.numFam; String msg2 = "Current(improved) average depth of old family: " + currentDepth; report(msg2); } } theSplayTree.getRoot().oldFam = null; // reset the old family of the root return; } if (firstToken.equals("DELETE")) { arg1 = "UNDEFINED ELEMENT"; if (st.hasMoreTokens()) { arg1 = st.nextToken(); } int data = Integer.parseInt(arg1); theSplayTree.delete(data); // delete an element checkScrolledPanelSize(); updateDisplay(); if (theSplayTree.statMode) { OldFamilySplayTree fam = theSplayTree.getRoot().oldFam; if (fam != null) { double currentDepth = fam.getFamilyDepth() / (double)fam.numFam; String msg2 = "Current(improved) average depth of old family: " + currentDepth; report(msg2); } } theSplayTree.getRoot().oldFam = null; // reset the old family of the root return; } if (firstToken.equals("FIND-MIN")) { SplayTree node = theSplayTree.findMin(theSplayTree.getRoot()); theSplayTree.splay(node); // after find min, splay at the node checkScrolledPanelSize(); updateDisplay(); if (theSplayTree.statMode) { OldFamilySplayTree fam = theSplayTree.getRoot().oldFam; if (fam != null) { double currentDepth = fam.getFamilyDepth() / (double)fam.numFam; String msg2 = "Current(improved) average depth of old family: " + currentDepth; report(msg2); } } theSplayTree.getRoot().oldFam = null; // reset the old family of the root return; } if (firstToken.equals("FIND-MAX")) { SplayTree node = theSplayTree.findMax(theSplayTree.getRoot()); theSplayTree.splay(node); // after find max, splay at the node checkScrolledPanelSize(); updateDisplay(); if (theSplayTree.statMode) { OldFamilySplayTree fam = theSplayTree.getRoot().oldFam; if (fam != null) { double currentDepth = fam.getFamilyDepth() / (double)fam.numFam; String msg2 = "Current(improved) average depth of old family: " + currentDepth; report(msg2); } } theSplayTree.getRoot().oldFam = null; // reset the old family of the root return; } if (firstToken.equals("STAT-MODE")) { if(delay < 2000) { delay = 2000; } theSplayTree.statMode = true; updateDisplay(); return; } history.appendText("[Unknown Splay Tree command]\n"); statusLine.setText("Unknown Spaly Tree command: " + command); } // Here is a "middleman" method that updates the display waiting with // the current time delay after each repaint request. void updateDisplay() { visPanel.repaint(); if (delay > 0) { try { Thread.sleep(delay); } catch(InterruptedException e) {} } } int getInt(String s) { int n = 1; try { n = Integer.parseInt(s); } catch(Exception e) { n = 1; } return n; } /* The following computes the height of the display area needed by the current * heap, and if it won't fit in the scrolled panel, it enlarges the scrolled panel. */ void checkScrolledPanelSize() { // Compute width needed for trees: int treesWidthNeeded = leftMargin + rightMargin; int treesHeightNeeded = 0; Dimension d = visPanel.getPreferredSize(); int currentHeight = (int) d.getHeight(); int currentWidth = (int) d.getWidth(); treesWidthNeeded += theSplayTree.getRoot().getDisplayWidth(); treesHeightNeeded += Math.max(treesHeightNeeded, theSplayTree.getDisplayHeight() + 2*topMargin); // Enlarge scrolled panel if necessary: int widthNeeded = treesWidthNeeded; int heightNeeded = treesHeightNeeded; if ((heightNeeded > currentHeight) || (widthNeeded > currentWidth)) { visPanel.setPreferredSize(new Dimension( Math.max(currentWidth,widthNeeded), Math.max(currentHeight,heightNeeded))); visPanel.revalidate(); // Adjust the vertical scroll bar. } } /** * Splay Tree Class: * * This inner class is a data structure to be demostrated. Integer numbers are assigned * to the data field of Splay Tree, and each node of Splay Tree has left child, right child, * and parent. When a data is accessed by any operations such as FIND, INSERT, etc, Splay Tree * performs a sequence of self-reconstructing processes, so called 'splay', in order to bring * the most-recently-accessed node to the root of the tree. As a result, the nodes near the most- * recently-accessed node become available for a fast accesss in futre. * * @author Hyung-Joon Kim, CSE373, University of Washington. * */ public class SplayTree { // data members for Splay trees : SplayTree root, leftSubtree, rightSubtree, parentTree; int element = 0; // comparable data member (valid between 1-99); OldFamilySplayTree oldFam; String splayStat = ""; // for stat report when splaying is performed int rotateCount = 0; boolean statMode = false; // The following are used in display layout: int depth; // relative y position of this node in the display int column; // relative x position in display, in units of nodes int maxdepth; // height of tree whose root is this node. int xcenter; // position of center of root relative to left side of tree. int ycenter; /** * Constructor por Defecto: */ SplayTree() { } // no hace nada /** * Constructor: Crea un único nodo con los datos asignados. * @param x comparable data(integer number) */ SplayTree(int x) { element = x; } /** * Comprueba si un nodo del árbol es externo - es decir, el nodo no tiene subarboles, es decir que sea una hoja. * @return true si el nodo es externo, sino false. */ boolean isExternal() { return ((leftSubtree == null) && (rightSubtree == null)); } /** * Comprueba si un nodo es la raíz del árbol Splay * @return true si el nodo es la raíz, sino falso. */ boolean isRoot() { return (parentTree == null); } /** * Asigna un nodo nuevo a la raíz del árbol Splay. * @param root toma el valor de node, que es la nueva raiz. */ void setRoot(SplayTree node) { root = node; } /** * Accede a la raíz del árbol Splay. * @return la raíz del árbol Splay. */ SplayTree getRoot() { return root; } /** * Comprueba si un nodo es el hijo izquierdo de su padre. * @return true si el nodo es el hijo izquierdo de su padre, sino false. */ boolean isLeftSubtree() { return ((parentTree != null) && (parentTree.leftSubtree == this)); } /** * Comprueba si un nodo es el hijo derecho de su padre. * @return true si el nodo es el hijo derechoo de su padre, sino false. */ boolean isRightSubtree() { return ((parentTree != null) && (parentTree.rightSubtree == this)); } /** * Encuentra el valor mínimo de los datos guardados en el Árbol Splay * @param T el nodo que funciona como raíz del árboles (o cualquier subarbol del Árbol Splay). * El valor se busca en el subárbol izquierdo debido a la filosofía de un AB.B * @return un nodo cuyo dato es el valor mínimo en el Árbol Splay. */ SplayTree findMin(SplayTree T) { if (T == null) { return null; } else if (T.leftSubtree == null) { return T; //T es el nodo cuyo elemento es el valor mínimo return findMin(T.leftSubtree); // Encuentra recursivamente en el subárbol izquierdo el valor mínimo. } /** *Buscar el máximo valor de los datos Árbol Splay. *@param T el nodo que funciona como raíz del árboles (o cualquier subarbol del Árbol Splay). * El valor se busca en el subárbol derecho debido a la filosofía de un AB.B * @return un nodo cuyo dato es el valor máximo en el Árbol Splay. */ SplayTree findMax(SplayTree T) { if (T == null) { return null; } else if (T.rightSubtree == null) { return T; // T es el nodo cuyo elemento es el valor máximo } return findMax(T.rightSubtree); // Encuentra recursivamente en el subárbol derecho el valor mínimo. } /** * Encuentra un valor buscado en el árbol secuencialmente. * Si lo encuentra llama al método splay() para ajustar el árbol de tal manera que el nodo visitado quede más cerca de la raíz. * @param element valor a buscar en el Árbol Splay. * @return el nodo, si fue encontrado, en la que se realiza splaying. nulo si no se encuentra. */ SplayTree find(int element) { SplayTree T = root; //Encuentra el valor buscado hasta que el árbol no tenga más subárboles, utilizando las propiedas de un AB.B while (T != null) { if (T.element == element) { // Encontrado break; } else if (T.element > element) { T = T.leftSubtree; } else { T = T.rightSubtree; } } if (T == null) { // No se encontró return null; } else { splay(T); // Se bisela el nodo encontrado return T; } } /** * Inserta un nodo en el árbol Splay. Después de la inserción, el Árbol Splay realiza secuencial * Insert a node into the Splay Tree. After insertion, the Splay Tree performs sequential * self-reconstructing processes, so called splay, in order to bring the inserted node * up to the root of the tree. * @param element comparable data which will be inserted into the Splay Tree. */ void insert(int element) { // Crea un nuevo nodo con el elemento a insertar. SplayTree node = new SplayTree(element); //Si el árbol Splay está vacío, es decir, no tiene raíz, // entonces asigna el nuevo nodo a la raíz del árbol. if (root == null) { root = node; return; // En este caso no se necesita biselar el nodo. } SplayTree parent = null; SplayTree T = root; // Busca la ubicación adecuada para insertar el nodo, utilizando las propiedades de un AB,B. while (T != null) { parent = T; if (T.element == node.element) { // El elemento ya estaba en el Árbol Splay break; } else if (T.element > node.element) { T = T.leftSubtree; } else { T = T.rightSubtree; } } if (node.element == parent.element) { String msg = parent.element + " is already in the Splay Tree."; report(msg); splay(parent); // Se bisela el nodo padre en caso de que sea el nodo que se iba a insertar. return; } //Inserta el nodo en el árbol Splay el la posición que se obtuvo en el while anterior. if (parent.element > node.element) { parent.leftSubtree = node; if (node != null) { node.parentTree = parent; } } else { parent.rightSubtree = node; if (node != null) { node.parentTree = parent; } } splay(node); // Despues de la inserción, se biselado el nodo. } /** * This is a helper method for Delete method. It replaces a node with a new node so that * the new node is connected to the parent of the previous node. Note that it should take * care of the pointers of both direction (parent <-> child). * @param T a node to be replaced. * @param newT a node to replace T. */ void replace(SplayTree T, SplayTree newT) { if (T.isRoot()) { // Update the root of the Splay Tree root = newT; if (newT != null) { newT.parentTree = null; } } else { if (T.isLeftSubtree()) { // Make newT be a new left child of the parent of the previous node, T T.parentTree.leftSubtree = newT; if (newT != null) { // Make newT have the parent of the previous node as a new parent newT.parentTree = T.parentTree; } } else { T.parentTree.rightSubtree = newT; if (newT != null) { newT.parentTree = T.parentTree; } } } } /** * Delete a node from the Splay Tree. When a node is deleted, its subtrees should * be reconnected to the Splay Tree somehow without violating the properties of BST. * If a node with two children is deleted, a node with the minimum-valued element * in the right subtrees replaces the deleted node. It does NOT guarantee the balance * of the Splay Tree. * @param x an element to be deleted from the Splay Tree. */ void delete(int x) { boolean wasRoot = false; SplayTree node = root; // Find the element to be deleted while (node != null) { if (node.element == x) { // Found break; } else if (node.element > x) { node = node.leftSubtree; } else { node = node.rightSubtree; } } if (node == null) { String msg = x + " is NOT in the Splay Tree."; report(msg); } else { wasRoot = node.isRoot(); // Remember whether the node is the root or not // The node has no subtrees, so just replace with null if (node.isExternal()) { replace(node, null); } // The node has at least one child, also the node might be the root else if (node.leftSubtree == null) { // the node has only right child replace(node, node.rightSubtree); } else if (node.rightSubtree == null) { // the node has only left child replace(node, node.leftSubtree); } else { // The node has two children // Get a successive node to replace the node that will be deleted SplayTree newNode = findMin(node.rightSubtree); // Special case: the successive node is actually right child of the node to be deleted // The successive node will carry its own right child when it replace the node. if (newNode == node.rightSubtree) { replace(node, newNode); newNode.leftSubtree = node.leftSubtree; } else { // Now the succesive node should be replaced before it is used // Ensured that it has no left child since it's the minimum of subtrees if (newNode.rightSubtree == null) { replace(newNode, null); } else { // The succesive node has right child to take care of replace(newNode, newNode.rightSubtree); } // Replace the node with the succesive node, updating subtrees as well replace(node, newNode); newNode.leftSubtree = node.leftSubtree; newNode.rightSubtree = node.rightSubtree; } } String msg = x + " is succesively deleted from the Splay Tree."; report(msg); // Finally, splaying at the parent of the deleted node. if (!wasRoot) { splay(node.parentTree); } else { splay(root); } // Delete the node completely node.leftSubtree = null; node.rightSubtree = null; node.parentTree = null; } } /** * Splay a node until it reaches up to the root of the Splay Tree. Depending on the location * of a target node, parent, and grandparent, splaying applies one of Zig, Zig-Zig, or Zig-Zag * rotation at each stage. This method is called when a data is accessed by any operations. * @param T a target node at which splaying is performed. */ void splay(SplayTree T) { // Remember total depth of T's family before splaying // Family consists of parent, sibling, children, but not including T itself // This is to see how the data near the splayed data are improved for faster // accesss in future, after spalying T.oldFam = new OldFamilySplayTree(T); double oldFamDepth = T.oldFam.getFamilyDepth() /(double)T.oldFam.numFam; // Keep splaying until T reaches the root of the Splay Tree while (!T.isRoot()) { SplayTree p = T.parentTree; SplayTree gp = p.parentTree; // T has a parent, but no grandparent if (gp == null) { splayStat = splayStat + "Zig "; if (T.isLeftSubtree()) { splayStat = splayStat + "from Left. "; } else { splayStat = splayStat + "from Right. "; } rotation(T); // Zig rotation rotateCount++; } else { // T has both parent and grandparent if (T.isLeftSubtree() == p.isLeftSubtree()) { // T and its parent are in the same direction: Zig-Zig rotation splayStat = splayStat + "Zig-Zig " ; if (T.isLeftSubtree()) { splayStat = splayStat + "from Left, "; } else { splayStat = splayStat + "from Right, "; } rotation(p); rotation(T); rotateCount++; } else { // T and its parent are NOT in the same direction: Zig-Zag rotation splayStat = splayStat + "Zig-Zag "; if (T.isRightSubtree()) { splayStat = splayStat + "from Left, "; } else { splayStat = splayStat + "from Right, "; } rotation(T); rotation(T); rotateCount++; } } } // Report additional statistics of rotations if (statMode) { String stat = "Sequence of rotations: " + splayStat + "\n" + "; Total number of rotations: " + rotateCount + "\n" + "; Average depth of old family: " + oldFamDepth; report(stat); } splayStat = ""; rotateCount = 0; // after splaying(and reporting), reset the variables } /** * Rotate subtrees of the Splay Tree. It updates subtrees of a grandparent, if exists, for * doulbe rotations, and performs single rotation depending on whether a node is left * child or right child. * @param T a node at which single rotation should be performed. */ void rotation(SplayTree T) { SplayTree p = T.parentTree; SplayTree gp = null; if (p != null) { gp = p.parentTree; } if (!T.isRoot()) { // Remember whether T is originally left child or right child final boolean wasLeft = T.isLeftSubtree(); // T has grandparent if (gp != null) { // Replace subtree of grandparent with T for Double rotations if (gp.leftSubtree == p) { gp.leftSubtree = T; T.parentTree = gp; } else { gp.rightSubtree = T; T.parentTree = gp; } } else { // T has no grandparent, set T to the new root. root = T; T.parentTree = null; } // Rotate from left if (wasLeft) { // Attach T's right child to its parent's left child p.leftSubtree = T.rightSubtree; if (T.rightSubtree != null) { T.rightSubtree.parentTree = p; // update the parent of T's subtree } // Now rotate T, so T's parent becomes T's right child T.rightSubtree = p; if (p != null) { p.parentTree = T; } } else { // Rotate from right // Attach T's left child to its parent's right child p.rightSubtree = T.leftSubtree; if (T.leftSubtree != null) { T.leftSubtree.parentTree = p; // update the parent of T's subtree } // Now rotate T, so T's parent becomes T's left child T.leftSubtree = p; if (p != null) { p.parentTree = T; } } } } /** * Self painting method. * @param g graphic object * @param xpos x-cordinate of a node in cartesian plane * @param ypos y-cordinate of a node in cartesian plane */ void paint(Graphics g, int xpos, int ypos) { treeColumns(); paintHelper(g, xpos, ypos); } /** * Actually paint the tree by drawing line, node(circle), and data(integer) * @param g graphic object * @param xpos x-cordinate of a node in cartesian plane * @param ypos y-cordinate of a node in cartesian plane */ void paintHelper(Graphics g, int xpos, int ypos) { String space = ""; if (element < 10) { space = " "; } if (! isExternal()) { g.setColor(Color.blue); if (leftSubtree != null) { g.drawLine(xcenter + xpos - 10, ycenter + ypos, leftSubtree.xcenter + xpos, leftSubtree.ycenter + ypos - 10); } if (rightSubtree != null) { g.drawLine(xcenter + xpos + 10, ycenter + ypos, rightSubtree.xcenter + xpos, rightSubtree.ycenter + ypos - 10); } g.setColor(new Color(102,0,204)); g.fillOval(xpos + column*nodeHorizSpacing -1, ypos + depth*nodeVertSpacing -1, nodeWidth+2, nodeHeight+2); g.setColor(treeColor); g.fillOval(xpos + column*nodeHorizSpacing, ypos + depth*nodeVertSpacing, nodeWidth, nodeHeight); g.setColor(Color.black); } if (isExternal()) { g.setColor(new Color(102,0,204)); g.fillOval(xpos + column*nodeHorizSpacing -1, ypos + depth*nodeVertSpacing -1, nodeWidth+2, nodeHeight+2); g.setColor(treeColor); g.fillOval(xpos + column*nodeHorizSpacing, ypos + depth*nodeVertSpacing, nodeWidth, nodeHeight); g.setColor(Color.black); g.drawString( space + element, xpos + column*nodeHorizSpacing + leftOffset, ypos + depth*nodeVertSpacing + nodeHeight - 8 ); } else { g.drawString(space + element, xpos + column*nodeHorizSpacing + leftOffset, ypos + depth*nodeVertSpacing + nodeHeight - 8); // recursive call to paint subtrees if (leftSubtree != null) { leftSubtree.paintHelper(g, xpos, ypos); } if (rightSubtree != null) { rightSubtree.paintHelper(g, xpos, ypos); } } } /** * Inorder traversal, filling in the depth and the column index of each node * for display purposes. It should also deal with the case where a node has * only one child. * @param currentDepth the current depth of a node * @return the column index of the rightmost node. */ int traverse(int currentDepth) { depth = currentDepth; if (isExternal()) { column = m; m++; maxdepth = depth; } if (leftSubtree == null && rightSubtree != null) { column = m; m++; } if (leftSubtree != null){ leftSubtree.traverse(depth + 1); column = m; m++; } xcenter = column*nodeHorizSpacing + (nodeWidth / 2); ycenter = depth*nodeVertSpacing + nodeHeight - ycentering; if (rightSubtree != null) { int rm = rightSubtree.traverse(depth + 1); if (leftSubtree == null) { maxdepth = rightSubtree.maxdepth; } else { maxdepth = Math.max(leftSubtree.maxdepth, rightSubtree.maxdepth); } return rm; } else { return column; } } /** * Determine total column index of each node, filling a column index of * each node for display purpose. * @return total column index of the Splay Tree */ int treeColumns() { m = 0; return traverse(0) + 1; } /** * Determine the height of the Splay Tree * @param T a node that roots the Splay Tree * @return the height of the Splay Tree at the node */ int treeHeight(SplayTree T) { if (T == null) { return -1; } return (1 + Math.max( treeHeight(T.leftSubtree), treeHeight(T.rightSubtree))); } /** * Get the width needed to display the tree * @return the width of the entire Splay Tree */ int getDisplayWidth() { int hGap = nodeHorizSpacing - nodeWidth; int val = treeColumns() * (nodeHorizSpacing) - hGap; return val; } /** * Get the height needed to display the tree * @return the height of the entire Splay Tree */ int getDisplayHeight() { int maxHeight = treeHeight(root); int val = (maxHeight+1)* nodeVertSpacing - nodeVGap; return val; } } //////////////////// End of SplayTree class ///////////////////// /** * OldFamilySplayTree Class: * * This inner class is to store old family members of a splayed node. * Therefore, after splaying, we can track the old family of the new root * and calculate the relative improvement in terms of depth. After splaying, * the most-recently-accessed data becomes available for O(1) access in the * next time. In addition, all family members also improve the access time * in future. This is a simple way to compare the cost of access to those * family memembers before splaying and after splaying. * * @author Hyung-Joon Kim * */ public class OldFamilySplayTree { // Family members of a node which will be splayed SplayTree oldParent, oldSibling, oldLeftChild, oldRightChild; int numFam; // Numbers of family members /** * Default Constructor: * @param T a node which will be splayed and needs to create old family of it */ OldFamilySplayTree(SplayTree T) { if (T.parentTree != null) { oldParent = T.parentTree; numFam++; } if (T.leftSubtree != null) { oldLeftChild = T.leftSubtree; numFam++; } if (T.rightSubtree != null) { oldRightChild = T.rightSubtree; numFam++; } if (T.isLeftSubtree()) { if (T.parentTree != null && T.parentTree.rightSubtree != null) { oldSibling = T.parentTree.rightSubtree; numFam++; } } else { if (T.parentTree != null && T.parentTree.leftSubtree != null) { oldSibling = T.parentTree.leftSubtree; numFam++; } } } /** * Calculate the average depth of all family member nodes. * This method can calculate the depth before splaying by being called * in the SPLAY method, and the depth after splaying by being called * after repaiting the tree since the depth will is updated in the * PAINT method. * @return the average depth of all family member nodes. */ double getFamilyDepth() { double famDepth = 0.0; if (oldParent != null) { famDepth = famDepth + (double)oldParent.depth; } if (oldSibling != null) { famDepth = famDepth + (double)oldSibling.depth; } if (oldLeftChild != null) { famDepth = famDepth + (double)oldLeftChild.depth; } if (oldRightChild != null) { famDepth = famDepth + (double)oldRightChild.depth; } return famDepth; } } //////////////////// End of OldFamilySplayTree class ///////////////////// // Paint the Splay tree in a left-to-right sequence of trees. void paintTrees(Graphics g) { g.setFont(treeFont); int ystart = yTreeTops; int ypos = ystart; int xpos = leftMargin; g.setFont(headingFont); g.drawString("Splay Tree Demonstration :", xpos, yTreeTops - 20); if (theSplayTree.getRoot() != null) { g.setFont(treeFont); theSplayTree.getRoot().paint(g,xpos,ypos); xpos += interTreeGap; xpos += theSplayTree.getRoot().getDisplayWidth(); } } /* A handy function that reports a message to both the * status line of the applet and the history window. * Multiline messages are not fully visible in the status line. */ void report(String message) { statusLine.setText(message); history.appendText("; " + message + "\n"); } } // Recuerden que es un applet
Véase también
- Árbol (estructura de datos)
- Árbol binario
- Árbol binario de búsqueda
- Árbol AVL
- Árbol rojo-negro
- Árbol multirrama
Enlaces externos
Algoritmo
Implementaciones
Categoría:- Árboles (estructura)
-
Wikimedia foundation. 2010.