- Árbol binario de búsqueda
-
Un árbol binario de búsqueda es un tipo particular de árbol binario que presenta una estructura de datos en forma de árbol usada en informática.
Contenido
Descripción
Un árbol binario de búsqueda (ABB) es un árbol binario definido de la siguiente forma:
Todo árbol vacío es un árbol binario de búsqueda. Un árbol binario no vacío, de raíz R, es un árbol binario de búsqueda si: • En caso de tener subárbol izquierdo, la raíz R debe ser mayor que el valor máximo almacenado en el subárbol izquierdo, y que el subárbol izquierdo sea un árbol binario de búsqueda. • En caso de tener subárbol derecho, la raíz R debe ser menor que el valor mínimo almacenado en el subárbol derecho, y que el subárbol derecho sea un árbol binario de búsqueda.
Para una fácil comprensión queda resumido en que es un árbol binario que cumple que el subárbol izquierdo de cualquier nodo (si no está vacío) contiene valores menores que el que contiene dicho nodo, y el subárbol derecho (si no está vacío) contiene valores mayores.
Para estas definiciones se considera que hay una relación de orden establecida entre los elementos de los nodos. Que cierta relación esté definida, o no, depende de cada lenguaje de programación. De aquí se deduce que puede haber distintos árboles binarios de búsqueda para un mismo conjunto de elementos.
La altura h en el peor de los casos siempre el mismo tamaño que el número de elementos disponibles. Y en el mejor de los casos viene dada por la expresión h = ceil(log2(c + 1)), donde ceil indica redondeo por exceso.
El interés de los árboles binarios de búsqueda (ABB) radica en que su recorrido en inorden proporciona los elementos ordenados de forma ascendente y en que la búsqueda de algún elemento suele ser muy eficiente.
Dependiendo de las necesidades del usuario que trate con una estructura de este tipo se podrá permitir la igualdad estricta en alguno, en ninguno o en ambos de los subárboles que penden de la raíz. Permitir el uso de la igualdad provoca la aparición de valores dobles y hace la búsqueda más compleja.
Un árbol binario de búsqueda no deja de ser un caso particular de árbol binario, así usando la siguiente especificación de árbol binario en maude:
fmod ARBOL-BINARIO {X :: TRIV}is sorts ArbolBinNV{X} ArbolBin{X} . subsort ArbolBinNV{X} < ArbolBin{X} . *** generadores op crear : -> ArbolBin{X} [ctor] . op arbolBin : X$Elt ArbolBin{X} ArbolBin{X} -> ArbolBinNV{X} [ctor] . endfmpodemos hacer la siguiente definición para un árbol binario de búsqueda (también en maude):
fmod ARBOL-BINARIO-BUSQUEDA {X :: ORDEN} is protecting ARBOL-BINARIO{VOrden}{X} . sorts ABB{X} ABBNV{X} . subsort ABBNV{X} < ABB{X} . subsort ABB{X} < ArbolBin{VOrden}{X} . subsort ABBNV{X} < ArbolBinNV{VOrden}{X} . *** generadores op crear : -> ArbolBin{X} [ctor] . op arbolBin : X$Elt ArbolBin{X} ArbolBin{X} -> ArbolBinNV{X} [ctor] . endfmcon la siguiente teoría de orden:
fth ORDEN is protecting BOOL . sort Elt . *** operaciones op _<_ : Elt Elt -> Bool . endfthpara que un árbol binario pertenezca al tipo árbol binario de búsqueda debe cumplir la condición de ordenación siguiente que iría junto al módulo ARBOL-BINARIO-BUSQUEDA:
var R : X$Elt . vars INV DNV : ABBNV{X} . vars I D : ABB{X} . mb crear : ABB{X} . mb arbolBin(R, crear, crear) : ABBNV{X} . cmb arbolBin(R, INV, crear) : ABBNV{X} if R > max(INV) . cmb arbolBin(R, crear, DNV) : ABBNV{X} if R < min(DNV) . cmb arbolBin(R, INV, DNV) : ABBNV{X} if (R > max(INV)) and (R < min(DNV)) . ops min max : ABBNV{X} -> X$Elt . eq min(arbolBin(R, crear, D)) = R . eq min(arbolBin(R, INV, D)) = min(INV) . eq max(arbolBin(R, I, crear)) = R . eq max(arbolBin(R, I, DNV)) = max(DNV) .Operaciones
Todas las operaciones realizadas sobre árboles binarios de búsqueda están basadas en la comparación de los elementos o clave de los mismos, por lo que es necesaria una subrutina, que puede estar predefinida en el lenguaje de programación, que los compare y pueda establecer una relación de orden entre ellos, es decir, que dados dos elementos sea capaz de reconocer cual es mayor y cual menor. Se habla de clave de un elemento porque en la mayoría de los casos el contenido de los nodos será otro tipo de estructura y es necesario que la comparación se haga sobre algún campo al que se denomina clave.
Búsqueda
La búsqueda consiste acceder a la raíz del árbol, si el elemento a localizar coincide con éste la búsqueda ha concluido con éxito, si el elemento es menor se busca en el subárbol izquierdo y si es mayor en el derecho. Si se alcanza un nodo hoja y el elemento no ha sido encontrado se supone que no existe en el árbol. Cabe destacar que la búsqueda en este tipo de árboles es muy eficiente, representa una función logarítmica. El maximo número de comparaciones que necesitaríamos para saber si un elemento se encuentra en un árbol binario de búsqueda estaría entre [log2(N+1)] y N, siendo N el número de nodos. La búsqueda de un elemento en un ABB (Árbol Binario de Búsqueda) se puede realizar de dos formas, iterativa o recursiva.
Ejemplo de versión iterativa en el lenguaje de programación C, suponiendo que estamos buscando una clave alojada en un nodo donde está el correspondiente "dato" que precisamos encontrar:
data Buscar_ABB(abb t,clave k) { abb p; dato e; e=NULL; p=t; if (!estaVacio(p)) { while (!estaVacio(p) && (p->k!=k) ) { if (k < p->k) { p=p->l; } if (p->k < k) { p=p->r; } } if (!estaVacio(p) &&(p->d!=NULL) ) { e=copiaDato(p->d); } } return e; }
Véase ahora la versión recursiva en ese mismo lenguaje:
int buscar(tArbol *a, int elem) { if (a == NULL) return 0; else if (a->clave < elem) return buscar(a->hDerecho, elem); else if (a->clave > elem) return buscar(a->hIzquierdo, elem); else return 1; }
Otro ejemplo en Python:
def search_binary_tree(node, key): if node is None: return None # not found if key < node.key: return search_binary_tree(node.left, key) else if key > node.key: return search_binary_tree(node.right, key) else: return node.value
En Pascal:
Function busqueda(T:ABR, y: integer):ABR begin if (T=nil) or (^T.raiz=y) then busqueda:=T; else if (^T.raiz<y) then busqueda:=busqueda(^T.dch,y); else busqueda:=busqueda(^T.izq,y); end;
Una especificación en maude para la operación de búsqueda quedaría de la siguiente forma:
op esta? : X$Elt ABB{X} -> Bool . var R R1 R2 : X$Elt . vars I D : ABB{X} . eq esta?(R, crear) = false . eq esta?(R1, arbolBin(R2, I, D)) = if R1 == R2 then true else if R1 < R2 then esta?(R1, I) else esta?(R1, D) fi fi .Inserción
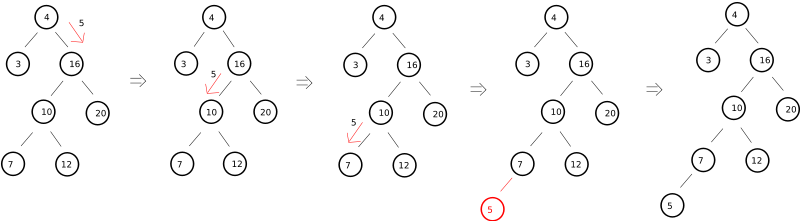
La inserción es similar a la búsqueda y se puede dar una solución tanto iterativa como recursiva. Si tenemos inicialmente como parámetro un árbol vacío se crea un nuevo nodo como único contenido el elemento a insertar. Si no lo está, se comprueba si el elemento dado es menor que la raíz del árbol inicial con lo que se inserta en el subárbol izquierdo y si es mayor se inserta en el subárbol derecho. De esta forma las inserciones se hacen en las hojas.
Como en el caso de la búsqueda puede haber varias variantes a la hora de implementar la inserción en el TAD (Tipo Abstracto de Datos), y es la decisión a tomar cuando el elemento (o clave del elemento) a insertar ya se encuentra en el árbol, puede que éste sea modificado o que sea ignorada la inserción. Es obvio que esta operación modifica el ABB perdiendo la versión anterior del mismo.
A continuación se muestran las dos versiones del algoritmo en pseudolenguaje, iterativa y recursiva, respectivamente.
PROC InsertarABB(árbol:TABB; dato:TElemento) VARIABLES nuevonodo,pav,pret:TABB clavenueva:Tclave ele:TElemento INICIO nuevonodo <- NUEVO(TNodoABB) nuevonodo^.izq <- NULO nuevonodo^.der <- NULO nuevonodo^.elem <- dato SI ABBVacío (árbol) ENTONCES árbol <- nuevonodo ENOTROCASO clavenueva <- dato.clave pav <- árbol // Puntero Avanzado pret <- NULO // Puntero Retrasado MIENTRAS (pav <- NULO) HACER pret <- pav ele = pav^.elem SI (clavenueva < ele.clave ) ENTONCES pav <- pav^.izq EN OTRO CASO pav <- pav^.dch FINSI FINMIENTRAS ele = pret^.elem SI (clavenueva < ele.clave ) ENTONCES pret^.izq <- nuevonodo EN OTRO CASO pret^.dch <- nuevonodo FINSI FINSI FINPROC InsertarABB(árbol:TABB; dato:TElemento) VARIABLES ele:TElemento INICIO SI (ABBVacío(árbol)) ENTONCES árbol <- NUEVO(TNodoABB) árbol^.izq <- NULO árbol^.der <- NULO árbol^.elem <- dato EN OTRO CASO ele = InfoABB(árbol) SI (dato.clave < ele.clave) ENTONCES InsertarABB(árbol^.izq, dato) EN OTRO CASO InsertarABB(árbol^.dch, dato) FINSI FINSI FINSe ha podido apreciar la simplicidad que ofrece la versión recursiva, este algoritmo es la traducción en C. El árbol es pasado por referencia para que los nuevos enlaces a los subárboles mantengan la coherencia.
void insertar(tArbol **a, int elem) { if (*a == NULL) { *a = (tArbol *) malloc(sizeof(tArbol)); (*a)->clave = elem; (*a)->hIzquierdo = NULL; (*a)->hDerecho = NULL; } else if ((*a)->clave < elem) insertar(&(*a)->hDerecho, elem); else if ((*a)->clave > elem) insertar(&(*a)->hIzquierdo, elem); }
Ejemplo en Python:
def binary_tree_insert(node, key, value): if node is None: return TreeNode(None, key, value, None) if key == node.key: return TreeNode(node.left, key, value, node.right) if key < node.key: return TreeNode(binary_tree_insert(node.left, key, value), node.key, node.value, node.right) else: return TreeNode(node.left, node.key, node.value, binary_tree_insert(node.right, key, value))
Otro ejemplo en Pascal:
Procedure Insercion(var T:ABR, y:integer) var ultimo:ABR; actual:ABR; nuevo:ABR; begin ultimo:=nil; actual:=T; while (actual<>nil) do begin ultimo:=actual; if (^actual.raiz<y) then actual:=^actual.dch; else actual:=^actual.izq; end; new(nuevo); ^nuevo.raiz:=y; ^nuevo.izq:=nil; ^nuevo.dch:=nil; if ultimo=nil then T:=nuevo; else if ^ultimo.raiz<y then ^ultimo.dch:=nuovo; else ^ultimo.izq:=nuevo; end;
Véase también un ejemplo de algoritmo recursivo de inserción en un ABB en el lenguaje de programación Maude:
op insertar : X$Elt ABB{X} -> ABBNV{X} . var R R1 R2 : X$Elt . vars I D : ABB{X} . eq insertar(R, crear) = arbolBin(R, crear, crear) . eq insertar(R1, arbolBin(R2, I, D)) = if R1 < R2 then arbolBin(R2, insertar(R1, I), D) else arbolBin(R2, I, insertar(R1, D)) fi .La operación de inserción requiere, en el peor de los casos, un tiempo proporcional a la altura del árbol.
Borrado
La operación de borrado no es tan sencilla como las de búsqueda e inserción. Existen varios casos a tener en consideración:
- Borrar un nodo sin hijos ó nodo hoja: simplemente se borra y se establece a nulo el apuntador de su padre.
 Nodo a eliminar 74
Nodo a eliminar 74- Borrar un nodo con un subárbol hijo: se borra el nodo y se asigna su subárbol hijo como subárbol de su padre.
 Nodo a eliminar 70
Nodo a eliminar 70- Borrar un nodo con dos subárboles hijo: la solución está en reemplazar el valor del nodo por el de su predecesor o por el de su sucesor en inorden y posteriormente borrar este nodo. Su predecesor en inorden será el nodo más a la derecha de su subárbol izquierdo (mayor nodo del subarbol izquierdo), y su sucesor el nodo más a la izquierda de su subárbol derecho (menor nodo del subarbol derecho). En la siguiente figura se muestra cómo existe la posibilidad de realizar cualquiera de ambos reemplazos:
 Nodo a eliminar 59
Nodo a eliminar 59El siguiente algoritmo en C realiza el borrado en un ABB. El procedimiento reemplazar busca la mayor clave del subárbol izquierdo y la asigna al nodo a eliminar.
void borrar(tArbol **a, int elem) { void reemplazar(tArbol **a, tArbol **aux); tArbol *aux; if (*a == NULL) return; if ((*a)->clave < elem) borrar(&(*a)->hDerecho, elem); else if ((*a)->clave > elem) borrar(&(*a)->hIzquierdo, elem); else if ((*a)->clave == elem) { aux = *a; if ((*a)->hIzquierdo == NULL) *a = (*a)->hDerecho; else if ((*a)->hDerecho == NULL) *a = (*a)->hIzquierdo; else reemplazar(&(*a)->hIzquierdo, &aux); free(aux); } } void reemplazar(tArbol **a, tArbol **aux) { if ((*a)->hDerecho == NULL) { (*aux)->clave = (*a)->clave; *aux = *a; *a = (*a)->hIzquierdo; } else reemplazar(&(*a)->hDerecho, aux); }
Otro ejemplo en Pascal.
Procedure Borrar(var T:ABR, x:ABR) var aBorrar:ABR; anterior:ABR; actual:ABR; hijo:ABR; begin if (^x.izq=nil) or (^x.dch=nil) then aBorrar:=x; else aBorrar:=sucesor(T,x); actual:=T; anterior:=nil; while (actual<>aBorrar) do begin anterior:=actual; if (^actual.raiz<^aBorrar.raiz) then actual:=^actual.dch; else actual:=^actual.izq; end; if (^actual.izq=nil) then hijo:=^actual.dch; else hijo:=^actual.izq; if (anterior=nil) then T:=hijo; else if (^anterior.raiz<^actual.raiz) then ^anterior.dch:=hijo; else ^anterior.izq:=hijo; if (aBorrar<>x) then ^x.raiz:=^aBorrar.raiz; free(aBorrar); end;
Véase también un ejemplo de algoritmo recursivo de borrado en un ABB en el lenguaje de programación Maude, considerando los generadores crear y arbolBin. Esta especificación hace uso de la componente clave a partir de la cual se ordena el árbol.
op eliminar : X$Elt ABB{X} -> ABB{X} . varS R M : X$Elt . vars I D : ABB{X} . vars INV DNV : ABBNV{X} . ops max min : ArbolBin{X} -> X$Elt . eq min(arbolBin(R, crear, D)) = R . eq max(arbolBin(R, I, crear)) = R . eq min(arbolBin(R, INV, D)) = min(INV) . eq max(arbolBin(R, I, DNV )) = max(DNV) . eq eliminar(M, crear) = crear . ceq eliminar(M, arbolBin(R, crear, D)) = D if M == clave(R) . ceq eliminar(M, arbolBin(R, I, crear)) = I if M == clave(R) . ceq eliminar(M, arbolBin(R, INV, DNV)) = arbolBin(max(INV), eliminar(clave(max(INV)), INV), DNV) if M == clave(R) . ceq eliminar(M, arbolBin(R, I, D)) = arbolBin(R, eliminar(M, I), D) if M < clave(R) . ceq eliminar(M, arbolBin(R, I, D)) = arbolBin(R, I, eliminar(M, D)) if clave(R) < M .Otras Operaciones
Otra operación sería por ejemplo comprobar que un árbol binario es un árbol binario de búsqueda. Su implementación en maude es la siguiente:
op esABB? : ABB{X} -> Bool . var R : X$Elt . vars I D : ABB{X} . eq esABB?(crear) = true . eq esABB?(arbolbBin(R, I, D)) = (Max(I) < R) and (Min(D) > R) and (esABB?(I)) and (esABB?(D)) .Recorridos
Se puede hacer un recorrido de un árbol en profundidad o en anchura.
Los recorridos en anchura son por niveles, se realiza horizontalmente desde la raíz a todos los hijos antes de pasar a la descendencia de alguno de los hijos.
El recorrido en profundidad lleva al camino desde la raíz hacia el descendiente más lejano del primer hijo y luego continúa con el siguiente hijo. Como recorridos en profundidad tenemos inorden, preorden y postorden.
Una propiedad de los ABB es que al hacer un recorrido en profundidad inorden obtenemos los elementos ordenados de forma ascendente.
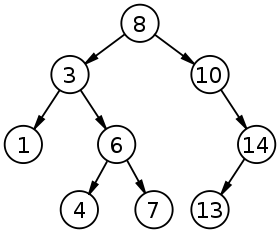
 Ejemplo árbol binario de búsqueda
Ejemplo árbol binario de búsquedaResultado de hacer el recorrido en:
Inorden = [6, 9, 13, 14, 15, 17, 20, 26, 64, 72].
Preorden = [15, 9, 6, 14, 13, 20, 17, 64, 26, 72].
Postorden =[6, 13, 14, 9, 17, 26, 72, 64, 20, 15].
Recorridos en Visual Basic .Net'funcion de recorrido en PREORDEN Public Function preorden() As String cadenasalida = "" rePreorden(raiz) Return cadenasalida End Function Private Sub rePreorden(ByVal padre As Nodo) If IsNothing(padre) Then Return End If cadenasalida = cadenasalida & "-" & padre.dato rePreorden(padre.ant) rePreorden(padre.sig) End Sub'funcion de recorrido en POSTORDEN Public Function postorden() As String cadenasalida = "" reposorden(raiz) Return cadenasalida End Function Private Sub repostorden(ByVal padre As Nodo) If IsNothing(padre) Then Return End If repostorden(padre.ant) repostorden(padre.sig) cadenasalida = cadenasalida & "-" & padre.dato End Sub'funcion de recorrido en INORDEN Public Function inorden() As String cadenasalida = "" reinorden(raiz) Return cadenasalida End Function Private Sub reinorden(ByVal padre As Nodo) If IsNothing(padre) Then Return End If reinorden(padre.ant) cadenasalida = cadenasalida & "-" & padre.dato reinorden(padre.sig) End SubTipos de árboles binarios de búsqueda
Hay varios tipos de árboles binarios de búsqueda. Los árboles AVL, árbol rojo-negro, son árboles autobalanceables . Los árbol biselado son árboles también autobalanceables con la propiedad de que los elementos accedidos recientemente se accederá más rápido en posteriores accesos. En el montículo como en todos los árboles binarios de búsqueda cada nodo padre tiene un valor mayor q sus hijos y además es completo, esto es cuando todos los niveles están llenos con excepción del último que puede no estarlo.
Hay muchos tipos de árboles binarios de búsqueda. Los árboles AVL y los árbol rojo-negro son ambos formas de árboles binarios de búsqueda autobalanceables. Un árbol biselado es un árbol binario de búsqueda que automáticamente mueve los elementos a los que se accede frecuentemente cerca de la raíz. En los montículos, cada nodo también mantiene una prioridad y un nodo padre tiene mayor prioridad que su hijo.
Otras dos maneras de configurar un árbol binario de búsqueda podría ser como un árbol completo o degenerado.
Un árbol completo es un árbol con "n" niveles, donde cada nivel d <= n-1; el número de nodos existentes en el nivel "d" es igual que 2d. Esto significa que todos los posibles nodos existen en esos niveles, no hay ningún hueco. Un requirimiento adicional para un árbol binario completo es que para el nivel "n", los nodos deben estar ocupados de izquierda a derecha, no pudiendo haber un hueco a la izquierda de un nodo ocupado.
Un árbol degenerativo es un árbol que, para cada nodo padre, sólo hay asociado un nodo hijo. Por lo que se comporta como una lista enlazada.
Comparación de rendimiento
D. A. Heger(2004)[1] realiza una comparación entre los diferentes tipos de árboles binarios de búsqueda para encontrar que tipo nos daría el mejor rendimiento para cada caso. Los montículos se encuentran como el tipo de árbol binario de búsqueda que mejor resultado promedio da, mientras que los árboles rojo-negro los que menor rendimiento medio nos aporta.
Buscando el Árbol binario de búsqueda óptimo
Si nosotros no tenemos en mente planificar un árbol binario de búsqueda, y sabemos exactamente como de frecuente serán visitados cada elemento podemos construir un árbol binario de búsqueda óptimo con lo que conseguiremos que la media de gasto generado a la hora de buscar un elemento sea minimizado.
Asumiendo que conocemos los elementos y en qué nivel está cada uno, también conocemos la proporción de futuras búsquedas que se harán para encontrar dicho elemento. Si es así, podemos usar una solución basada en la programación dinámica.
En cambio, a veces sólo tenemos la estimación de los costes de búsqueda, como pasa con los sistemas que nos muestra el tiempo que ha necesitado para realizar una búsqueda. Un ejemplo, si tenemos un ABB de palabras usado en un corrector ortográfico, deberíamos balancear el árbol basado en la frecuencia que tiene una palabra en el Corpus lingüístico, desplazando palabras como "de" cerca de la raíz y palabras como "vesánico" cerca de las hojas. Un árbol como tal podría ser comparado con los árboles Huffman que tratan de encontrar elementos que son accedidos frecuentemente cerca de la raíz para producir una densa información; de todas maneras, los árboles Huffman sólo puede guardar elementos que contienen datos en las hojas y estos elementos no necesitan ser ordenados.
En cambio, si no sabemos la secuencia en la que los elementos del árbol van a ser accedidos, podemos usar árboles biselados que son tan buenos como cualquier árbol de búsqueda que podemos construir para cualquier secuencia en particular de operaciones de búsqueda.
Árboles alfabéticos son árboles Huffman con una restricción de orden adicional, o lo que es lo mismo, árboles de búsqueda con modificación tal que todos los elementos son almacenados en las hojas.
Véase también
- Árbol (programación)
- Árbol Binario
- Árbol AVL
- Árbol 2-3
- Árbol B
- Árbol Rojo-Negro
- Árbol Splay
- Árbol Multirrama
Referencias
- ↑ Heger, Dominique A. (2004), «A Disquisition on The Performance Behavior of Binary Search Tree Data Structures», European Journal for the Informatics Professional 5 (5), http://www.upgrade-cepis.org/issues/2004/5/up5-5Mosaic.pdf
Enlaces externos
Categoría:- Árboles (estructura)
Wikimedia foundation. 2010.