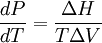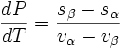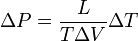- Relación de Clausius-Clapeyron
-
Relación de Clausius-Clapeyron
En termoquímica, la relación de Clausius-Clapeyron es una manera de caracterizar la transición de fase entre dos estados de la materia, como el líquido y el sólido. En un diagrama P-T (presión-temperatura), la línea que separa ambos estados se conoce como curva de coexistencia. La relación de Clausius-Clapeyron da la pendiente de dicha curva. Matemáticamente se puede expresar como:
donde
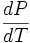es la pendiente de dicha curva, ΔH es el calor latente o entalpía del cambio de fase y ΔV es el volumen.Derivación
Supongamos dos fases, α y β, en contacto y en equilibrio ambas. Los potenciales químicos se relacionan según μα = μβ. A lo largo de la curva de coexistencia, tenemos que dμα = dμβ. Usando la relación de Gibbs-Duhem dμ = − sdT + vdP donde s y v son, respectivamente, la entropía y el volumen por partícula, obtenemos:
- (sβ − sα)dT + (vα − vβ)dP = 0
Reordenamos la expresión y obtenemos
De la relación entre el cambio de calor y entropía en un proceso reversible δQ = TdS, tenemos que la cantidad de calor añadido en la reacción es
- L = T(sα − sβ)
...y combinando las dos últimas ecuaciones obtenemos la relación estándar.
Aplicación
Esta ecuación puede ser usada para predecir dónde se va a dar una transición de fase. Por ejemplo, la relación de Clausius-Clapeyron se usa frecuentemente para explicar el patinaje sobre hielo: el patinador, con la presión de sus cuchillas, aumenta localmente la presión sobre el hielo, lo cual lleva a éste a fundirse. ¿Funciona dicha explicación? Si T=−2 ºC, podemos emplear la ecuación de Clausius-Clapeyron para ver qué presión es necesaria para fundir el hielo a dicha temperatura. Asumimos que
y sustituyendo en
L = 3.34·105 J/kg,
T=293K,
ΔV = -9.05·10-5 m3/kg,
y
- ΔT = 2K,
obtenemos
- ΔP = 27,2 MPa
Esta presión es la equivalente a la de un peso de 150 kg (luchador de sumo) situado sobre unos patines de área total de contacto con el hielo de 0,5 cm². Evidentemente, éste no es el mecanismo por el cual se funde el hielo bajo las cuchillas de los patines (es un efecto de calentamiento por fricción).
-
- La ecuación aplicada no es correcta y por tanto tampoco su conclusión. Véase la discusión para la explicación.
Categorías: Fisicoquímica | Termodinámica
Wikimedia foundation. 2010.
