- Sistema de funciones iteradas
-
Compacto inicial y 6 iteraciones de un IFS formado por 3 aplicaciones contractivas. En la primera iteración el recuadro inicial se hace corresponder con la unión de los recuadros A, B y C.
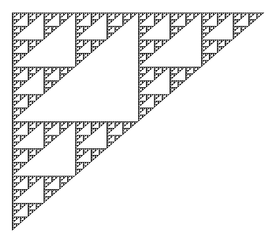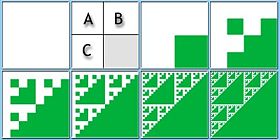
Único punto fijo de la aplicación inducida por el anterior IFS, fractal al que se conoce como triángulo de Sierpinski. Obsérvese que está formado por la unión de 3 copias de sí mismo.En matemáticas, se denomina sistema de funciones iteradas o IFS (acrónimo de la traducción inglesa iterated function system) a un método para la construcción de fractales a partir de la información suministrada por un conjunto finito {f1, ..., fk } de aplicaciones de un espacio métrico completo.
En dicho método, un compacto cualquiera A es sustituido en cada iteración por la unión de sus imágenes bajo cada una de las aplicaciones del IFS:
.
Podemos preguntarnos qué sucede cuando iteramos la acción de la aplicación F. Bajo ciertas condiciones, se demuestra que la sucesión {A. F(A), F(F(A)),...} tiene por límite al único punto fijo de F: un conjunto compacto K al que llamaremos fractal IFS, y técnicamente el atractor del IFS.
La autosimilitud de K, una de las características de los fractales, se deriva de la condición de punto fijo K = F(K), es decir,
,
en la que observamos que K estará formado por unión de k copias de sí mismo, posiblemente deformadas, y de menor tamaño (si las aplicaciones son contractivas), que pueden solaparse o no.
Contenido
Definición formal
- Llamamos sistema de funciones iteradas o IFS a una colección finita
de aplicaciones contractivas de un espacio métrico completo (X.d). Designaremos sus factores de contracción[1] por ci. - Êstas aplicaciones inducen una aplicación
entre las partes de X, definida por 
. Si dotamos a P(X) de la distancia de Hausdorff y nos restringimos a los subconjuntos compactos, F será a su vez una aplicación contractiva sobre un espacio métrico que a su vez es completo, y por tanto tendrá un punto fijo K. Este punto fijo será también el límite de la sucesión {A. F(A), F(F(A)),...}. - Decimos que un compacto no vacío K es un atractor del IFS si satisface:
Observamos que esta condición nos indica que el conjunto es igual a la unión de copias de sí mismo de menor tamaño.
Cálculo de la dimensión fractal
El valor de la dimensión fractal D de un objeto producido por un IFS compuesto de k aplicaciones contractivas de factor de contracción ci, en caso de que estas no provoquen solapamiento, viene dado por la solución de la ecuación
El problema inverso: Teorema del collage
Este teorema nos permite encontrar un IFS cuyo atractor esté todo lo próximo que deseemos (en el sentido de la distancia de Hausdorff) o coincida con un conjunto prefijado C.
Para hallar dicho IFS necesitamos encontrar un número suficiente de aplicaciones contractivas tales que la unión ("collage") de las imágenes del conjunto bajo estas aplicaciones esté lo suficientemente próxima o coincida con el propio conjunto.
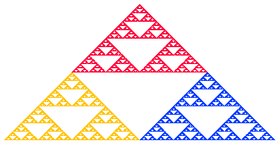
El conjunto C puede expresarse como unión de tres versiones reducidas que llamaremos f1(C), f2(C) y f3(C). Para encontrar el IFS asociado debemos calcular la expresión de las fi.Como ejemplo, para conseguir un IFS cuyo atractor corresponda al conjunto fractal de la figura son necesarias 3 transformaciones:
- La que lleva el conjunto total en el triángulo amarillo:
- La que lleva el conjunto total en el triángulo azul:
- La que lleva el conjunto total en el triángulo rojo:
Algoritmos de representación
Algoritmo determinista
Simplemente construye los sucesivos conjuntos {A, F(A), F(F(A)),...}. Como dicha sucesión converge al atractor del IFS independientemente del conjunto A de partida, puede usarse cualquier valor inicial, con frecuencia una caja cuadrada.
Fractal IFS construido mediante el algoritmo de iteración aleatoria.Algoritmo de iteración aleatoria
En este algoritmo, también llamado "juego del caos", un punto que describe una danza aparentemente aleatoria va perfilando progresivamente la estructura del atractor. Para ello, se elige un punto x0 del espacio métrico y se forma una sucesión del siguiente modo: en cada paso se escoge aleatoriamente y con igual probabilidad
Se demuestra que la sucesión así formada "converge" al atractor del IFS.
Este algoritmo permite una generalización en que se asignan distintas probabilidades pi a la hora de escoger cada fi. Diferentes probabilidades permiten obtener diversas texturas y densidades, útiles para el modelado de escenas naturales. Un IFS en que cada función fi va acompañada de un número positivo pi de modo que
se denomina IFS con probabilidades.Notas
- ↑ También llamados constantes Lipschitz de las funciones.
Bibliografía
- M. Barnsley. Fractals everywhere.Academic Press Inc, 1988. ISBN 0-12-079062-9.
- Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd.. pp. Cap. 9. ISBN 0-470-84862-6.
Categoría:- Fractales
Wikimedia foundation. 2010.
