- Espacio completo
-
Espacio completo
En análisis funcional un espacio métrico X se dice que es completo si toda sucesión de Cauchy converge, es decir, existe un elemento del espacio que es el límite de la sucesión.
La idea intuitiva de este concepto es que no hay nada "pegado" a X y que no esté en X. Así, por ejemplo, la recta real es un espacio completo, pero si le saco un punto, deja de serlo. Del mismo modo, todo intervalo cerrado en los reales es completo, pero todo intervalo acotado y abierto o semi-abierto no lo es. Por ejemplo, el intervalo (0,1) no es completo, pues la sucesión
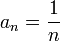es claramente de Cauchy, pero no converge, pues su límite es cero, punto que "no existe", pues no está en el conjunto.La importancia de los espacios completos es que es mucho más fácil demostrar que una sucesión es de Cauchy a que converge, dado que para demostrar que una sucesión es de Cauchy no se necesita conocer el valor al que converge. Una vez demostrada que la sucesión es de Cauchy por la completitud del espacio, se llega a que la sucesión converge. Se ha podido construir en ellos métodos poderosos para demostrar la existencia de soluciones de ecuaciones (v.) numéricas, diferenciales o integrales en determinadas condiciones.
Si un espacio normado es completo con la distancia inducida por su norma, se llama espacio de Banach. Si además la norma está inducida por un producto escalar, se dice que se trata de un espacio de Hilbert.
Ejemplos
- El conjunto de los números racionales,
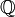, con el valor absoluto como distancia (d(x,y) = abs(x-y))) no es completo dado que existen sucesiones de números racionales que convergen a números irracionales. Debido a la convergencia (en los números reales), dichas sucesiones son de Cauchy, pero el valor límite no es racional por lo que no convergen en los números racionales.
- El conjunto de los números reales,
, es completo con la métrica valor absoluto.
Algunos resultados
- En un espacio métrico toda sucesión convergente es de Cauchy.
- Sea (X,d) un espacio métrico completo y sea Y un subconjunto no vacío de X. Entonces (Y,d) es completo si y sólo si Y es un conjunto cerrado en (X,d).
- Teorema de las esferas encajadas. Sea (X,d) un espacio métrico. Es completo si y sólo si cualquier sucesión de esferas encajadas cuyos radios tiendan a cero tiene intersección no vacía.
- Todo espacio vectorial normado de dimensión finita es completo.
- Todo espacio métrico puede ser completado, esto es, existe otro espacio métrico (Y,d') completo, y una isometría
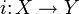, tal que i(X) es un conjunto denso en Y. Así, por ejemplo, la completación del intervalo (0,1) resulta ser el intervalo [0,1], y la completación de los racionales son los reales. - Teorema del punto fijo de Banach o Teorema de la Aplicación contractiva. Sea X un espacio métrico completo, y sea: f : X en X una aplicación contractiva. Entonces, existe un único punto p de X tal que f(p) = p.
Categorías: Topología | Análisis funcional - El conjunto de los números racionales,
Wikimedia foundation. 2010.
