Conjunto de Cantor

Conjunto de Cantor
De izquierda a derecha, sucesivos pasos de la construcción geométrica del conjunto de Cantor. Para ilustrar la definición numérica se destacan cuatro puntos del conjunto (0, 2/3, 1 y 1/4) y su expresión en base 3.

El conjunto de Cantor, llamado así por ser introducido por Georg Cantor[1] en 1883, es un destacado subconjunto fractal del intervalo real [0, 1], que admite dos definiciones equivalentes:

  • la definición numérica: es el conjunto de todos los puntos del intervalo real [0,1] que admiten una expresión en base 3 que no utilice el dígito 1.
  • la definición geométrica, de carácter recursivo, que elimina en cada paso el segmento abierto correspondiente al tercio central de cada intervalo.

Además de una curiosidad matemática, contradice una intuición relativa al tamaño de objetos geométricos: es un conjunto de medida nula, pero no es vacío ni numerable.

Lo que Cantor no sabía era que este conjunto ya había sido descubierto en 1875 por un matemático dublinés, Henry John Stephen Smith (1826-1883). Pero como Smith falleció y su descubrimiento era prácticamente desconocido, fue Cantor el que quedo asociado a este conjunto.[2]

Contenido

Construcción geométrica

Se construye de modo recursivo dando los siguientes pasos:

  • El primer paso es tomar el intervalo [0, 1].
  • El segundo paso es quitarle su tercio interior, es decir el intervalo abierto (1/3; 2/3).
  • El tercero es quitar a los dos segmentos restantes sus respectivos tercios interiores, es decir los intervalos abiertos (1/9; 2/9) y (7/9; 8/9).
  • Los pasos siguientes son idénticos: quitar el tercio de todos los intervalos que quedan. El proceso no tiene fin.

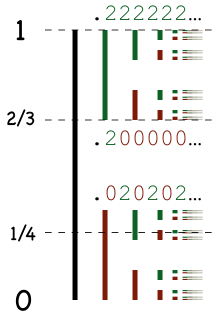
La figura muestra las siete primeras etapas:

Conjunto de Cantor.png


El conjunto de Cantor es el conjunto de los puntos restantes: entre ellos, es claro que los extremos de cada subintervalo pertenecen 0 y 1, 1/3 y 2/3, 1/9, 2/9, 7/9 y 8/9, 1/27..., hay una infinidad de puntos: los 1/3n están todos incluidos, con n describiendo los naturales. Pero hay mucho más, por ejemplo 1/4 es un elemento del conjunto de Cantor.

Propiedades

Medida

Sin embargo, el conjunto es pequeño cuando se considera su longitud: el intervalo inicial [0,1] mide 1, y a cada paso, se le quita un tercio, lo que hace que su longitud se multiplique por 2/3. la sucesión geométrica un = (2/3)n tiende hacia cero, Por lo tanto el conjunto de Cantor es de medida nula. Esto implica, en particular, que el conjunto de Cantor no puede contener ningún intervalo de medida no nula.

Cardinalidad

Podemos demostrar el siguiente resultado paradójico: el conjunto de Cantor está en biyección con el segmento [0, 1], es decir, tiene tantos elementos como él.

Para demostrar eso, vamos a construir una función suprayectiva desde el conjunto de Cantor (llamémosle C) al conjunto de los reales [0, 1]. De esta forma, la cardinalidad de C ha de ser no menor que la de [0, 1]. Por otra parte, como C es un subconjunto de [0, 1], C además ha de tener una cardinalidad no mayor. Por tanto se concluye que las cardinalidades de C y [0, 1] han de ser iguales.

La función suprayectiva la construiremos así: Si se considera la escritura en base tres de los números, se nota que, al quitar siempre el segundo tercio de todos los segmentos, se suprime exactamente los números que tienen un 1 en su escritura trienal: el intervalo (1/3; 2/3) corresponde a los números que empiezan por 0,1 (menos el 1/3 que también se puede escribir 0, 02222222222..... en base tres); el intervalo (1/9;2/9) corresponde a los números que empiezan por 0,01, el (7/9;8/9) por 0,21 y así sucesivamente.

La suprayección se construye así: a cada número escrito con sólo ceros y dos se le hace corresponder el número en base dos obtenido remplazando todos sus dos por unos. Por ejemplo, 0,2002 en base tres (que vale 2/3 + 2/81 = 56/81) tiene como imagen 0,1001 en base dos (que vale 1/2 + 1/16 = 9/16).
Se obtiene así todos los números en base dos que empiezan por 0,... y que tienen ceros o/y unos después de la coma: ¡es el intervalo [0,1] entero!

Propiedades topológicas

El conjunto de Cantor es cerrado en los reales, al ser el complemento de la unión de abiertos.[3] Al ser también acotado, por aplicación del teorema de Heine-Borel, puede afirmarse que es compacto. Se demuestra que es un conjunto denso en ninguna parte.

Autosimilaridad

El conjunto de Cantor puede considerarse también como el atractor asociado al IFS (sistema de funciones iteradas) formado por las aplicaciones contractivas f_1(x)= \frac{x}{3} , y f_2(x)= \frac{x}{3} + \frac{2}{3} , ambas definidas sobre el compacto [0,1].[4]

Observamos que la imagen del conjunto de Cantor por la homotecia de centro 0 y razón 1/3 es una parte del propio conjunto de Cantor. Esto es una manifestación de autosimilaridad, que es una de las propiedades básicas de los fractales. Su dimensión de Hausdorff es menor que uno, concretamente Log(2)/Log(3).

Generalizaciones

En dimensión uno

En lugar de eliminar en cada paso la tercera parte central, podríamos plantearnos eliminar cualquier otro porcentaje fijo (distinto de 0% o de 100%) de la zona central. Los conjuntos resultantes siguen siendo homeomorfos al conjunto de Cantor. Sin embargo, mientras la longitud del intervalo eliminado sea mayor o igual a la tercera parte, la medida de Lebesgue del conjunto será cero; en otro caso, la medida será positiva (más específico, la medida de Lebesgue es de 1-a, donde a es la razón de longitudes entre el intervalo eliminado en el primer paso y 1/3).

Eliminando porcentajes que disminuyan progresivamente en cada paso, podemos construir conjuntos también homeomorfos al conjunto de Cantor, pero con medida de Lebesgue positiva. Un ejemplo de dicha construcción es el conjunto de Smith-Volterra-Cantor.

En otras dimensiones

En cualquier dimensión se define el producto cartesiano del conjunto de Cantor por sí mismo, que recibe el nombre de polvo de Cantor. Además, en dimensión 2 se define la alfombra de Sierpinski, y en dimensión 3 la esponja de Menger.

Polvo de Cantor en 3 D.
Alfombra de Sierpinski.
Esponja de Menger.

Referencias

  1. ↑ Georg Cantor, On the Power of Perfect Sets of Points (De la puissance des ensembles parfait de points), Acta Mathematica 4 (1884) 381--392. English translation reprinted in Classics on Fractals, ed. Gerald A. Edgar, Addison-Wesley (1993) ISBN 0-201-58701-7
  2. ↑ GRIBBIN, John. Asi de Simple. El caos, la complejidad y la aparición de la vida. MAdrid, Critica. ISBN: 84-8432-716-7
  3. ↑ L. A. Steen, J. A. Seebach. Counterexamples in topology. Courier Dover Publications, 1995. ISBN 0-486-68735-X
  4. ↑ M. Barnsley. Fractals everywhere.Academic Press Inc, 1988. ISBN 0-12-079062-9.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Conjunto de Cantor — El conjunto de Cantor es, además de una curiosidad matemática, una paradoja, en el sentido usual, es decir que contradice una intuición universal relativa a tamaño de objetos geométricos. Se construye así: ● El primer paso es tomar el intervalo… …   Enciclopedia Universal

  • Conjunto de Smith-Volterra-Cantor — Después de eliminarse los intervalos negros, los puntos blancos que quedan forman un conjunto que no es denso en ninguna parte, de medida 1/2. En matemáticas, el conjunto de Smith Volterra Cantor (SVC) o el conjunto gordo de Cantor (en inglés fat …   Wikipedia Español

  • Conjunto no numerable — Un conjunto no numerable es un conjunto que no puede ser enumerado, es decir, un conjunto tal que no existe una función sobreyectiva del conjunto de los número naturales a dicho conjunto. Es decir, un conjunto A es no numerable si no existe… …   Wikipedia Español

  • Conjunto numerable — En matemáticas, un conjunto es numerable o contable cuando sus elementos pueden ponerse en correspondencia uno a uno con el conjunto de los números naturales o un subconjunto finito del mismo. Algunos autores toman una definición alternativa de… …   Wikipedia Español

  • Conjunto — Los diversos polígonos en la imagen constituyen un conjunto. Algunos de los elementos del conjunto, además de ser polígonos son regulares. La colección de estos últimos los polígonos regulares en la imagen es otro conjunto, en particular, un… …   Wikipedia Español

  • Conjunto potencia — En matemáticas, dado un conjunto S, se llama conjunto potencia o conjunto de partes de S (se denota por P(S) o 2S) al conjunto formado por todos los subconjuntos posibles de S. En la teoría de conjuntos basada en los Axiomas de Zermelo Fraenkel,… …   Wikipedia Español

  • Conjunto singular — Se llama conjunto singular en la teoría de conjuntos a todo conjunto que se contiene a sí mismo. Este tipo de conjuntos es la base de ciertas paradojas matemáticas que, como la paradoja de Russell o la paradoja del conjunto de todos los conjuntos …   Wikipedia Español

  • Cantor, Georg — (3 mar. 1845, San Petersburgo, Rusia–6 ene. 1918, Halle, Alemania). Matemático alemán, fundador de la teoría de conjuntos. Fue el primero en examinar sistemas de números, como los números racionales y los números reales, sistemáticamente como… …   Enciclopedia Universal

  • Función de Cantor — En matemáticas, la función de Cantor, llamada así en honor de Georg Cantor, es un ejemplo de función matemática que es continua pero no absolutamente continua. También se la conoce como la escalera del Diablo. La función de Cantor guarda una… …   Wikipedia Español

  • Georg Cantor — Nacimiento 3 de marzo de 1845 San Petersburgo, Rusia Fallecimiento …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”