- Tensor tensión
-
Componentes del tensor tensión en un punto P de un sólido deformable.
En mecánica de medios continuos, el tensor tensión o tensor de tensiones es el tensor que da cuenta de la distribución de tensiones y esfuerzos internos en el medio continuo.
Contenido
Tipos de tensor tensión
Tensor tensión de Cauchy
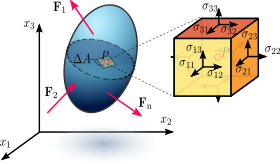
Representación gráfica de las componentes del tensor tensión en una base ortogonal.El teorema de Cauchy sobre las tensiones de un cuerpo, establece que dada una distribución de tensiones internas sobre la geometría de un medio continuo deformado, que satisfaga las condiciones del principio de Cauchy existe un campo tensorial T simétrico definido sobre la geometría deformada con las siguientes propiedades:
- .
,](1/7c13c5ad8df1f2d5a3910498f7b31640.png)
- .
- .
La tercera propiedad significa que este tensor vendrá dado sobre las coordenadas especificadas por una matriz simétrica. Cabe señalar que en un problema mecánico a priori es difícil conocer el tensor tensión de Cauchy ya que este está definido sobre la geometría del cuerpo una vez deformado, y ésta no es conocida de antemano. Por tanto previamente es necesario encontrar la forma deformada para conocer exactamente el tensor de Cauchy. Sin embargo, cuando las deformaciones son pequeñas, en ingeniería y aplicaciones prácticas se emplea este tensor aunque definido sobre las coordenadas del cuerpo sin deformar (lo cual no conduce a errores de cálculo excesivo si todas las deformaciones máximas son inferiores a 0,01).
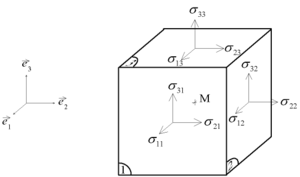
Fijado un sistema de referencia ortogonal, el tensor tensión de Cauchy viene dado por una matriz simétrica, cuyas componentes son:
La segunda forma es la forma común de llamar a las componentes del tensor tensión en ingeniería.Primer tensor tensión de Piola-Kirchhoff
Los tensores de Piola-Kirchhoff TR se introducen para evitar la dificultad de tener que trabajar con un tensor definido sobre la geometría ya deformada (que normalmente no es conocida de antemano). La relación entre ambos tensores viene dada por:
Donde F es el tensor gradiente de deformación. Este tensor sin embargo, tiene el problema de que no es simétrico (ver segundo tensor tensión de Piola-Kirchhoff).
Segundo tensor tensión de Piola-Kirchhoff
Este tensor se introduce para lograr un tensor definido sobre la geometría previa a la deformación y que además sea simétrico, a diferencia del primer tensor de Piola-Kirchhoff que no tiene por qué ser simétrico. El segundo tensor tensión de Piola-Kirchhoff viene dado por:
Véase también
- Mecánica de medios continuos
- Elasticidad (mecánica de sólidos)
- Teorema de Rivlin-Ericksen
- Tensor deformación
Referencias
Bibliografía
- R. J. Atkin & N. Fox: An Introduction to the Theory of Elasticity, ed. Dover, ISBN 0-486-44241-1, 1980.
Categorías:- Mecánica de medios continuos
- Magnitudes físicas
- Ingeniería estructural
- .
![[T_C]_{xyz} =
\begin{bmatrix}
\sigma_{11} & \sigma_{12} & \sigma_{13} \\
\sigma_{21} & \sigma_{22} & \sigma_{23} \\
\sigma_{31} & \sigma_{32} & \sigma_{33}
\end{bmatrix} =
\begin{bmatrix}
\sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\
\sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\
\sigma_{zx} & \sigma_{zy} & \sigma_{zz}
\end{bmatrix} =
\begin{bmatrix}
\sigma_x & \tau_{xy} & \tau_{xz} \\
\tau_{yx} & \sigma_y & \tau_{yz} \\
\tau_{zx} & \tau_{zy} & \sigma_z
\end{bmatrix}](9/939382eca7a41bd5944da1e16f21626e.png)
Wikimedia foundation. 2010.
