Tensor de energía-impulso

Tensor de energía-impulso
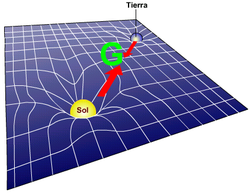En relatividad general la curvatura del espacio-tiempo vienen dada por el tensor de energía-impulso.

El tensor de tensión-energía, también llamado tensor energía-impulso (o igualmente tensor de energía - momento) es una cantidad tensorial en la teoría de la relatividad que se usa para describir el flujo de energía y el momento lineal de una distribución continua de materia en el contexto de la teoría de la relatividad, ademàs de ser de suma importancia en las ecuaciones de Einstein para el campo gravitacional.

Contenido

Introducción

Fijado un conjunto de coordenadas o una base \scriptstyle \{ {\mathbf{e}}^0, {\mathbf{e}}^1, {\mathbf{e}}^2, {\mathbf{e}}^3 \} en cada punto del espacio-tiempo (los elementos de esta base sería matemáticamente 1-formas), el tensor energía-impulso es un tensor de rango 2 que puede describirse como una matriz del tipo:

\mathbf{T}(\mathbf{x}) = T_{\alpha\beta}(\mathbf{x}) {\mathbf{e}}^\alpha {\mathbf{e}}^\beta, \qquad T_{\alpha\beta} = \begin{bmatrix} T_{00} & T_{01} & T_{02} & T_{03} \\ T_{10} & T_{11} & T_{12} & T_{13} \\ T_{20} & T_{21} & T_{22} & T_{23} \\ T_{30} & T_{31} & T_{32} & T_{33} \end{bmatrix}

Donde en la expresión anterior se ha usado el convenio de sumación de Einstein. Si consideramos ahora un observador que se mueve con cuadrivelocidad \scriptstyle \mathbf{u} = u^\alpha\mathbf{e}_\alpha tenemos que la densidad de energía medida en un punto \scriptstyle \mathbf{x} por dicho observador viene dada por:

e = T_{\alpha\beta}(\mathbf{x})\frac{u^\alpha u^\beta}{c^2}

Y el flujo de energía a través de una superficie (de tipo espacial y en reposo respecto al observador) cuyo vector normal venga dado por \scriptstyle \mathbf{n} viene dado por:

-T_{\alpha\beta}(\mathbf{x}) u^\alpha n^\beta

Ley de conservación

En el contexto de la teoría de la relatividad, la ley de conservación de la energía y la ley de conservación de la cantidad de movimiento pueden expresarse de manera muy simple en términos del tensor de energía-impulso. Concretamente ambas leyes pueden escribirse conjuntamente como una ecuación de continuidad del tipo:

\nabla_\mu T^{\mu\nu}=0

La cantidad

P^\mu = \frac{1}{c} \int_V T^{0\mu}\ d^3 \mathbf{x}

sobre una rebanada de tipo espacio da el cuadrivector energía-momento o cuadrimomento. Este tensor es la corriente de Noether asociada a las translaciones en el espacio-tiempo. En relatividad general, esta cantidad actúa como la fuente de la curvatura del espacio-tiempo, y es la densidad de corriente asociada a las transformaciones de gauge (en este caso transformaciones de coordenadas) por el teorema de Noether. Ahora bien, en el espacio-tiempo curvado,la integral de tipo espacio depende de la rebanada de tipo espacio, en general. No hay de hecho manera de definir un vector global de energía-momento en un espacio-tiempo curvado en general.

Tensores relacionados

La parte tridimensional del tensor energía-impulso coincide con el tensor tensión de la mecánica de medios continuos.

Ejemplos

  • En teoría de la relatividad el tensor energía-impulso de un fluido perfecto es expresable en términos de su cuadrivelocidad, densidad másica y presión:

(1) T_{\mu\nu}= \left(\rho + \frac{p}{c^2}\right) u_\mu u_\nu + p g_{\mu\nu}

Véase también

Referencias

Bibliografía

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Tensor métrico — En geometría de Riemann, el tensor métrico es un tensor de rango 2 que se utiliza para definir conceptos métricos como distancia, ángulo y volumen en un espacio localmente euclídeo. Contenido 1 Definición 2 Longitud, ángulo y volumen 3 …   Wikipedia Español

  • Energía — Para otros usos de este término, véase Energía (desambiguación). Un rayo es una forma de transmisión de energía. El término energía (del griego ἐνέργεια/energeia, actividad, operación; ἐνεργóς/energos = fuerza de acción o fuerza trab …   Wikipedia Español

  • Conservación de la energía — Sistema mecánico en el cual se conserva la energía, para choque perfectamente elástico y ausencia de rozamiento. La ley de la conservación de la energía constituye el primer principio de la termodinámica y afirma que la cantidad total de energía… …   Wikipedia Español

  • Energía cinética — Saltar a navegación, búsqueda Para otros usos de este término, véase Cinética. Los carros de una montaña rusa alcanzan su máxima energía cinética cuando están en el fondo de su trayectoria. Cuando comienzan a elevarse, la energía cinética comienz …   Wikipedia Español

  • Relatividad general — Algunas partes de este artículo pueden resultar complicadas, en ese caso se recomienda Introducción a la relatividad general Representación artística de la explosión de la supernova SN 2006gy, situada a 238 millones de años luz. De ser válido el… …   Wikipedia Español

  • Teoría de la Relatividad — Saltar a navegación, búsqueda Con el nombre de Teoría de la Relatividad se engloban generalmente dos cuerpos de investigación en ciencias físicas, usualmente conectadas con las investigaciones del físico Albert Einstein: su Teoría de la… …   Wikipedia Español

  • Teoría de la relatividad — Dibujo artístico sobre la teoría de la relatividad La teoría de la relatividad incluye dos teorías (la de la relatividad especial y la de la relatividad general) formuladas por Albert Einstein a principios del siglo XX, que pretendían resolver la …   Wikipedia Español

  • Espacio-tiempo — Saltar a navegación, búsqueda Analogía bidimensional de la distorsión del espacio tiempo debido a una gran masa. El espacio tiempo es la entidad geométrica en la cual se desarrollan todos los eventos físicos del Universo, de acuerdo con la teoría …   Wikipedia Español

  • Glosario de relatividad — Anexo:Glosario de relatividad Saltar a navegación, búsqueda Este artículo contiene un glosario términos comúnmente usados en teoría de la relatividad. Se definen algunos de los términos brevemente y se enlaza a un artículo más amplio si éste… …   Wikipedia Español

  • Anexo:Glosario de relatividad — Este artículo contiene un glosario términos comúnmente usados en teoría de la relatividad. Se definen algunos de los términos brevemente y se enlaza a un artículo más amplio si éste existe. Índice: A B C D E F G H I J K L M N Ñ O P Q R S T U V W… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”