Teorema de Gauss-Bonnet

Teorema de Gauss-Bonnet
Un ejemplo de región compleja donde el teorema de Gauss-Bonnet puede ser aplicado. Se muestra el signo de la curvatura geodésica.

El teorema de Gauss-Bonnet en geometría diferencial es una proposición importante sobre superficies que conecta su geometría (en el sentido de la curvatura) con su topología (en el sentido de la característica de Euler).

Contenido

Definición

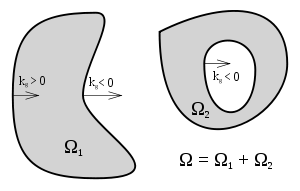
Supóngase que M es una variedad de Riemann compacto orientable de dimensión 2, con borde \partial M. Denótese por K la curvatura gaussiana en los puntos de M y por kg la curvatura geodésica en los puntos de \partial M. Entonces

\int_M K\;dA-\int_{\partial M}k_g\;ds=2\pi\chi(M)

donde χ(M) es la característica de Euler de M.

El teorema se puede aplicar en particular si la variedad no tiene borde, en cuyo caso la integral \int_{\partial M}k_g\;ds puede ser omitido.

Si se dobla o deforma la variedad M su característica de Euler no cambiará, mientras que las curvaturas en los puntos dados sí. El teorema requiere, algo asombrosamente, que la integral total de todas las curvaturas siga siendo igual.

Generalizacines

Una generalización a n dimensiones fue encontrada en los años 40 por Allendoerfer, Weil y Chern. Ver el teorema de Gauss-Bonnet generalizado y el homomorfismo de Chern-Weil.

Véase también

Enlaces externos

Weisstein, Eric W. «Gauss-Bonnet Formula» (en inglés). MathWorld. Wolfram Research.


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Teorema de Gauss-Bonnet — El teorema de Gauss Bonnet en geometría diferencial es una proposición importante sobre superficies que conecta su geometría (en el sentido de la curvatura) con su topología (en el sentido de la característica de Euler). Supóngase que M es una… …   Enciclopedia Universal

  • Teorema de Gauss-Bonnet generalizado — En matemáticas, el teorema de Gauss Bonnet generalizado presenta la característica de Euler de una variedad de Riemann cerrada como integral de cierto polinomio derivado de su curvatura. Es una generalización directa del teorema de Gauss Bonnet a …   Wikipedia Español

  • Teorema de Gauss-Bonnet generalizado — En matemáticas, el teorema de Gauss Bonnet generalizado presenta la característica de Euler de una variedad de Riemann cerrada como integral de cierto polinomio derivado de su curvatura. Es una generalización directa del teorema de Gauss Bonnet a …   Enciclopedia Universal

  • Gauss — Saltar a navegación, búsqueda Gauss se puede referir a: El matemático y físico Carl Friedrich Gauss; La unidad de medida de campo magnético gauss. Términos relacionados: La distribución de Gauss o distribución normal es una distribución de… …   Wikipedia Español

  • Gauss (desambiguación) — Carl Friedrich Gauss fue un matemático y físico alemán. Gauss también puede referirse a: La unidad de medida de campo magnético gauss. Véase también La distribución de Gauss o distribución normal es una distribución de probabilidad muy… …   Wikipedia Español

  • Característica de Euler — Saltar a navegación, búsqueda En topología algebraica, la característica de Euler o característica de Euler Poincaré es un invariante topológico (de hecho, invariante homotópico) definido para una amplia clase de espacios topológicos. Es denotada …   Wikipedia Español

  • Shiing-Shen Chern — 220px Nacimiento 26 de octubre de 1911 Jiaxing, Zhejiang,China Fallecimiento 3 de diciembre de 2004 Tianjin,China …   Wikipedia Español

  • Geometría riemanniana — Saltar a navegación, búsqueda En geometría diferencial, la geometría riemanniana es el estudio de las variedades diferenciales con métricas de Riemann; es decir de una aplicación que a cada punto de la variedad, le asigna una forma cuadrática… …   Wikipedia Español

  • Geometría de Riemann — En geometría diferencial, la geometría de Riemann es el estudio de las variedades diferenciales con métricas de Riemann; es decir de una aplicación que a cada punto de la variedad, le asigna una forma cuadrática definida positiva en su espacio… …   Wikipedia Español

  • Clase característica — En matemáticas, una clase característica es un elemento del módulo de cohomología de un espacio topológico y que satisfacen ciertos axiomas considerando varias de ellas. Son un concepto unificador entre la topología algebraica, geometría… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”