Teorema de la divergencia

Teorema de la divergencia

En cálculo vectorial, el teorema de la divergencia, también llamado teorema de Gauss o teorema de Gauss-Ostrogradsky, teorema que relaciona el flujo de un campo vectorial a través de una superficie cerrada con la integral de su divergencia en el volumen delimitado por dicha superficie. Intuitivamente se puede concebir como la suma de todas las fuentes menos la suma de todos los sumideros da el flujo de salida neto de una región. Es un resultado importante en física, sobre todo en electrostática y en dinámica de fluidos. Desde el punto de vista matemático es un caso particular del teorema de Stokes.

Contenido

Historia

El teorema fue descubierto originariamente por Joseph Louis Lagrange en 1762, e independientemente por Carl Friedrich Gauss en 1813, por George Green en 1825 y en 1831 por Mikhail Vasilievich Ostrogradsky, que también dio la primera demostracion del teorema. Posteriormente, variaciones del teorema de divergencia se conocen como teorema de Gauss, el teorema de Green, y teorema de Ostrogradsky.

Enunciado

Sean H\, y U\,dos subconjuntos abiertos en \mathbb{R}^3 donde U\subset H es simplemente conexo y el borde de U\,, S\, es una superficie regular o regular a trozos y cerrada.

Sea \mathbf F : H\to \mathbb{R}^3, un campo vectorial de clase C^1\,, es decir, \mathbf {F} cuenta con derivadas parciales de primer orden continuas.

Entonces:

No se pudo entender (La conversión a PNG ha sido errónea): \iint\limits_{S} \mathbf F \cdot \hat\mathbf n \ dS = \iiint\limits_{U} \boldsymbol\nabla\cdot\mathbf F \;dV

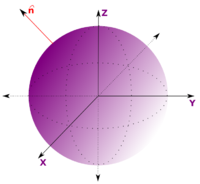
donde el vector No se pudo entender (La conversión a PNG ha sido errónea): \hat\mathbf n\,

normal a la superficie apunta hacia el exterior del volumen V\,.

Este resultado es una consecuencia natural del Teorema de Stokes, el cual generaliza el Teorema fundamental del cálculo. El teorema fue enunciado por el matemático alemán Carl Friedrich Gauss en 1835, pero no fue publicado hasta 1867. Debido a la similitud matemática que tiene el campo eléctrico con otras leyes físicas, el teorema de Gauss puede utilizarse en diferentes problemas de física gobernados por leyes inversamente proporcionales al cuadrado de la distancia, como la gravitación o la intensidad de la radiación. Este teorema recibe el nombre de ley de Gauss y constituye también la primera de las ecuaciones de Maxwell.

Ejemplo de aplicación

Esfera de radio 2.

Calcular el flujo del campo vectorial \mathbf F(x,y,z)=x\mathbf i+y\mathbf j+z\mathbf k a través de la superficie esférica x^{\,\!2} + y^{\,\!2} + z^{\,\!2} = 4

Resolución. A partir de la ecuación de la esfera se sabe que el radio es R \,=2. Entonces:

\boldsymbol\nabla\cdot\mathbf F = \frac{\partial f_1 \;}{\partial x \;} + \frac{\partial f_2 \;}{\partial y \;} + \frac{\partial f_3 \;}{\partial z \;}= 1 + 1 + 1 = 3

Aplicando el teorema de la divergencia tenemos:

\iint_{S} \mathbf F \cdot \mathbf n \ dS = \iiint_{V} \boldsymbol\nabla\cdot\mathbf F \ dV = \iiint_{V} 3\,\ dV = 3\,\iiint_{V} \ dV = 3V = 3 \times \frac{4}{3} \pi \times 2^3 = 32\, \pi

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Teorema de la divergencia — En cálculo vectorial, el teorema de la divergencia, también llamado teorema de Gauss o teorema de Gauss Ostrogradsky es un teorema que relaciona la divergencia de un campo vectorial con el valor de la integral de superficie del flujo definido por …   Enciclopedia Universal

  • Divergencia (matemática) — Saltar a navegación, búsqueda La divergencia de un campo vectorial mide la diferencia entre el flujo entrante y el flujo saliente de un campo vectorial sobre la superficie que rodea a un volumen de control, por tanto, si el campo tiene fuentes o… …   Wikipedia Español

  • Gauss, teorema de o teorema de la divergencia — ► MATEMÁTICAS Teorema elaborado por K. F. Gauss en el que establece que dado un campo vectorial y un volumen V limitado por una superficie S, se cumple , donde div simboliza el operador divergencia …   Enciclopedia Universal

  • Teorema de Stokes — El teorema de Stokes en geometría diferencial es una proposición sobre la integración de formas diferenciales que generaliza varios teoremas del cálculo vectorial. Se nombra así por George Gabriel Stokes (1819 1903), a pesar de que la primera… …   Wikipedia Español

  • Divergencia — ► sustantivo femenino 1 Movimiento por el que dos cosas se van apartando o separando progresivamente. ANTÓNIMO convergencia 2 Discrepancia, diversidad de opiniones: ■ sus divergencias crearon tensión en el gabinete. SINÓNIMO desacuerdo * * *… …   Enciclopedia Universal

  • Teorema de equipartición — Figura 1. Movimiento térmico de un péptido tipo hélice α. El movimiento vibratorio es aleatorio y complejo, y la energía de un átomo en particular puede fluctuar ampliamente. Sin embargo, el teorema de equipartición permite que se pueda calcular… …   Wikipedia Español

  • Teorema de Green — En física y matemáticas, el teorema de Green da la relación entre una integral de línea alrededor de una curva cerrada simple C y una integral doble sobre la región plana D limitada por C. El teorema de Green se llama así por el científico… …   Wikipedia Español

  • Teorema de Mermin-Wagner — En Teoría cuántica de campos y mecánica estadística, el teorema de Mermin Wagner establece que las simetrías continuas no pueden ser rotas instantáneamente a temperatura finita en sistemas con interacciones de corto alcance en dimensiones . Esto… …   Wikipedia Español

  • Teorema de Earnshaw — El texto que sigue es una traducción defectuosa o incompleta. Si quieres colaborar con Wikipedia, busca el artículo original y mejora o finaliza esta traducción. Puedes dar aviso al autor principal del artículo pegando el siguiente código en su… …   Wikipedia Español

  • Teorema de la telaraña — El teorema de la telaraña explica el modelo general que sigue la formación de los precios de los productos cuya oferta se establece en función del precio de mercado observado en el período inmediatamente anterior (sea este un día, semana,… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”