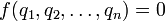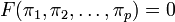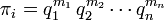Teorema de Pi-Buckingham

Teorema de Pi-Buckingham

Teorema de Pi-Buckingham

El Teorema de Pi de Vaschy-Buckingham es el teorema fundamental del análisis dimensional. El teorema establece que dada una ecuación física en la que están involucradas n variables físicas, si dichas variables se expresan en términos de k cantidades físicas independientes, entonces la ecuación original es equivalente a una ecuación con una serie de p = n - k números adimensionales construidos con las variables originales.

Este teorema proporciona un método de construcción de parámetros adimensionales incluso cuando la forma de la ecuación es desconocida. De todas formas la elección de parámetros adimensionales no es única y el teorema no elige cuáles tienen significado físico.

Exposición

Más formalmente, el número de términos adimensionales construidos p es igual a la nulidad de la matriz dimensional en donde k es el rango de la matriz.

En términos matemáticos, si tenemos una ecuación física tal que:

f(q_1,q_2,\ldots,q_n)=0\,\!

en donde qi  son las n  variables físicas, y se expresan en términos de k  unidades físicas independientes. Entonces la anterior ecuación se puede reescribir como:

F(\pi_1,\pi_2,\ldots,\pi_p)=0\,\!

en donde πi son los parámetros adimensionales construidos de p = n − k  ecuaciones de la forma:

\pi_i=q_1^{m_1}\,q_2^{m_2}\cdots q_n^{m_n}

en donde los exponentes mi  son números racionales.

La utilización de πi como parámetros adimensionales fue introducida por Edgar Buckingham en su artículo de 1.914, de ahí el nombre del teorema.

Enlaces externos

Generalización del teorema Pi de Buckingham [1]

Obtenido de "Teorema de Pi-Buckingham"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Teorema de Vaschy-Buckingham — Saltar a navegación, búsqueda Teorema de Vaschy Buckingham Para reducir un problema dimensional a otro adimensional con menos parámetros, se siguen los siguientes pasos generales: Contar el número de variables dimensionales n. Contar el número de …   Wikipedia Español

  • Teorema π de Vaschy-Buckingham — El Teorema de Π (pi) de Vaschy Buckingham es el teorema fundamental del análisis dimensional. El teorema establece que dada una relación física expresable mediante una ecuación en la que están involucradas n magnitudes físicas o variables, y si… …   Wikipedia Español

  • Análisis dimensional — Saltar a navegación, búsqueda El análisis dimensional es una poderosa herramienta que permite simplificar el estudio de cualquier fenómeno en el que estén involucradas muchas magnitudes físicas en forma de variables independientes. Su resultado… …   Wikipedia Español

  • Número adimensional — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Turbomáquina — Ventilador de escritorio Westinghouse antiguo, fácilmente se puede identificar que es una turbomáquina, obsérvese que intercambia energía con el aire que impulsa y que su parte principal es una rueda con palas …   Wikipedia Español

  • Intercambiador de calor dinámico de superficie rascada — Un intercambiador de calor dinámico de superficie rascada es un dispositivo diseñado para intercambiar la máxima cantidad de calor por unidad de área mediante la generación de tanta turbulencia como sea posible. Contenido 1 Introducción 2… …   Wikipedia Español

  • Wilhelm Nusselt — Ernst Kraft Wilhelm Nußelt o más usualmente Wilhelm Nusselt (Nuremberg, 25 de noviembre de 1882 Munich, 1 de septiembre de 1957) fue un ingeniero alemán. Estudió ingeniería mecánica en la Universidad Técnica de Munich (Technische Universität… …   Wikipedia Español

  • Homosexualität im Film — Diese Liste enthält Filme mit homosexuellem Inhalt, sei es eine dargestellte Einzelperson in mehr als einer Nebenrolle oder eine gleichgeschlechtliche Begegnung. Chronologische Filmliste 1910er Jahre Anders als die Andern (D 1919) Regie: Richard… …   Deutsch Wikipedia

  • Liste von Filmen mit homosexuellem Inhalt — Diese Liste enthält Filme mit homosexuellem Inhalt, sei es eine dargestellte Einzelperson in mehr als einer Nebenrolle oder eine gleichgeschlechtliche Begegnung. Chronologische Filmliste 1910er | 1920er | 1930er | 1940er | 1950er | 1960er |… …   Deutsch Wikipedia

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”