Transformada de Abel

Transformada de Abel

En matemáticas, la transformada de Abel, llamada así por Niels Henrik Abel, es una transformada integral frecuentemente usada en el análisis de funciones de simetría esférica o axial. La transformada de Abel de una función f(r) está dada por:

F(y)=2\int_y^\infty \frac{f(r)r\,dr}{\sqrt{r^2-y^2}}.

Si f(r) tiende a cero más rápidamente que 1/r, la transformada inversa de Abel viene dada por

f(r)=-\frac{1}{\pi}\int_r^\infty\frac{d F}{dy}\,\frac{dy}{\sqrt{y^2-r^2}}.

En análisis de imágenes, se usa una transformada de Abel para proyectar una función de emisión ópticamente delgada y de simetría axial sobre un plano. La transformada inversa se usa para calcular la función de emisión, dada una cierta proyección (ej. un escaneo o una fotografía) de esta función.

Recientemente la transformada inversa de Abel (y sus variantes) se ha convertido en la piedra angular del análisis de datos de imágenes tipo fotón/fragmento/ion (photofragment-ion imaging) y fotón/electrón (photoelectron imaging). Entre las más notables extensiones recientes de la transformada inversa de Abel están los métodos Onion Peeling y BAsis Set Expansion (BASEX) para análisis de imágenes tipo fotón/electrón y fotón/ion.

Contenido

Interpretación geométrica

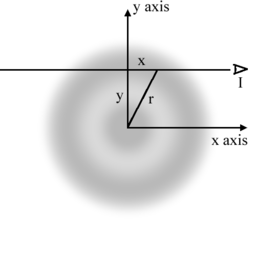Una interpretación geométrica de la transformada de Abel en dos dimensiones. Un observador (I) mira a lo largo de la línea paralela al eje x a una distancia y sobre el origen. Lo que el observador mira es la proyección (i.e. la integral) de la función de simetría circular f(r) a lo largo de la línea de visión. La función f(r) está representada en gris en ésta figura.Se asume que el observador está localizado infinitamente lejos del origen de manera que los límites de integración son ±∞.

En dos dimensiones, la transformada de Abel F(y) puede ser interpretada como la función de simetría circular f(r) a lo largo de un conjunto de líneas de visión, las cuales están a una distancia y desde el origen. En referencia a la figura de la derecha, el observador (I) verá:

F(y)=\int_{-\infty}^\infty f(\sqrt{x^2 + y^2})\,dx

donde f(r) es la función de simetría circular representada en gris en la figura. Se asume que el observador está en x = ∞ de manera que los límites de integración son ±∞ y todas las líneas de visión son paralelas al eje x. Notando que el radio r se relaciona con x y con y via r2 = x2 + y2, se sigue que:

dx=\frac{r\,dr}{\sqrt{r^2-y^2}}.

El intervalo de integración en r no pasa por cero, y ya que ambos f(r) y la expresión de arriba para dx son funciones pares, podemos escribir:

\int_{-\infty}^\infty f(r)dx=2\int_0^\infty f(r)\,dx, \;\; r= \sqrt{x^2+y^2}.

Substituyendo la expresión paradx en términos de ry reescribiendo los límites de integración acordemente, resulta la transfomada de Abel.

La transformada de Abel puede extenderse a dimensiones más altas. La extensión a tres dimensiones es de particular interés. Si tenemos una función de simetría axial f(ρ,z) donde ρ2 = x2 + y2 es el radio cilíndrico, entonces podríamos querer saber la proyección de esa función sobre el plano paralelo al eje z. Sin pérdida de generalidad, podemos escoger el plano yz de manera que:

F(y,z) =\int_{-\infty}^\infty f(\rho,z)\,dx =2\int_y^\infty \frac{f(\rho,z)\rho\,d\rho}{\sqrt{\rho^2-y^2}}

la cual es justo la transformada de Abel de f(ρ,z) en ρ y y.

La simetría esférica es un tipo particular de simetría axial. En éste caso, tenemos la función f(r) donde r2 = x2 + y2 + z2. La proyección sobre, digamos el plano yz, será circularmente simétrica y expresable como F(s) donde s2 = y2 + z2. Efectuando la integración, tenemos:

F(s) =\int_{-\infty}^\infty f(r)\,dx =2\int_s^\infty \frac{f(r)r\,dr}{\sqrt{r^2-s^2}}

lo cual es también la transformada de Abel de f(r) en r y s.

Verificación de la transformada inversa de Abel

Asumiendo que f es continua y diferenciable en todo punto y que f, f' tienden a cero más rápido que 1/r, podemos hacer u = f(r) y v=\sqrt{r^2-y^2} . Integrando por partes se tendrá:

F(y) = -2 \int_y^\infty f'(r) \sqrt{r^2-y^2} \, dr.

Diferenciando formalmente,

F'(y) = 2 y \int_y^\infty \frac{f'(r)}{\sqrt{r^2-y^2}} \, dr.

Ahora, substituyendo esto en la fórmula de la transformada inversa de Abel:

-\frac{1}{\pi} \int_r^\infty \frac{F'(y)}{\sqrt{y^2-r^2}} \, dy = \int_r^\infty \int_y^\infty \frac{-2 y}{\pi \sqrt{(y^2-r^2) (s^2-y^2)}} f'(s) \, ds dy.

Por el Teorema de Fubini, la última integral es igual a:

\int_r^\infty \int_r^s \frac{-2 y}{\pi \sqrt{(y^2-r^2) (s^2-y^2)}} \, dy f'(s) \,ds = \int_r^\infty (-1) f'(s) \, ds = f(r).

Relación con otras transformadas integrales

Relación con las transformadas de Fourier y Hankel

La transformada de Abel es un miembro del ciclo FHA de operadores integrales. Por ejemplo, en dos dimensiones, si definimos A como el operador transformada de Abel, F como el operador transformada de Fourier y H como el operador transformada de Hankel de orden cero, entonces, un caso especial del Teorema de proyección-rebanada para funciones de simetría circular establece que:

FA=H.\,

En otras palabras, aplicando la transformada de Abel a una función 1-dimensional y luego aplicando la transformada de Fourier resulta ser lo mismo que aplicar la transformada de Hankel a esa función. Este concepto puede extenderse a más dimensiones.

Relación con la transformada de Radon

La tranformada de Abel es una proyección de f(r) a lo largo de un eje particular. La transformada de Radon 2-dimensional nos da la transformada de Abel no sólo como función de la distancia a lo largo del eje de visión, sino también como función del ángulo de éste eje.

Referencias

  • Bracewell, R. (1965). The Fourier Transform and its Applications. New York: McGraw-Hill. ISBN 0-07-007016-4. 

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Transformada integral — Para otros usos de este término, véase Transformada (desambiguación). Una transformada integral es cualquier transformada T aplicada sobre la función f(x) de la forma siguiente: La entrada de esta función T encontramos una función f(t), y la… …   Wikipedia Español

  • Abel Paulino Miguel — Abel Miguel Diputado de la Provincia de Buenos Aires por Cuarta Sección Electoral Actualmente en el cargo Desde el 10 de diciembre de 2007 …   Wikipedia Español

  • 1 − 2 + 3 − 4 + · · · — Los primeros miles de términos y sumas parciales de 1 − 2 + 3 − 4 + · · ·. En matemáticas, la expresión 1 − 2 + 3 − 4 + · · · es una serie infin …   Wikipedia Español

  • Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención …   Wikipedia Español

  • Función polilogarítmica — El polilogaritmo (también conocido como función de Jonquière) es una función especial definida por la siguiente serie: Esta no es, en general, una función elemental, aunque esté relacionada con la función logarítmica. La definición dada arriba es …   Wikipedia Español

  • Anexo:Funciones matemáticas — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Función eta de Dirichlet — η(s) en el plano complejo. El color en un punto s codifica el valor de η(s). Colores fuertes denotan valores cercanos a cero y el tono codifica el valor del argumento. En las matemáticas, en el área …   Wikipedia Español

  • Vigo — Para otros usos de este término, véase Vigo (desambiguación). Vigo Bandera …   Wikipedia Español

  • Función de Bessel — En matemática, las funciones de Bessel, primero definidas por el matemático Daniel Bernoulli y más tarde generalizadas por Friedrich Bessel, son soluciones canónicas y(x) de la ecuación diferencial de Bessel: (1) donde α es un …   Wikipedia Español

  • Fórmula de Perron — En matemática, y más precisamente en teoría analítica de números, la fórmula de Perron es una fórmula dada por Oskar Perron para calcular la suma de una función aritmética, mediante el uso de una transformada de Mellin inversa. Contenido 1… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”