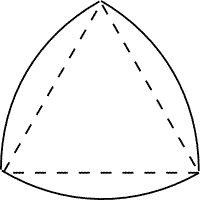El triángulo de Reuleaux es una curva de anchura constante basada en un triángulo equilátero. La distancia entre cualquier punto de una de las curvas y el vértice opuesto es la misma.

El triángulo Reuleaux es la versión más conocida de los llamados polígonos de Reuleaux, denominados así por el científico e ingeniero que los desarrolló, Franz Reuleaux. Estos polígonos tienen la particularidad de ser curvas de anchura constante, es decir, donde todos los diámetros trazados desde cualquiera de las curvas tiene la misma longitud.

El triángulo es la forma más sencilla de este tipo de polígonos, donde la distancia entre dos líneas tangentes paralelas opuestas y el borde es el mismo, independientemente de la dirección de esas líneas. Para construir un triángulo de Reuleaux hay que partir de un triángulo equilátero. Situando el compás en uno de los vértices de dicho triángulo se traza una circunferencia cuyo radio es el lado del triángulo, repitiendo lo mismo en los otros dos vértices. Borrando el triángulo inicial, el espacio central que queda entre los tres círculos es el triángulo de Reuleaux, una curva de anchura constante.

El teorema de Blaschke-Lebesgue establece que el triángulo de Reuleaux tiene menor superficie que cualquier otra curva de anchura constante dada. Esta área se define por 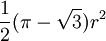, donde r es el radio constante.

El triángulo de Reuleaux puede ser generalizado a otros polígonos regulares con un número impar de lados, como puede ser el caso de las monedas británicas de 20 peniques (basadas en un heptágono).

Otros usos

• Debido a que todos sus diámetros tienen la misma longitud, el triángulo Reuleaux, junto con los demás polígonos regulares de Reuleaux, es la respuesta a la pregunta "Además de un círculo, ¿qué otra forma puede tener una tapa de alcantarilla para que no caiga a través del agujero?"
• El rotor de un Motor Wankel tiene como pieza fundamental un triángulo de Reuleaux.
• Una broca con forma de triángulo de Reuleaux puede taladrar un agujero con una forma casi exacta a la de un cuadrado perfecto.
• Un triángulo de Reuleaux puede rodar fácilmente, pero no funciona bien como rueda debido a que no tiene un centro fijo de rotación.
• La existencia de los polígonos de Reuleaux es una buena demostración de por qué no se debe usar solamente la medición del diámetro para verificar que un objeto tiene sección circular.

Versión en tres dimensiones

La intersección de esferas de radio s centradas en los vértices de tetraedros regulares con lado también s es denominado el tetraedro Reuleaux, pero en este caso no es una superficie de anchura constante. Puede, sin embargo, ser realizada dentro de una superficie de anchura constante, conocida como el tetraedro Meissner, reemplazando sus límites en forma de arco por "parches" de superficie curvada. Alternativamente, la superficie de un triángulo de Reuleaux en revolución sobre uno de sus ejes simétricos forma una superficie de anchura constante.