Geometría esférica

Geometría esférica
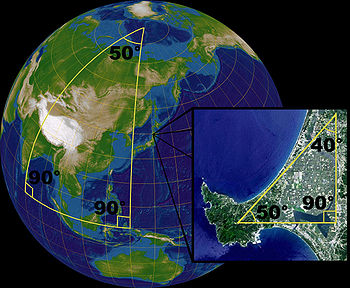En una esfera, la suma de los ángulos de un triángulo no es igual a 180°. Una esfera no es un espacio euclidiano, pero localmente las leyes de la geometría euclidiana son buenas aproximaciones. En un pequeño triángulo en la cara de la Tierra, la suma de los ángulos es muy cercana a 180°. Una esfera puede ser representada por una colección de mapas de dos dimensiones, por lo tanto una esfera es una variedad, en el triángulo curvo convexo la suma de los ángulos puede ser superior a 180°.

La geometría esférica es la geometría de la superficie bi-dimensional de una esfera. Es un ejemplo de geometría no euclídea.

En geometría plana los conceptos básicos son el punto y la línea. En la esfera, los puntos están definidos en el sentido usual. Los equivalentes de las líneas no están definidos en el sentido usual de la "línea recta" sino en el sentido de "las trayectorias más cortas entre los puntos", lo cual es llamado geodésica. En la esfera los geodésicos son los grandes círculos, así que los otros conceptos geométricos son definidos como en la geometría plana pero con las líneas sustituidas por los grandes círculos. Así, en geometría esférica los ángulos están definidos entre los grandes círculos, resultando en una trigonometría esférica que diferencie de la trigonometría ordinaria en muchos aspectos (por ejemplo, la suma de los ángulos interiores de un triángulo excede los 180 grados).

La geometría esférica es el modelo más simple de la geometría elíptica, en la cual una línea no tiene ningún línea paralela a través de un punto dado. En contraste con la geometría hiperbólica, en la cual una línea tiene dos paralelas, y un número infinito de ultra-paralelos, a través de un punto dado.

La geometría esférica tiene importantes aplicaciones prácticas en la navegación y la astronomía.

Una geometría importante relacionada con la modelada por la esfera es llamada plano proyectivo real, y es obtenida identificando las antípodas en la esfera (pares de puntos opuestos). Localmente, el plano proyectivo tiene todas las propiedades de la geometría esférica, pero tiene diferentes características globales. En particular, es no orientable.

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • geometria — s. f. 1. Ciência que tem por objeto as dimensões das linhas, das superfícies e dos volumes. 2. Tratado de geometria. 3. geometria analítica: a que emprega a análise matemática no estudo das dimensões. 4. geometria antiga: a que, em vez do cálculo …   Dicionário da Língua Portuguesa

  • Geometría del espacio — La geometría del espacio es rama de la geometría que se ocupa de las propiedades y medidas de figuras geométricas en el espacio tridimensional. Entre estas figuras, también llamadas sólidos, se encuentran el cono, el cubo, el cilindro, la… …   Enciclopedia Universal

  • Geometría elíptica — La superficie de la esfera constituye un ejemplo de geometría elíptica bidimensional. Sobre una esfera, la suma de los ángulos de un triángulo esférico no es igual a 180º. La superficie de una esfera no es un espacio euclídeo, aunque localmente… …   Wikipedia Español

  • Geometría euclidiana — La geometría euclidiana (o geometría parabólica)[1] es aquella que estudia las propiedades del plano y el espacio tridimensional. En ocasiones los matemáticos usan el término para englobar geometrías de dimensiones superiores con propiedades… …   Wikipedia Español

  • Geometría convexa — La geometría convexa es la rama de la geometría que estudia sistemas convexos, principalmente en espacio euclidiano. Los sistemas convexos ocurren naturalmente en muchas áreas de la matemática: la geometría de cómputo, el análisis convexo, la… …   Wikipedia Español

  • Geometría espacial — Se ha sugerido que este artículo o sección sea fusionado en Geometría de los cuerpos sólidos (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí …   Wikipedia Español

  • Geometría absoluta — Se llama geometría absoluta al sistema axiomático que depende de los primeros cuatro postulados de Euclides, y no del quinto postulado, es decir, el de las rectas paralelas. Engloba, por tanto, la parte común de la geometría euclídea y la… …   Wikipedia Español

  • Lúnula (geometría) — En geometría se denomina lúnula a cualquiera de las dos figuras con forma semejante a la de una luna creciente obtenidas mediante la intersección de dos círculos. La palabra lúnula deriva del latín lunŭla, diminutivo de luna.[1] Contenido 1… …   Wikipedia Español

  • Trigonometría esférica — Triángulo esférico trirectángulo (sus ángulos suman : 270°). La trigonometría esférica es la parte de la geometría esférica que estudia los polígonos que se forman sobre la superficie de la esfera, en especial, los triángulos. La resolución… …   Wikipedia Español

  • Modelos de geometría no euclidiana — Los modelos de geometría no euclidiana son modelos matemáticos de geometría que no cumplen el quinto postulado de Euclides, el que establece que dos rectas paralelas son equidistantes. En los modelos geométricos hiperbólicos (geometría… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”