Esfera

Para otros usos de este término, véase Esfera (desambiguación).

Proyección en dos dimensiones de una esfera definida mediante paralelos y meridianos.

En geometría, una esfera es un cuerpo geométrico limitado por una superficie curva cerrada cuyos puntos equidistan de otro interior llamado centro de la esfera.

La esfera, como sólido de revolución, se genera haciendo girar una superficie semicircular alrededor de su diámetro (Euclides, L. XI, def. 14).

Esfera proviene del término griego σφαῖρα, sphaîra, que significa pelota (para jugar). Coloquialmente hablado, se emplean palabras como bola, globo (globo terrestre), etc., para describir un volumen esférico.

Volumen

Datos para hallar el área y volumen de la esfera respecto del cilindro circunscrito.

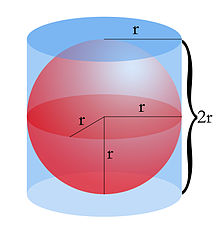
El volumen de una esfera es 2/3 del volumen del cilindro circunscrito a la esfera. Su base es un círculo del mismo diámetro que la esfera. Su altura tiene la misma medida que dicho diámetro:

$V = \frac{2}{3} (\pi r^2 \cdot 2r)$

$V = \frac{4\pi r^3}{3}$

donde V es el volumen de la esfera y r el radio.

Esta relación de volúmenes se adjudica a Arquímedes.

Es posible calcular el volumen de una esfera con un margen de error menor al 0.05% sin utilizar el valor de π:

$V = \frac{11}{21} (2r)^3$

Área

Arquímedes también demostró que el área de la esfera es dos tercios respecto al del cilindro. Entonces:

$A = \frac{2}{3} (2r \cdot 2\pi r + 2 \cdot \pi r^2)$

$A = \frac{2}{3} (4\pi r^2 + 2\pi r^2)$

$A = \frac{2}{3} (6\pi r^2)$

$\ A = 4\pi r^2$

El área de la esfera es también igual a la derivada de su volumen con respecto a r.

$V = \frac{4}{3}\pi r^3 = \int_{0}^{r}A(r) dr$

$\!4\pi r^2 = A(r).$

Ecuación cartesiana

En un sistema de coordenadas cartesianas en un espacio euclídeo tridimensional, la ecuación de la esfera unitaria (de radio 1), con centro en el origen, es:

$x^2 + y^2 + z^2 = 1\,$

Esta ecuación se obtiene considerando que en el punto M (x, y, z) de la esfera, el vector normal OM es igual a 1.

Generalizando, la esfera de radio r, de centro Ω (a, b, c) tiene como ecuación:

$(x - a)^2 + (y - b)^2 + (z - c)^2 = r^2\,$

La ecuación del plano tangente en el punto M (x', y', z') se obtiene mediante el desdoblamiento de las variables: en el caso de la esfera unitaria:

$x \cdot x' + y \cdot y' + z \cdot z' = 0\,$

y en el segundo ejemplo:

$(x - a) \cdot x' + (y - b) \cdot y' + (z - c) \cdot z' = 0\,$

Secciones

Sección de una esfera por un plano.

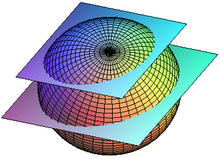
La intersección de un plano y una esfera siempre es un círculo. La esfera es el único volumen que tiene esta propiedad. Lógicamente, si el plano es tangente, el área de contacto queda reducido a un punto (puede considerarse el caso límite de la intersección).

Si el plano pasa por el centro de la esfera, el radio del círculo es el mismo que el de la esfera, r. En este caso, la circunferencia puede llamarse ecuador o círculo máximo.

Si la distancia d, entre el plano y el centro, es inferior al radio r de la esfera, aplicando el teorema de Pitágoras, el radio de la sección es:

$r' = \sqrt{r^2 - d^2}$

Intersección de esferas.

Por otra parte, dos esferas se intersecan si:

$d \le r + r'$

$r - r' \le d$

(son las desigualdades triangulares, y equivalen a que ningún lado es superior a la suma de los otros dos), es decir, si existe un triángulo con lados que midan r, r' y d, donde d es la distancia entre los centros de las esferas, r y r' sus radios.

En tal caso, la intersección es también una circunferencia. Cuando una de las desigualdades anteriores es una igualdad, la intersección será un punto, que equivale a una circunferencia de radio cero.

En general, el radio es:

$\frac 2 d \sqrt{m(m-r)(m-r')(m-d)} \quad \mbox{ con } \quad m = \frac {r+r'+d} 2$ el medio perímetro.

Coordenadas sobre la esfera

Para localizar un punto de la superficie esférica, las coordenadas cartesianas no son las más adecuadas, por varias razones: en primer lugar, porque hay tres coordenadas cartesianas, mientras que la superficie esférica es un espacio bidimensional. En segundo lugar, tratándose de una esfera, el ángulo es un concepto más adecuado que las coordenadas ortogonales.

Los dos orígenes angulares de las coordenadas esféricas

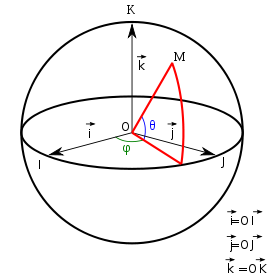
Se elige un ecuador y un punto del mismo como origen de los ángulos horizontales; se escoge una orientación del ecuador para definir el signo del ángulo φ; se escoge uno de los dos puntos de la esfera más distantes del ecuador –llamados polos– para definir el signo del ángulo θ.

Determinación de los puntos mediante ángulos

Todo punto de la esfera está localizado de manera inequívoca por los dos ángulos θ y φ. Con el valor de un ángulo sobre el plano horizontal (plano del ecuador) y otro vertical (desde un polo), se puede localizar cualquier punto de la esfera.

En geometría, normalmente, se expresan estos ángulos en radianes (pues permite calcular longitudes de arcos de circunferencia), mientras que en geografía se usan los grados sexagesimales o centesimales: en este caso, θ es la latitud del punto y φ su longitud si se toma un origen en el punto del ecuador del meridiano de Greenwich y el otro origen en el polo norte. Las latitudes positivas corresponden al hemisferio norte, y las longitudes positivas al hemisferio Este.

Introducir un tercer parámetro r permite localizar cualquier punto del espacio con las coordenadas esféricas (r, φ, θ). Si se impone tomar φ en un intervalo semi-abierto de longitud 2π y θ en uno de longitud π, entonces, cualquier punto del espacio tiene coordenadas esféricas únicas, salvo los del eje vertical, donde sirve cualquier valor de φ.

Las coordenadas cartesianas (x, y, z) en el sistema de coordenadas esféricas (r, φ, θ) serán:

$\left\{ \begin{matrix} x & = & r \sin \theta \; \cos\phi \\ y & = & r \sin \theta \; \mbox{sin }\phi\\ z & = & r \cos \theta \end{matrix} \right. \qquad \mbox{con }- \frac {\pi} 2 < \theta \le \frac {\pi} 2,\ \ \mbox{ y } \ \ 0 < \phi \le \pi$

Recíprocamente, a partir de las coordenadas cartesianas, se obtienen las coordenadas esféricas:

$\left\{ \begin{matrix} r = \sqrt{x^2 + y^2 + z^2} \ne 0 \\ \theta = \mbox{ arccos } \frac z r = \mbox{ arccos } \frac z {\sqrt{x^2 + y^2 + z^2}} \\ \phi = \mbox{ arcsin } \frac y {r \cos \theta} = 2 \mbox{ arcsin } \frac y {\sqrt{x^2+y^2} + x} \end{matrix} \right.$

Generalizaciones de la esfera

Esferas en dimensiones superiores

Se puede generalizar la noción de esfera en espacios vectoriales de dimensiones superiores a tres. A partir de la cuarta dimensión ya no es representable gráficamente, pero la definición sigue siendo que la esfera es el conjunto de los puntos equidistantes de un punto fijo. En un espacio euclídeo de cuatro dimensiones, usando un sistema de coordenadas cartesianas la ecuación de la esfera de radio 1 centrada en el origen es:

$x^2 + y^2 + z^2 + t^2 = 1\,$

donde t es la cuarta coordenada. Análogamente en un espacio euclídeo de n dimensiones:

$x_1^2 + x_2^2 + x_3 ^2 + \cdots + x_n^2 = 1$

Y para una esfera de radio r, y centro (c₁, c₂, ..., c_n):

$(x_1 - c_1)^2 + (x_2 - c_2)^2 + (x_3 - c_3)^2 + \cdots + (x_n - c_n)^2 = r^2$

El volumen de la esfera contenida en la superficie anterior, en dimensión n se calcula por inducción sobre n. Aquí están los diez primeros valores de V_n(r) y las superficies correspondientes:

Dimensión	1	2	3	4	5	6	7	8	9	10
Volumen	2r	πr²	4πr³ 3	π²r⁴ 2	8π²r⁵ 15	π³r⁶ 6	16π³r⁷ 105	π⁴r⁸ 24	32π⁴r⁹ 945	π⁵r¹⁰ 120
Superficie	2	2πr	4πr²	2π²r³	8π²r⁴ 3	π³r⁵	16π³r⁶ 15	π⁴r⁷ 3	32π⁴r⁸ 105	π⁵r⁹ 12

El volumen de la bola alcanza su máximo en dimensión 5, mientras que la superficie de la esfera lo alcanza en dimensión 7.

Derivación de la fórmula del n-volumen

Las ecuaciones de volumen pueden ser probadas por inducción matemática. En efecto, si llamamos V_n el volumen de la esfera unitaria (r = 1) en dimensión n. Entonces la integral de Wallis:

$V_{n+1} = I_{n+1} V_{n} \ \mbox{ con } \ I_n = 2\int_0^{\frac {\pi} 2} \mbox{sen}^n \ t \ dt$

Por una integración por partes, se obtiene la relación:

$I_n = \frac {n-1} n I_{n-2}$

lo que permite calcular los I_n también por inducción, conociendo I₀ e I₁.

La función gamma Γ íntimamente relacionada con los factoriales permite expresar sin inducción el volumen de una esfera de radio r en dimensión n.

$V_n(r) = \frac {\pi^{\frac n 2} r^n} {\Gamma (\frac n 2 +1)}$

Existe la posibilidad de representar una n-esfera o hiperesfera de n dimensiones como fibrado de otra hiperesfera de dimensión inferior. Esto sólo sucede en tres casos:

$S^3\;$ , puede ser representada como fibrado no trivial con espacio base $S^2\;$ y fibra $S^1\;$ , esta construcción puede obtenerse a partir de una construcción geométrico-algebraica utilizando números complejos.
$S^7\;$ , puede ser representada como fibrado no trivial con espacio base $S^4\;$ y fibra $S^3\;$ , esta construcción puede obtenerse a partir de una construcción geométrico-algebraica utilizando números cuaterniónicos.
$S^{15}\;$ , puede ser representada como fibrado no trivial con espacio base $S^8\;$ y fibra $S^7\;$ , esta construcción puede obtenerse a partir de una construcción geométrico-algebraica utilizando números octoniónicos.

Para dimensión superior no existen otros casos en que esto sea posible.^[1]

Esferas en otras métricas

La noción de esfera se generaliza a cualquier espacio métrico (E,d) así: la esfera de centro a y de radio r es el conjunto $\scriptstyle S(a, r) = \{x\in E, d(a, x) = r \}$ , y la bola correspondiente es $\scriptstyle B(a, r) = \{ x\in E, d(a, x) \le r\}$ .

Para no ser demasiado general, restrinjámonos al espacio real tridimensional, con distancias provenientes de distintas normas, y consideramos las esferas unitarias.

Para un vector u(x, y, z) cualquiera, se definen las normas siguientes:

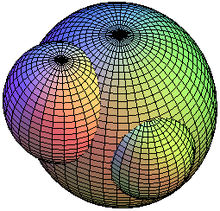
||u||₁ = |x| + |y| + |z|. S(O,1) es un octaedro regular (figura a la derecha).

||u||₂ = √(x² + y² + z²). Se trata de la norma euclidiana, luego S(O,1) es la esfera usual.

||u||₃ = ³√(|x|³ + |y|³ + |z|³). S(0,1) es una especie de forma intermedia entre la esfera usual y el cubo (figura a la izquierda). ||u||_∞ = max(|x|,|y|,|z|). S(0,1) es un cubo.

Esferas en topología

Cabe tener presente que el concepto geométrico y el concepto topológico de "n-esfera" no coinciden. En geometría, la superficie de la esfera es llamada 3-esfera, mientras que los topólogos se refieren a ella como 2-esfera y la indican como $S^2\;$ .^[2]

Esferas en física

Una de las esferas más perfectas creadas, refractando la imagen de Albert Einstein. Se aproxima a la esfera ideal con un error menor que el tamaño de cuarenta átomos alineados.

La esfera es la figura geométrica que para igual volumen presenta la superficie externa menor. Esta propiedad es la causa de su omnipresencia en el mundo físico: en una gota de un líquido inmerso en un ambiente gaseoso, o entre líquidos no solubles de diferente densidad, existen fuerzas superficiales que deformarán la gota hasta encontrar el valor mínimo de tensión en todos los puntos de la misma, y este corresponde a una esfera, en ausencia de toda perturbación exterior.

Véase también

Referencias

↑ R. Penrose: El camino de la realidad, Ed. Debate, Barcelona, 2006, p. 464, ISBN 84-8306-681-5.
↑ Weisstein, Eric W. «Esfera» (en inglés). MathWorld. Wolfram Research.

Bibliografía

Roger Penrose (2005): The Road to Reality: A Complete Guide to the Laws of the Universe.
William Dunham. "Pages 28, 226", The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems and Personalities, ISBN 0-471-17661-3.

Enlaces externos

Wikimedia Commons alberga contenido multimedia sobre Esfera. Commons

El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.

Categorías:

Figuras geométricas
Superficies
Geometría elemental

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Sinónimos:

globo, bola, pelota, balón / cielo, firmamento, espacio, universo / clase, nivel, categoría, círculo, ambiente

Mira otros diccionarios:

esfera — (Del lat. sphaera, y este del gr. σφαῖρα). 1. f. Geom. Sólido terminado por una superficie curva cuyos puntos equidistan todos de otro interior llamado centro. 2. Geom. Superficie de este sólido. 3. Círculo en que giran las manecillas del reloj.… … Diccionario de la lengua española
esfera — sustantivo femenino 1. Área: geometría Cuerpo geométrico limitado por una superficie curva cuyos puntos equidistan todos de otro interior llamado centro: La superficie de la esfera se calcula con una fórmula sencilla. 2. Círculo o superficie en… … Diccionario Salamanca de la Lengua Española
esfera — |é| s. f. 1. Corpo redondo cujos pontos superficiais estão equidistantes do centro; bola. 2. Representação geográfica da Terra (esfera terrestre). 3. Representação dos círculos da esfera celeste (esfera armilar). 4. Zona da esfera terrestre.… … Dicionário da Língua Portuguesa
esfera — Objeto redondeado, con forma de globo, generado técnicamente por un círculo que rota alrededor de un diámetro considerándolo como su eje. Diccionario Mosby Medicina, Enfermería y Ciencias de la Salud, Ediciones Hancourt, S.A. 1999 … Diccionario médico
Esfera — (Del lat. sphaera < gr. sphaira, pelota.) ► sustantivo femenino 1 GEOMETRÍA Cuerpo o espacio limitado por una superficie curva cuyos puntos equidistan todos de otro interior llamado centro. 2 Círculo en el que giran las manecillas del reloj: ■ … Enciclopedia Universal
esfera — {{＃}}{{LM E16048}}{{〓}} {{SynE16467}} {{［}}esfera{{］}} ‹es·fe·ra› {{《}}▍ s.f.{{》}} {{＜}}1{{＞}} Cuerpo geométrico limitado por una superficie curva cuyos puntos están todos a la misma distancia del punto interior llamado centro: • Una bola de… … Diccionario de uso del español actual con sinónimos y antónimos
esfera — s f 1 (Geom) Superficie curva y cerrada cuyos puntos equidistan de otro llamado centro; sólido limitado por una superficie de esas características: el radio de una esfera 2 Esfera celeste Superficie ideal, curva y cerrada, concéntrica a la Tierra … Español en México
esfera — (f) (Intermedio) cuerpo geométrico de superficie curva, cuyos puntos están todos a igual distancia del centro Ejemplos: La Tierra no es una esfera perfecta. Los balones tienen forma de esfera. Sinónimos: círculo … Español Extremo Basic and Intermediate
esfera — f. Sólido de superficie curva cuyos puntos equidistan del centro. Círculo en que giran las agujas del reloj. Clase, condición de una persona; celeste, esfera ideal, concéntrica con la terrestre, en la que aparentemente se mueven los astros … Diccionario Castellano
Esfera de Dyson — Saltar a navegación, búsqueda Corte de una «concha de Dyson», variación de la idea original de esfera de Dyson con un radio de 1 UA. Una esfera de Dyson es una hipotética megaestructura propuesta en 1960 por el físico Freeman Dyson, en un … Wikipedia Español