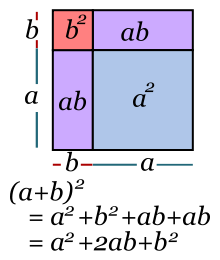
Trinomio cuadrado perfecto

Trinomio cuadrado perfecto
Commons-emblem-question book orange.svg
 Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas.
Puedes añadirlas así o avisar al autor principal del artículo en su página de discusión pegando: {{subst:Aviso referencias|Trinomio cuadrado perfecto}} ~~~~
Se ha sugerido que Trinomio sea fusionado en este artículo o sección (discusión).
Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí.
Visualización de la fórmula para un binomio al cuadrado y para su trinomio cuadrado perfecto

Un Trinomio Cuadrado Perfecto, por brevedad TCP, es un polinomio de tres términos que resulta de elevar al cuadrado un binomio.

Todo trinomio de la forma:
(a+b)^2 = a^2+2ab+b^2 \,\!
es un trinomio cuadrado perfecto ya que
(a+b)^2=(a+b)(a+b)= \,\!
=a^2+ab+ab+b^2=a^2+2ab+b^2 \,\!

Siendo la regla: Cualquier suma de binomios al cuadrado es igual al cuadrado del primer término, más el doble del primer por el segundo término, más el cuadrado del segundo término. De lo anterior resulta que un trinomio será cuadrado perfecto siempre que se cumplan las siguientes condiciones:

  1. El polinomio pueda ser ordenado en potencias descendentes de una variable.
  2. Dos de los términos son cuadrados perfectos.
  3. El otro término es el doble producto de las raíces cuadradas de los demás.
  4. El primer y tercer término deben de tener el mismo signo

Un trinomio cuadrático general de la forma ax^2+bx+c \,\! es un TCP si se cumple que el discriminante es cero, es decir, que la cantidad b^2-4ac \,\! es siempre igual a 0 \,\!.

También se considera un trinomio cuadrado perfecto de la forma: a^2-2ab+b^2 \,\!, donde las mismás reglas explicadas anteriormente aplican.

Fórmula

Para convertir un binomio en un Trinomio Cuadrado Perfecto (TCP), es necesario aplicar la siguiente fórmula, la primera cantidad elevada al cuadrado más 2 veces la primera cantidad por la segunda más la segunda cantidad elevada al cuadrado.

A^2+2AB+B^2=(A+B)^2

Ejemplo:

(2a+3b)^2 \,\!

Aplicamos la fórmula:

(2a+3b)^2 = (2a)^2+2 (2a) (3b)+(3b)^2 \,\! =
4a^2+12ab+9b^2 \,\!

Para revertir el TCP a la suma de binomios al cuadrado original, es necesario hallar la raíz cuadrada de los dos primeros términos:

4a^2+12ab+9b^2 = \left(\sqrt{4a^2}+\sqrt{9b^2} \right)^2 = (2a+3b)^2 \,\!

Así queda demostrada la fórmula

Ejemplos

Sea:

12xy+9x^2+4y^2 \,\!

Ordenando según las normas del álgebra, de más a menos x \,\!, resulta que:

9x^2+12xy+4y^2 \,\!

Y podemos darnos cuenta de:

9x^2=(3^2)(x^2)=(3x)^2 \,\!
4y^2=(2y)^2 \,\!
12xy=2(3x)(2y) \,\!

Podemos averiguar que es un TCP ya que cumple con las normas:

12xy+9x^2+4y^2 = \left(\sqrt{9a^2}+\sqrt{4b^2} \right)^2 = (3x+2y)^2 \,\!

Sea:

\frac{1}{4}y^4z^2+w^2+wy^2z \,\!

Ordenando respecto a la variable de mayor potencia (y) tenemos:

\frac{1}{4}y^4z^2+wy^2z+w^2 \,\!

evaluando el trinomio vemos que:

\frac{1}{4}y^4z^2=\left(\frac{1}{2}y^2z\right)^2 \,\!

y

w^2=(w)^2 \,\!

por último vemos que

2\left(\frac{1}{2}y^2z\right)(w)=wy^2z \,\!

Entonces la expresión es un trinomio cuadrado perfecto.

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Cuadrado perfecto — ► locución MATEMÁTICAS Número que es el producto de multiplicar un número entero por sí mismo. * * * Un cuadrado perfecto es un número cuya raíz cuadrada es un número entero. Algunos cuadrados perfectos o raíces cuadradas exactas son: ● 2²=4 ● 3² …   Enciclopedia Universal

  • Trinomio — En álgebra, un trinomio es un polinomio con tres términos: la suma de tres monomios. Trinomio cuadrado perfecto Artículo principal: Trinomio cuadrado perfecto Surge de elevar al cuadrado dos términos: Véase también Productos notables… …   Wikipedia Español

  • Completando el cuadrado — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Factorización — Saltar a navegación, búsqueda En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos… …   Wikipedia Español

  • Productos notables — es el nombre que reciben aquellas multiplicaciones con expresiones algebraicas cuyo resultado puede ser escrito por simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la… …   Wikipedia Español

  • Binomio — Saltar a navegación, búsqueda En álgebra, un binomio es una expresión algebraica con dos términos. Estrictamente hablando se refiere a un polinomio formado por la suma de dos monomios, aunque se usa de forma más fácil para indicar cualquier… …   Wikipedia Español

  • Ecuación de segundo grado — Saltar a navegación, búsqueda Los puntos comunes de una parábola con el eje X (recta y=o), si los hubiese, son las soluciones reales de la ecuación cuadrática. Una ecuación de segundo grado o ecuación cuadrática es una ecuación polinómica donde… …   Wikipedia Español

  • Función polinómica de grado 2 — Saltar a navegación, búsqueda De vital importancia en matemáticas y física es la función cuadrática o de segundo grado. Una función polinómica de grado dos o función cuadrática es la que corresponde a un polinomio en x de segundo grado, según la… …   Wikipedia Español

  • Función cuadrática — En matemáticas, una función cuadrática o función de segundo grado es una función polinómica de grado dos definida como: Gráficas de funciones cuadráticas. en donde a, b y c son números reales (constantes) y a es …   Wikipedia Español

  • Ecuación de tercer grado — Gráfica de una función cúbica. Una ecuación de tercer grado con una incógnita es una ecuación que se puede poner bajo la forma canónica: , donde a, b, c y d (a ≠ 0) son números que pertenecen a un campo, usualmente el …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”