Ecuación de tercer grado

Ecuación de tercer grado
Gráfica de una función cúbica.

Una ecuación de tercer grado con una incógnita es una ecuación que se puede poner bajo la forma canónica:

ax^3 + bx^2 + cx + d = 0 \,,

donde a, b, c y d (a ≠ 0) son números que pertenecen a un campo, usualmente el campo de los números reales o el de los números complejos.

Contenido

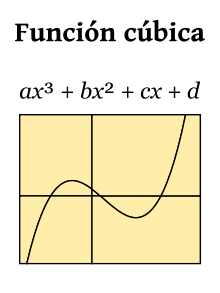
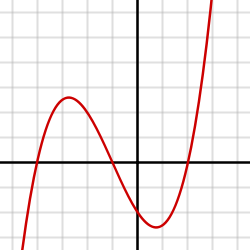
Función cúbica

La función cúbica es una función polinómica de tercer grado. Tiene la forma:

f(x) = ax^3 + bx^2 + cx + d \, ; donde el coeficiente a es distinto de 0.

Tanto el dominio de definición como el conjunto imagen de estas funciones pertenecen a los números reales.

El caso general

Sea K \, un cuerpo conmutativo, donde se pueden extraer raíces, propiedad que hará posible resolver la ecuación.

En un cuerpo algebraicamente cerrado se sabe que todo polinomio de tercer grado (o ecuación cúbica) tiene tres raíces. Este es el caso, por ejemplo, del cuerpo de los números complejos, según el Teorema Fundamental del Álgebra.

La solución de la ecuación algebraica cúbica fue dada por primera vez en el libro Ars Magna (del latín, que significa Gran Arte o Arte Magno) por el matemático italiano Gerolamo Cardano (1501-1576) que publicó en el año de 1545, razón por la cual se le llama método de Cardano.

Los pasos de la resolución son:

  • Dividir la ecuación inicial por el coeficiente a (a ≠ 0). Se obtiene:
x^3 + b'x^2 + c'x + d' = 0 \, con b' = \frac {b} {a} \,, c' = \frac {c} {a} \,, d' = \frac {d} {a} \,.
  • Proceder al cambio de incógnita z = x + \frac {b'} {3} \,, para suprimir el término cuadrado. En efecto, al desarrollar \left ( z - \frac {b'} {3} \right )^3 \, con la identidad precedente, vemos aparecer el término -b'z^2 \,, compensado exactamente por b'z^2 \, que aparece en b' \left ( z - \frac {b'} {3} \right )^2 \,. Se obtiene:
z^3 + pz + q = 0 \,, con p y q números del cuerpo que tienen las siguientes expresiones
p = c'-\frac{b'^2}{3} \,
q = \frac{2b'^3}{27} - \frac{b'c'}{3} + d' \,.
  • Y ahora, la astucia genial: escribir z = u + v \,. Así, la ecuación precedente da (u + v)^3 + p(u + v) + q = 0 \,.
Desarrollando: u^3 + 3u^2v + 3uv^2 + v^3 + pu + pv + q = 0 \,.
Reagrupando: (u^3 + v^3 + q) + (3uv^2 + 3u^2v + pu + pv) = 0 \,.
Factorizando: (u^3 + v^3 + q) + (u + v)(3uv + p) = 0 \,.
Como se ha introducido una variable adicional (u y v en vez de z), es posible imponerse una condición adicional. Concretamente:
3uv + p = 0 \,, que implica u^3 + v^3 + q = 0 \,.
  • Pongamos U = u^3 \, y V = v^3 \,. Entonces tenemos U + V = - q \, y UV = -\frac {p^3} {27} \, porque UV = (uv)^3 = (-\frac {p} {3})^3 \,. Por lo tanto U y V son las raíces de la ecuación auxiliar X^2 + qX - \frac {p^3} {27}=0\,, que se sabe resolver.

Luego u\, y v\, son raíces cúbicas de U\, y V\, (que verifican uv = -\frac {p} {3} \,), z = u + v \, y finalmente x = z - \frac {b'} {3} \,.

En el cuerpo \mathbb{C}, si u_0\, y v_0\, son estas raíces cúbicas, entonces las otras son \omega u_0\, y \omega^2u_0\,, y por supuesto \omega v_0\, y \omega^2v_0\,, con \omega = e^{\frac {2i \pi} {3}}\,, una raíz cúbica de la unidad.

Como el producto uv está fijado \left( uv = -\frac{p}{3} \right)\,, las parejas (u, v)\, posibles son (u_0, v_0)\,, (\omega u_0, \omega^2v_0)\, y (\omega^2u_0, \omega v_0)\,.

Las otras raíces de la ecuación de tercer grado son por lo tanto \omega u_0 + \omega^2v_0 - \frac {b'} {3} \, y \omega^2u_0 + \omega v_0 - \frac {b'} {3} \,.

Discriminante

Gráfico de una función cúbica del tipo y = K(x+4)·(x+1)·(x-2). Las raíces son los lugares donde la curva cruza el eje x (y = 0), esto es: x1 = -4, x2 = -1 y x3 = 2.

Resulta importante y a la vez esencial obtener propiedades elementales de los polinomios como herramientas de análisis en los resultados según los valores de sus coeficientes.

  • Demostración de la discriminante \Delta = (4p^3 + 27q^2)\, mediante transformaciones de equivalencia de la ecuación auxiliar X^2 + qX - \frac {p^3} {27}=0\,
Trinomio cuadrado perfecto X^2 + qX + \frac {q^2} {2^2}=0\,
Trasformación equivalente X^2 + qX - \frac {p^3} {27}=0\, en X^2 + qX - \frac {p^3} {27} + \frac {q^2} {2^2} = \frac {q^2} {2^2}\,
Moviendo - \frac {p^3} {27} al miembro derecho X^2 + qX + \frac {q^2} {2^2} = \frac {q^2} {2^2}\ + \frac {p^3} {27}
Demostrado que X^2 + qX - \frac {p^3} {27}= \frac {q^2} {4}\ + \frac {p^3} {27} = (4p^3 + 27q^2) = 0 cuando la ecuación posee raices Reales dobles.

El caso real

Las primeras ecuaciones de tercer grado que se intentó resolver fueron con coeficientes reales (de hecho: enteros). El cuerpo de los reales no es algebraicamente cerrado, por lo tanto, el número de raíces reales no es siempre 3. Las que faltan se encuentran en C, extensión algebraica cerrada de R. La distinción aparece cuando se sacan las raíces cuadradas en el cálculo de U y V. Las raíces cúbicas no plantean problemas.

Se demuestra que el número de raíces reales depende del discriminante de la ecuación auxiliar \Delta = (4p^3 + 27q^2)\,:

  • Si Δ > 0 existe una única raíz real. Las demás son complejas conjugadas.
  • Si Δ = 0 existe una raíz múltiple real: una raíz triple o una doble y otra simple, todas reales.
  • Si Δ < 0 existen tres raíces reales.

Habrán notado que siempre hay por lo menos una solución real. Es debido a que las funciones polinomiales no constantes tienen límites infinitos en +∞ y -∞ y las de grado impar tienen límites de signos contrarios. Como son funciones contínuas, tienen que pasar por cero, por el teorema de los valores intermedios.

En la figura siguiente se registra todos los casos, según los signos de a y de Δ.

Aunque lo más fácil es resolverla con el método Newton-Raphson ya que sabemos que al menos habrá una solución real.

Raíces reales de la ecuación cúbica

La ecuación cúbica incompleta z^3+pz+q=0 \, posee tres raíces reales cuando el discriminante D<0 \,, pero donde p<0 \, y q \, posee cualquier valor y signo. Tales raíces se calculan como

z_{k+1}=\pm2 \sqrt{\frac{-p}{3}}\cos(\frac{\Phi}{3}+120k) , para k = 0, 1, 2 \,

donde el signo positivo se usa si q\leq0 \, y el signo negativo se usa si q>0 \,. Mientras que \phi \, esta dada por

\Phi=\arccos{\sqrt{\frac{q^2/4}{-p^3/27}}}

De modo que si queremos calcular las tres raíces de la ecuación cúbica completa ax^3+bx^2+cx+d=0 \,, entonces podemos obtenerlas fácilmente como

x_{k}=z_{k}-\frac{b}{3a} , para k = 1, 2, 3 \,

Raíces múltiples

En cualquier ecuación cúbica es posible que se presenten raíces múltiples, es decir, raíces de multiplicidad dos y tres, esto es, que dos o tres de las raíces sean iguales entre sí. Las raíces de multiplicidad unitaria ya fueron descritas antes, ahora la raíz doble se puede presentar si y sólo si se cumple la condición de que

D=0, p\not=0, q\not=0 \,

y las raíces de la ecuación cúbica incompleta serán

z_{1}=2u=2v=-2z_{2}=-2z_{3} \,

mientras que las raíces triples se presentan cuando se cumpla la condición de que

D=p=q=0 \,

con lo que las raíces de la ecuación cúbica completa se calcularán fácilmente como

x_{1}=x_{2}=x_{3}=\frac{-b}{3a} \, .

Ejemplo 1

Sea la ecuación cúbica 2t^3 + 6t^2 + 12t + 10 = 0 \,, procedamos a resolverla. Para ello, sigamos los pasos descritos en el primer párrafo.

  • t^3 + 3t^2 + 6t + 5 = 0 \, (al dividir por 2)
  • Con x = t + 1, es decir t = x - 1, reemplazando: (x - 1)^3 + 3(x - 1)^2 + 6(x - 1) + 5 = 0 \,, y desarrollando: x^3 + 3x + 1 = 0 \,
  • x = u + v, U = u³, V = v³ y nos imponemos U + V = - 1 y UV = - 1. U y V son las raíces de X² + X - 1 = 0.
U = \frac {-1 - \sqrt {5}} {2} \, y V = \frac {-1 + \sqrt {5}} {2} \,, luego u = \sqrt[3]{\frac {-1 - \sqrt {5}} {2}} \, y v = \sqrt[3]{\frac {-1 + \sqrt {5}} {2}} \,.
t = x - 1 = u + v - 1 = \sqrt[3]{\frac {-1 - \sqrt {5}} {2}} + \sqrt[3]{\frac {-1 + \sqrt {5}} {2}} - 1 \approx -1,3221853546

Segundo ejemplo

Este ejemplo es histórico porque fue el que tomó Rafael Bombelli quien fue, con Cardano, el primero en resolver ecuaciones del tercer y cuarto grado por el método ya expuesto (en la Italia del renacimiento, en pleno siglo XVI).

La ecuación es x³ - 15x - 4 = 0.

Estudiando la función x → x³ - 15x - 4 o calculando el discriminante Δ = -13068 < 0, nos damos cuenta que esta ecuación tiene tres raíces ( vean el cuadro 3 de la figura). Por lo tanto debería ser más fácil que en el primer ejemplo encontrar una.

Los dos primeros pasos son inútiles. Pasamos al tercero: x = u + v, U = u³, V = v³.

U + V = 4 y UV = 125

U y V son las raíces de X² - 4X + 125 = 0, ecuación cuyo discriminante ya hemos calculado y que es negativo. Por lo tanto no tiene raíces reales. Este método nos permite encontrar las raíces, todas reales, pasando obligatoriamente por los complejos. ¡ Es paradójico !

Esta constatación fue un argumento a favor de los complejos: son herramientas imprescindibles para resolver ecuaciones, aunque sólo tengan soluciones reales.

Hallamos U = 2 - 11·i y V = 2 + 11·i. Extraer raíces cúbicas en los complejos no es lo mismo que en los reales. Hay dos métodos: uno geométrico, que utiliza el argumento y el módulo (se divide el argumento por tres, y se toma la raíz cúbica del módulo), y otro algebraico, que emplea las partes real e imaginaria: Pongamos u = a + bi.

u³ = 2 - 11i equivale al sistema:
a³ - 3ab² = 2 (parte real)
3a²b - b³ = - 11 (parte imaginaria)
a² + b² = 5 (módulo)

Obtenemos a = 2 y b = -1, o sea u = 2 - i, y v es su conjugado: v = 2 + i.

En conclusión, x = u + v = (2 - i) + (2 + i) = 4, lo que se verifica de inmediato.

Las otras raíces son x' = j(2 - i) + j²(2 + i) = - 2 + √3 y x" = j²(2 - i) + j(2 + i) = - 2 - √3.

Cuando Δ es negativo, U y V son conjugados, y por lo tanto también lo son u y v (con tal de bien escoger la raíz cúbica, recordando que uv = -p/3); así estamos seguros de obtener un x real, y de hecho también x' y x".

Nota: Toda ecuación cúbica completa tiene otra equivalente incompleta o completa condicionada (familia de cúbicas), que se puede observar mediante el cambio de variable x=z+k. Con esto podemos encontrar otra fórmula general para las ecuaciones cúbicas, diferente a las fórmulas de Cardano o Tartaglia.

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Ecuación de tercer grado — Una ecuación de tercer grado con una incógnita es una ecuación que se puede poner bajo la forma canónica: , donde a, b, c y d (a ≠ 0) son números que pertenecen a un cuerpo, usualmente a R o a C …   Enciclopedia Universal

  • Ecuación de segundo grado — Saltar a navegación, búsqueda Los puntos comunes de una parábola con el eje X (recta y=o), si los hubiese, son las soluciones reales de la ecuación cuadrática. Una ecuación de segundo grado o ecuación cuadrática es una ecuación polinómica donde… …   Wikipedia Español

  • Ecuación de cuarto grado — Saltar a navegación, búsqueda Gráfico de una ecuación de cuarto grado. Una ecuación cuártica con una incógnita es una ecuación que se puede poner bajo la forma canónica …   Wikipedia Español

  • Ecuación de quinto grado — Saltar a navegación, búsqueda Polinomio de 5º grado: f(x) = (x+4)(x+2)(x+1)(x 1)(x 3)/20+2 En matemática, se denomina ecuación quíntica o de quinto grado a una ecuación polinómica en que el exponente de la variable independiente de mayor grado es …   Wikipedia Español

  • Ecuación — Saltar a navegación, búsqueda Una ecuación es una igualdad entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, y desconocidos o incógnitas, relacionados mediante operaciones matemáticas. Los… …   Wikipedia Español

  • Grado (matemática) — Este ártículo trata del grado tal y como es empleado en el área de las matemáticas. Para significados alternativos de esta palabra, véase grado. En matemáticas existen diferentes significados de la palabra grado dependiendo del área matemática de …   Wikipedia Español

  • grado — sustantivo masculino 1. Cada uno de los valores, medidas o estados de una cosa, que pueden ordenarse de mayor a menor o viceversa: Lo mejor de esta empresa es el grado de preparación de sus empleados. Está acusado de asesinato en primer grado.… …   Diccionario Salamanca de la Lengua Española

  • Grado — I (Del lat. gradus, graduación.) ► sustantivo masculino 1 Situación, valor, calidad o medida de una cosa: ■ todavía no sabemos cuál es el grado de complejidad de este asunto. SINÓNIMO nivel 2 Cada una de las partes de la escalera en la que se… …   Enciclopedia Universal

  • grado — grado1 (Del lat. gradus). 1. m. Cada uno de los diversos estados, valores o calidades que, en relación de menor a mayor, puede tener algo. Sufre quemaduras de primer grado. 2. Valor o medida de algo que puede variar en intensidad. En sumo grado.… …   Diccionario de la lengua española

  • grado — {{＃}}{{LM G19273}}{{〓}} {{SynG19769}} {{［}}grado{{］}} ‹gra·do› {{《}}▍ s.m.{{》}} {{＜}}1{{＞}} Voluntad o gusto: • Lo haré encantada y de buen grado.{{○}} {{＜}}2{{＞}} Cada uno de los estados, valores o calidades que, de menor a mayor, puede tener… …   Diccionario de uso del español actual con sinónimos y antónimos

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”