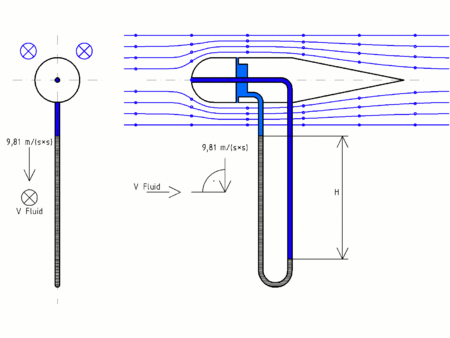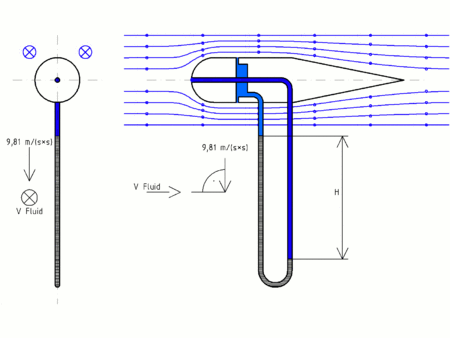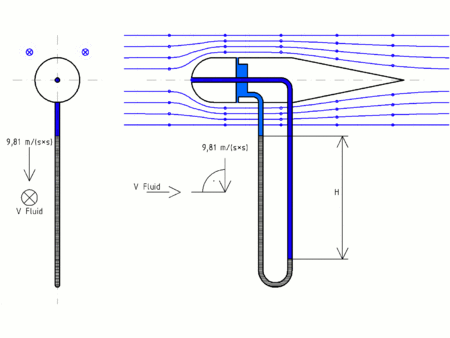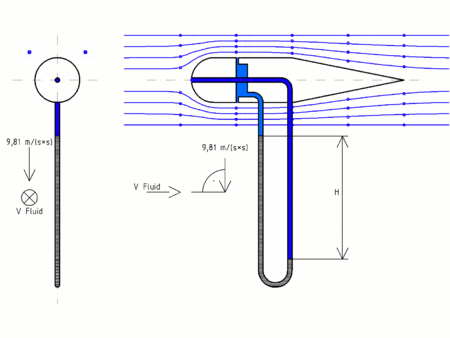
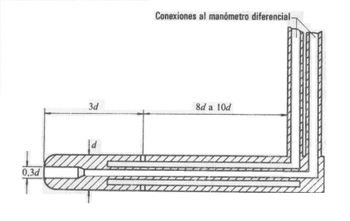
Tubo de Prandtl

Tubo de Prandtl: Corte esquemático de un tubo de Prandtl.

Corte esquemático de un tubo de Prandtl.

La idea de Ludwig Prandtl fue la de combinar en un solo instrumento un tubo de Pitot y un tubo piezométrico: El tubo de Pitot mide la presión total; el tubo piezométrico mide la presión estática, y el tubo de Prandtl mide la diferencia de las dos, que es la presión dinámica.

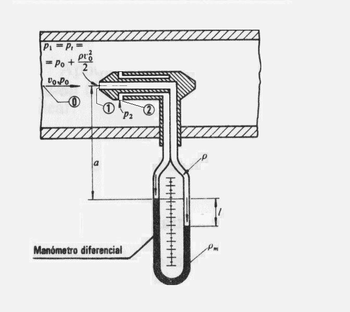
En el croquis se aprecia esquemáticamente, un tubo de Prandtl inmerso en un fluido de densidad $ρ$ , conectado a un manómetro diferencial cuyo líquido manométrico tiene densidad $ρ m$ .

El tubo de Prandtl, al igual que el tubo de Pitot, al ser introducido en el fluido en movimiento, produce una perturbación que se traduce en la formación en el de un punto de estancamiento, de manera que:

$\ p_1 = p_t$

$\ v_1 = 0$

En el punto 0 la corriente no perturbada tiene la presión $\ p_0$ y la velocidad $\ v_0$ que es la que se quiere medir.

El punto 1 es la entrada del tubo de Pitot, y el punto 2, donde se indica en la figura. En el punto 2 lo que se tiene es un tubo piezométrico, con varias entradas laterales interconectadas que no perturban la corriente y que por lo tanto miden la presión estática.

Despreciando las diferencias de altura de velocidad y geodésica entre los puntos 0 y 2 que suele ser muy pequeña por ser el tubo muy fino, y estar la corriente en 2 prácticamente normalizada después de la perturbación en 1, se tiene, despreciando también las pérdidas:

$\ v_2 = v_{0t}$

$\ p_2 = p_0$

Donde: $\ v_{0t}$ = velocidad teórica en la sección 0.

La ecuación de Bernoulli entre 0 y 1 ( $\ z_0 = z_1$ , $\ v_1 = 0$ - punto de estancamiento)

${p_0 } + \rho . {v_{0t}^2 \over 2} = {p_1 }$ y expresado de otra forma: ${p_1 } - {p_0 } = \rho . {v_{0t}^2 \over 2}$

Por otra parte yendo de 1 a 2 por el interior del manómetro, estando tanto el fluido principal como el fluido manométrico en reposo, se puede aplicar la ecuación fundamental de la hidrostática entre 1 y 2 ( $\ z_1$ ≈ $\ z_2$ ) de la siguiente forma:

$\ p_1 = p_2 + \rho . g. a + \rho _m . g . l- \rho . g . l - \rho . g . a$

De las ecuaciones anteriores se deduce:

$\ \rho . {v_{0t}^2 \over 2} = (\rho _m - \rho) . g . l$

(presión dinámica teórica, tubo de Prandtl)

Despejando se tiene:

$v_{0t} = {\sqrt {{2. g . l (\rho _m - \rho) \over {\rho}}}}$

En el caso particular de que la medición de velocidad se efectúe en un flujo de agua:

$v_{0t} = {\sqrt {{2. g . l (\delta - 1)}}}$

(velocidad teórica de la corriente, tubo de Prandtl)

Donde: $δ$ - densidad relativa del líquido manométrico.

Tubo de Prandtl estandarizado.

En la práctica $\ v_2$ es algo mayor que $\ v_0$ , y por lo tanto según la ecuación general de Bernoulli $\ p_2$ es algo menor que $\ p_0$ . Adicionalmente, en el punto 1, si el eje del tubo de Prandtl está inclinado con relación a las líneas de corriente, puede producirse una velocidad distinta de cero y por lo tanto una presión $\ p_1 < p_t$ . Se debe introducir por lo tanto un coeficiente $\ C_v$ . , llamado coeficiente de velocidad del tubo de Prandtl, que tiene valores próximos a 1, determinados experimentalmente en laboratorio.

La velocidad real $\ v_0$ será determinada, para el agua, por la expresión:

$v_{0} = C_v . {\sqrt {{2. g . l (\delta - 1)}}}$

Véase también: Tubo de Pitot

Referencia

Mecánica de Fluidos y Máquinas Hidráulicas. Claudio Mataix Plana, 1982.

Categorías:
Hidráulica
Instrumentos de medición

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

Tubo Pitot — Diagrama del sistema pitot estatico , incluye el tubo pitot, los instrumentos pitot static, y las tomas de presión estáticas y dinámica … Wikipedia Español
Intercambiador de calor dinámico de superficie rascada — Un intercambiador de calor dinámico de superficie rascada es un dispositivo diseñado para intercambiar la máxima cantidad de calor por unidad de área mediante la generación de tanta turbulencia como sea posible. Contenido 1 Introducción 2… … Wikipedia Español
Helio — Hidrógeno ← Helio → Litio … Wikipedia Español
Ley de Poiseuille — La ley de Poiseuille (también conocida como ley de Hagen Poiseuille después de los experimentos llevados a cabo por Gotthilf Heinrich Ludwig Hagen (1797 1884) en 1839) es la ley que permite determinar el flujo laminar estacionario ΦV de un… … Wikipedia Español
Vorticidad — La figura muestra como se conserva la vorticidad si no hay viscosidad: si inicialmente era nula, cualquier variación encuentra en algún lado su variación opuesta. La vorticidad es una magnitud física empleada en mecánica de fluidos y en el mundo… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Tubo de Prandtl

Referencia

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Tubo de Prandtl

Referencia

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo