- Vorticidad
-
La vorticidad es una magnitud física empleada en mecánica de fluidos y en el mundo meteorológico para cuantificar la rotación de un fluido.
Contenido
Introducción: el campo de vorticidad
Matemáticamente la vorticidad es el campo vectorial definido por el rotacional del campo de movimiento:
(1)

El origen de la vorticidad y su importancia
La presencia de vorticidad en un fluido siempre implica la rotación de las partículas fluidas, acompañada o no de alguna deformación transversal. En un fluido real su existencia está íntimamente ligada a las tensiones tangenciales. La ecuación que permite estudiar la cinética de este campo (llamada ecuación de transporte de vorticidad) se obtiene tomando el rotacional a ambos lados de la ecuación de Navier-Stokes y expresando la derivada local en términos de la derivada substancial.
(2)

La vorticidad se origina fundamentalmente en los contornos sólidos debido a que los fluidos no son capaces de deslizar sobre ellos, y luego se propaga al interior del fluido siguiendo la ley de variación descripta por la Ecuación 2. El primer término corresponde a la variación de vorticidad por deformación de las líneas vorticosas. Este fenómeno ocurre tanto en fluidos viscosos como no viscosos, sin embargo es un hecho notable que cuando el fluido es no visco (ideal) esta es la única forma en que la vorticidad puede variar. Tal como lo demostró Kelvin en uno de sus teoremas, esta variación ocurre siempre de manera que el flujo de vorticidad asociado a una superficie abierta que se mueve con el fluido permanece constante, lo cual también implica que la variación de la circulación Γ de la velocidad a lo largo del contorno de esa misma superficie sea nula:
(3)

Para hallar una explicación simple a este mecanismo de variación de vorticidad imaginemos que en el interior de un fluido no viscoso se haya formado de alguna manera una región vorticosa en forma de tubo con sección variable en su longitud. Como dentro de él no existe difusión viscosa el flujo de vorticidad asociado a cualquier superficie transversal es idéntico y constante, por lo tanto al variar la sección debe haber una variación en la intensidad de la vorticidad.
El segundo término de la Ecuación 2, que a diferencia del primero sólo se evalúa en fluidos viscosos, corresponde a la variación de vorticidad por difusión viscosa y tiene analogía (similar ecuación diferencial) con el fenómeno de conducción de calor en sólidos. Debido a este fenómeno, partículas que no tienen vorticidad la adquieren de partículas vecinas que si la tienen, produciéndose una difusión de vorticidad hacia el interior del fluido.
Un ejemplo sencillo que evidencia este fenómeno es el de un recipiente cilíndrico lleno de fluido que parte del reposo y de repente comienza girar sobre su eje a una velocidad angular constante. Cualquier persona puede intuir que el fluido que originalmente permanecía inmóvil comenzará a girar junto con el recipiente. Primero lo hará en el contorno, pero al cabo de un determinado tiempo todo el fluido se encontrará rotando como si fuese una masa sólida dentro del recipiente. Lo que ocurre en el primer instante del experimento es justamente una generación de vorticidad debido a la aparición de un gradiente de velocidad transversal. Es decir: de repente las partículas del contorno se hallan girando con el recipiente debido a su adherencia, mientras que sus vecinas aun permanecen inmóviles. Lo que ocurre a continuación es una progresiva difusión viscosa que perdura hasta alcanzar el estado de régimen; cuando todo el fluido alcanza la misma velocidad angular y por lo tanto la distribución de vorticidad es constante.
Si repitiéramos exactamente el mismo experimento pero con fluidos menos viscosos notaríamos un tiempo de transición más largo, mientras que para fluidos más viscosos tiempos más cortos; lo cual es un indicador de que la viscosidad está relacionada con la velocidad de difusión de vorticidad. Este mismo mecanismo de generación de vorticidad es el responsable de la generación de las capas circundantes alrededor de los cuerpos sólidos. El proceso de formación de estas regiones es similar, aunque en ellas se puede encontrar gradientes de presiones que modifican su desarrollo.
El ejemplo anterior deja como primer concepto que la viscosidad es la capacidad que tienen las partículas para contagiar su vorticidad y que dependiendo de ella el fluido estará en mayor o menor medida dominado por la vorticidad. Sin embargo el campo de movimiento de un fluido también esta caracterizado por otros factores: la escala del sistema (su longitud característica), su velocidad característica, y su densidad. El efecto de escala es un indicador de que el tamaño de un cuerpo es uno de los parámetros determinantes del campo de movimiento. Si se cuenta con dos modelos de un mismo contorno sólido pero de diferente escala y se hace circular a través de ellos un mismo fluido a la misma velocidad la vorticidad no tendrá porque difundir igual en ambos casos, por lo que la forma y/o intensidad de las regiones vorticosas no serán necesariamente idénticas. Si se quiere tener movimientos similares se deberá hacer circular por el cuerpo más grande un fluido menos denso, o a menor velocidad, o de mayor viscosidad.
Un ejemplo sencillo sobre el efecto de escala es la circulación de fluido tangente a un plano sólido, donde se concluye que el desarrollo de la capa circundante depende de la longitud. La densidad, por su lado, es un factor que interviene dinámicamente, porque al variar la masa de una partícula fluida varia su respuesta ante las acciones que se ejercen sobre ella. Desde este punto de vista más amplio es evidente que el nivel de difusión de vorticidad está estrechamente ligado al número de Reynolds del fluido.
Con una expresión matemática muy simple el número de Reynolds permite distinguir y comparar el movimiento de los fluidos. Esto se debe a que reúne las características fundamentales del movimiento: la escala de espacio y tiempo, la masa y las acciones internas. En términos generales se puede decir que cuando este número disminuye los fenómenos asociados a la viscosidad ganan preponderancia, y por lo tanto se puede esperar regiones vorticosas más extensas. Por el contrario, cuando se incrementa, los fenómenos viscosos se debilitan en relación a los no viscosos, y por lo tanto es de esperar regiones vorticosas más compactas.
La vorticidad en fluidos no viscosos
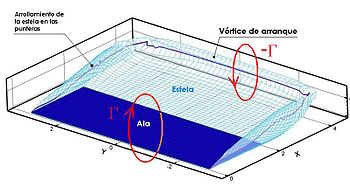
En los fluidos ideales (no viscosos e incompresibles) la vorticidad adquiere fundamental importancia. A pesar de que en ellos la ausencia de viscocidad impide la difusión de vorticidad, es posible encontrar regiones singulares extremadamente compactas donde la vorticidad es infinitamente intensa. Algunos ejemplos de estas regiones son los vórtices y las láminas vorticosas. Estas regiones singulares son empleadas en numerosos estudios de aerodinámica, como por ejemplo el de los perfiles alares Zhukovsky, y el método de Prandtl–Glauert.
La vorticidad y el campo de movimiento
Para fluidos estrictamente incompresibles, ya sean viscosos o no viscosos, existe una relación muy estrecha entre la vorticidad y el campo de movimiento definida por la ecuación integral de Tompson-Wu. Esta relación tiene un gran valor ya que permite evaluar el campo de movimiento a partir del campo de vorticidad, que es nulo en la mayor parte del dominio. La ecuación de Tomson-Wu aplicada a segmentos de vórtice en fluidos no viscosos adquiere la forma de la ecuación de Biot y Savart (Biot–Savart law). Estas dos ecuaciónes son empleadas en diversos métodos aerodinámicos como por ejemplo el "método inestacionario de la red de vórtices".
La vorticidad en la meteorología
En meteorología se habla de vorticidad para indicar la rotación del aire atmosférico. Se dice que la vorticidad es ciclónica (o positiva) cuando tiene sentido antihorario, y anticiclónica (o negativa) cuando tiene sentido horario (lo cual se verifica en el hemisferio norte).
La vorticidad es un campo muy útil para el pronóstico del tiempo pues está asociada a la producción de nubosidad: los campos de vorticidad positiva son nubosos mientras que los de vorticidad negativa estan asociados a cielos despejados. Esto se debe a que la vorticidad positiva está asociada con zonas de baja presión mientras que la negativa con zonas de alta presión. Por regla general, la alta presión produce divergencia del aire y cielos despejados, mientras que la baja presión produce convergencia y ascenso de aire lo que se resume en nubosidad.
Véase también
- Sustentación
- Circulación
- Capa límite
- Helmholtz
- Viscosidad
- Rotacional
- Principio de Bernoulli
- Reynolds
- Lord Kelvin
- Estela (rastro)
Enlaces externos
Categorías:- Magnitudes meteorológicas, climatológicas y atmosféricas
- Aerodinámica
Wikimedia foundation. 2010.