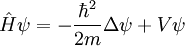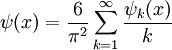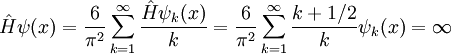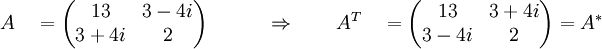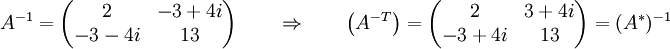Operador hermitiano

Operador hermitiano

Operador hermitiano

Un operador hermítico definido sobre un espacio de Hilbert es un operador lineal que, sobre un cierto dominio, coincide con su propio operador adjunto. Una propiedad importante de estos operadores es que sus autovalores son siempre números reales.

Cuando el dominio de un operador hermítico y el de su operador adjunto coinciden totalmente se dice entonces que es un operador autoadjunto. En un espacio de Hilbert de dimensión finita todo operador hermítico es además autoadjunto.

Contenido

Dimensión finita

En espacios de Hilbert de dimensión finita todo operador hermítico es además autoadjunto. Además en dimensión finita un operador hermítico fijada una base ortogonal viene dado por una matriz hermítica y diagonalizable.

Una matriz es hermítica o autoadjunta cuando es igual a su propia adjunta y es antihermítica cuando es igual a su traspuesta conjugada multiplicada por -1.

Sobre espacios vectoriales reales, las matrices hermíticas coinciden con las matrices simétricas y las antihermíticas con las antisimétricas. Estos operadores se pueden representar como una matriz diagonal (en una base ortonormal) de números reales. Este concepto se puede generalizar a un espacio de Hilbert de dimensión arbitraria.

Dimensión infinita

En espacios de dimensión infinita, como los espacios de Hilbert que aparecen en análisis funcional y en mecánica cuántica, un operador puede ser hermítico pero no autoadjunto (aunque todos los operadores autoadjuntos son evidentemente hermíticos).

El interés en los operadores en mecánica cuántica se debe a que en la formulación de Dirac-von Neumann, los posibles valores de los observables físicos o magnitudes físicas, son precisamente los autovalores de ciertos operadores que representan la magnitud física. Así pues el que un operador pueda ser interpretado como una magnitud físicamente medible requiere que sus autovalores sean números reales, condición que queda garantizada si los observables se representan por operadores hermíticos.

Operadores autoadjuntos

La consecuencia más importante de que un operador hermítico sea además autoadjunto es que entonces se le puede aplicar el teorema de descomposición espectral. Para un operador hermítico en un espacio de Hilbert de dimensión infinita en general no existe la "resolución espectral de la identidad", que sí está garantizada para operadores autoadjuntos.

Todos los operadores importantes de la mecánica cuántica como la posición, el momentum, el momento angular, la energía o el espín se representan como operadores autoadjuntos en un dominio denso espacio de Hilbert 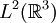L^2(\mathbb{R}^3). Otro operador particularmente importante para un sistema cuántico es el operador hamiltoniano definido por:

\hat{H} \psi = - \frac{\hbar^2}{2 m} \Delta \psi + V \psi


que, como observable, corresponde a la energía total de una partícula de masa m en un campo de potencial V y que para la mayoría de los sistemas es un operador no-acotado, relacionado con el hecho de que en esos sistemas no existe un valor máximo para la energía que puede tener una partícula.

Es interesante notar que normalmente los operadores no acotados, como el operador Hamiltoniano no están definidos en todo el espacio, sino solamente en un dominio denso. Los estados sobre los que no está definidos corresponderían a estados de "energía infinita". Por ejemplo para el oscilador armónico cuántico unidimensional en que V(x) = x2, el operador hamiltoniano no está definido sobre el estado cuántico:

\psi(x) = \frac{6}{\pi^2} \sum_{k=1}^\infty \frac{\psi_k(x)}{k}


Donde ψn(x) son los estados estacionarios normalizados, siendo la energía de cada uno de ellos \hat{H}\psi_n(x) = \hbar\omega[n+(1/2)]\cdot\psi_n(x). Es sencillo ver que el hamiltoniano no está definido para ese estado:

\hat{H}\psi(x) = \frac{6}{\pi^2} \sum_{k=1}^\infty \frac{\hat{H}\psi_k(x)}{k} = \frac{6}{\pi^2} \sum_{k=1}^\infty \frac{k+1/2}{k}\psi_k(x) = \infty


Ejemplos

Operador hermítico en dimensión finita

Matriz hermítica A+ := (A*)T= A. Los elementos de la diagonal deben ser reales, por ejemplo:

A \quad = \begin{pmatrix} 13 & 3-4i \\ 3+4i & 2 \end{pmatrix} \quad \qquad \Rightarrow \qquad A^T \quad = \begin{pmatrix} 13 & 3+4i \\ 3-4i & 2 \end{pmatrix} = A^*


Es interesante notar que la matriz inversa de una matriz hermítica es también hermítica:

A^{-1} = \begin{pmatrix} 2 & -3+4i \\ -3-4i & 13 \end{pmatrix}\qquad \Rightarrow \qquad \left(A^{-T}\right)= \begin{pmatrix} 2 & 3+4i \\ -3+4i & 13 \end{pmatrix} = (A^*)^{-1}



Operadores hermíticos en dimensión infinita

Véase también

Obtenido de "Operador hermitiano"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Operador hermítico — Un operador hermítico (tambien llamado hermitiano) definido sobre un espacio de Hilbert es un operador lineal que, sobre un cierto dominio, coincide con su propio operador adjunto. Una propiedad importante de estos operadores es que sus… …   Wikipedia Español

  • Hamiltoniano molecular — Este artículo o sección necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 14 de septiembre de 2011. También puedes ayudar… …   Wikipedia Español

  • Interpretación de Bohm — La interpretación de Bohm (también llamada teoría de la onda piloto o interpretación causal) es una interpretación de la teoría cuántica postulada por David Bohm en 1952 como una extensión de la onda guía de Louis de Broglie de 1927.… …   Wikipedia Español

  • Espacio de Hilbert — Saltar a navegación, búsqueda En matemáticas, el concepto de espacio de Hilbert es una generalización del concepto de espacio euclídeo. Esta generalización permite que nociones y técnicas algebraicas y geométricas aplicables a espacios de… …   Wikipedia Español

  • Matriz unitaria — En matemática, una matriz unitaria es una matriz compleja U, de n por n elementos, que satisface la condición: donde es la matriz identidad y es el traspuesto conjugado (también llamado el hermitiano adjunto o la hermítica) de U. Esta condición… …   Wikipedia Español

  • Superposición cuántica — es la aplicación del principio de superposición a la mecánica cuántica. Ocurre cuando un objeto posee simultáneamente dos o más valores de una cantidad observable (e.g. la posición o la energía de una partícula). Más específicamente, en mecánica… …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”