Oscilador armónico cuántico

Oscilador armónico cuántico

El oscilador armónico cuántico es el análogo mecánino cuántico del oscilador armónico clásico. Es uno de los sistemas modelo más importante en mecánica cuántica, ya que cualquier potencial se puede aproximar por un potencial armónico en las proximidades del punto de equilibrio estable (mínimo). Además, es uno de los sistemas mecánino cuánticos que admite una solución analítica sencilla.

Oscilador armónico monodimensional

Hamiltoniano, energía y autofunciones

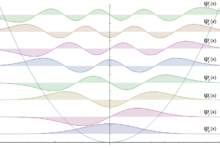
Funciones de onda para los ocho primeros autoestados, v = 0 a 7. El eje horizontal muestra la posición y en unidades (h/2πmω)1/2. Las gráficas están sin normalizar.
Densidades de probabilidad de los primeros autoestados (dimensión vertical, con los de menor energía en la parte inferior) para las diferentes localizaciones espaciales (dimensión horizontal).

En el problema del oscilador armónico unidimensional, una partícula de masa \displaystyle m está sometida a un potencial cuadrático \displaystyle V(x) = \frac{1}{2} k x^2. En Mecánica Clásica \displaystyle k= m \omega^2 se denomina constante de fuerza o constante elástica, y depende de la masa m de la partícula y de la frecuencia angular \displaystyle \omega.

El Hamiltoniano cuántico de la partícula es:

\hat H = \frac{\hat p^2}{2m} + \frac{1}{2} m \omega^2 x^2

donde x\, es el operador posición y \hat p\, es el operador momento \left(\hat p = -i \hbar {d \over dx} \right). El primer término representa la energía cinética de la partícula, mientras que el segundo representa su energía potencial. Con el fin de obtener los estados estacionarios (es decir, las autofunciones y los autovalores del Hamiltoniano o valores de los niveles de energía permitidos), tenemos que resolver la ecuación de Schrödinger independiente del tiempo

\hat H \left| \psi \right\rangle = E \left| \psi \right\rangle .

Se puede resolver la ecuación diferencial en la representación de coordenadas utilizando el método de desarrollar la solución en serie de potencias. Se obtiene así que la familia de soluciones es

\left\langle x | \psi_v \right\rangle = \sqrt{\frac{1}{2^v\,v!}} \cdot \left(\frac{m\omega}{\pi \hbar}\right)^{1/4} \cdot \exp \left(- \frac{m\omega x^2}{2 \hbar} \right) \cdot H_v\left(\sqrt{\frac{m\omega}{\hbar}} x \right)

v = 0, 1, 2, \ldots

donde v\, representa el número cuántico vibracional. Las ocho primeras soluciones (v = 0 \mbox{ a } 7\,) se muestran en la figura de la derecha. Las funciones Hn son los polinomios de Hermite:

H_n(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}e^{-x^2}

No se deben de confundir con el Hamiltoniano, que a veces se denota por H (aunque es preferible utilizar la notación \hat H para evitar confusiones). Los niveles de energía son

E_v = \hbar \omega \left(v + {1\over 2}\right) \qquad v = 0, 1, 2, \ldots .

Este espectro de energía destaca por tres razones. La primera es que las energías están "cuantizadas" y solamente pueden tomar valores discretos, en fracciones semienteras 1/2, 3/2, 5/2, ... de \hbar\omega. Este resultado es característico de los sistemas mecano-cuánticos. En la siguiente sección sobre los operadores escalera haremos un detallado análisis de este fenómeno. La segunda es que la energía más baja no coincide con el mínimo del potencial (cero en este caso). Así, la energía más baja posible es \hbar\omega/2, y se denomina "energía del estado fundamental" o energía del punto cero. La última razón es que los niveles de energía están equiespaciados, al contrario que en el modelo de Bohr o la partícula en una caja.

Conviene destacar que la densidad de probabilidad del estado fundamental se concentra en el origen. Es decir, la partícula pasa más tiempo en el mínimo del potencial, como sería de esperar en un estado de poca energía. A medida que la energía aumenta, la densidad de probabilidad se concentra en los "puntos de retorno clásicos", donde la energía de los estados coincide con la energía potencial. Este resultado es consistente con el del oscilador armónico clásico, para el cual la partícula pasa más tiempo (y por tanto es donde es más probable encontrarla) en los puntos de retorno. Se satisface así el principio de correspondencia.

Aplicación: moléculas diatómicas

Artículo principal: molécula diatómica

Para estudiar el movimiento de vibración de los núcleos se puede utilizar, en una primera aproximación, el modelo del oscilador armónico. Si consideramos pequeñas vibraciones en torno al punto de equilibrio, podemos desarrollar el potencial electrónico en serie de potencias. Así, en el caso de pequeñas oscilaciones el término que domina es el cuadrático, es decir, un potencial de tipo armónico. Por tanto, en moléculas diatómicas, la frecuencia fundamental de vibración vendrá dada por: [1]

\nu = \frac{1}{2\pi} \sqrt{\frac{k}{\mu}}

que se relaciona con la frecuencia angular mediante \omega = 2 \pi \nu \, y depende de la masa reducida \mu \, de la molécula diatómica.


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Oscilador armónico — Se dice que un sistema cualquiera, mecánico, eléctrico, neumático, etc. es un oscilador armónico si cuando se deja en libertad, fuera de su posición de equilibrio, vuelve hacia ella describiendo oscilaciones sinusoidales, o sinusoidales… …   Wikipedia Español

  • Estado cuántico — Saltar a navegación, búsqueda El estado cuántico es la descripción del estado físico de un sistema cuántico. Son los valores especificos de las propiedades observables físicas cuantificables que caracterizan el sistema cuántico definido. La… …   Wikipedia Español

  • Hilo cuántico — En física de la materia condensada, un hilo cuántico es un alambre conductor eléctrico en el que los efectos cuánticos afectan las propiedades del transporte. Debido al confinamiento de electrones de conducción en la dirección transversal del… …   Wikipedia Español

  • Teorema de equipartición — Figura 1. Movimiento térmico de un péptido tipo hélice α. El movimiento vibratorio es aleatorio y complejo, y la energía de un átomo en particular puede fluctuar ampliamente. Sin embargo, el teorema de equipartición permite que se pueda calcular… …   Wikipedia Español

  • Operador escalera — En álgebra lineal, Analisis funcional y en sus aplicaciones a la mecánica cuántica, un operador de subida o de bajada (también conocidos como operadores escalera) es un operador que aumenta o disminuye el autovalor de otro operador. En mecánica… …   Wikipedia Español

  • Teoría cuántica de campos — Dispersión de neutrones. La dispersión inelástica de …   Wikipedia Español

  • Hamiltoniano (mecánica cuántica) — El Hamiltoniano H tiene dos significados distintos, aunque relacionados. En mecánica clásica, es una función que describe el estado de un sistema mecánico en términos de variables posición y momento, y es la base para la reformulación de la… …   Wikipedia Español

  • Límite de Lamb Dicke — En los experimentos con iones atrapados existe una región cuántica llamada el límite de Lamb Dicke. En esta región el acoplamiento (inducido por un campo electromagnético externo) entre los estados electrónicos internos (los estados del qubit) y… …   Wikipedia Español

  • Energía del punto cero — Saltar a navegación, búsqueda En física, la energía del punto cero es la energía más baja que un sistema físico mecánico cuántico puede poseer, y es la energía del estado fundamental del sistema. El concepto de la energía del punto cero fue… …   Wikipedia Español

  • Wikiproyecto:Revisión por pares — Uno de nuestros revisores ganándose el pan. Atajo …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”