Función Z

Función Z

En matemática, la función Z es una función usada para el estudio de la función zeta de Riemann a lo largo de la recta crítica, donde la parte real del argumento es 1/2. Es también llamada función Z de Riemann-Siegel o función zeta de Hardy.[1] Ésta puede ser definida en términos de la función theta de Riemann-Siegel y de la función zeta de Riemann como:[1]

Z(t) = e^{i \theta(t)} \zeta\left(\frac{1}{2}+it\right).

Contenido

Propiedades

Se puede deducir de la ecuación funcional de la función zeta de Riemann que la función Z es real para valores reales de t. Es una función impar, y analítica para valores del argumento reales. De hecho, se puede observar que la función theta de Riemann-Siegel y la función zeta de Riemann son ambas holomorfas en la recta crítica, y donde la parte imaginaria de t está comprendida entre -1/2 y 1/2, la función Z es holomorfa en el rango crítico también.[2] Más aun, los ceros reales de Z(t) son precisamente los ceros de la función zeta a lo largo de la recta crítica, y los ceros complejos de la función Z dentro del rango crítico, corresponden a los ceros complejos fuera de la recta crítica de la función zeta de Riemann.


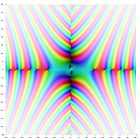
Función theta de Riemann-Siegel en el plano complejo
Riemann Siegel Z 1.jpg
Riemann Siegel Z 2.jpg
-5 < \Re(t) < 5 -40 < \Re(t) < 40

Véase también

Referencias

  1. ↑ a b Weisstein, Eric W. (2005). «Riemann-Siegel Functions» (en inglés). Consultado el 15 de enero de 2010.
  2. ↑ Berry, M. V. (1995). «The Riemann-Siegel Expansion for the Zeta Function: High Orders and Remainders». The royal society 450 (1939). p. 439-462. http://rspa.royalsocietypublishing.org/content/450/1939/439.abstract. 

Bibliografía

  • Edwards, H. M., Riemann's Zeta-Function, Academic Press, 1974
  • Paris, R. B., and Kaminski, D., Asymptotics and Mellin-Barnes Integrals, Cambridge University Press, 2001
  • Ramachandra, K., On the Mean-Value and Omega-Theorems for the Riemann Zeta-Function, Springer-Verlag, 1995
  • Edward Charles Titchmarsh, The Theory of the Riemann Zeta-Function, second revised (Heath-Brown) edition, Oxford University Press, 1986

Enlaces externos

  • Wolfram Research (2009). «RiemannSiegelZ» (en inglés). Consultado el 15 de enero de 2010.

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • función — (Del lat. functĭo, ōnis). 1. f. Capacidad de actuar propia de los seres vivos y de sus órganos, y de las máquinas o instrumentos. 2. Tarea que corresponde realizar a una institución o entidad, o a sus órganos o personas. 3. Acto solemne,… …   Diccionario de la lengua española

  • función — sustantivo femenino 1. Actividad o acción propias de una persona o de una cosa: la función de la sangre en el organismo, la función de la policía en la sociedad. La función de este pedal es activar el freno. 2. (preferentemente en plural)… …   Diccionario Salamanca de la Lengua Española

  • función — en función de. Locución preposicional que significa ‘según o dependiendo de’: «No amaré a los demás en función de sus aciertos o errores» (Cuauhtémoc Grito [Méx. 1992]). Cuando va seguida de una subordinada sustantiva introducida por que, debe… …   Diccionario panhispánico de dudas

  • función — acción característica o especial de un órgano una parte o aparato. Diccionario ilustrado de Términos Médicos.. Alvaro Galiano. 2010. función Acto, proceso o serie de procesos que sirven a un …   Diccionario médico

  • Función — (Del lat. functio, onis.) ► sustantivo femenino 1 BIOLOGÍA Actividad o capacidad de acción específica de un ser vivo y de sus órganos: ■ la función del riñón; la función clorofílica. 2 Desempeño de un cargo u oficio: ■ el vicepresidente desempeña …   Enciclopedia Universal

  • Función — El término función puede referirse a: Función matemática, una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el codominio) de forma que a cada elemento del dominio le corresponde un único elemento del codominio.… …   Wikipedia Español

  • función — {{＃}}{{LM F18444}}{{〓}} {{SynF18925}} {{［}}función{{］}} ‹fun·ción› {{《}}▍ s.f.{{》}} {{＜}}1{{＞}} Acción o actividad propias de algo o del cargo o la profesión que se tienen: • La función de las pestañas es impedir que entren partículas extrañas en …   Diccionario de uso del español actual con sinónimos y antónimos

  • función — s f 1 Acción, actividad u oficio que cumple, desempeña o es propio de algo o alguien: las funciones del organismo, la función del alimento, Tiene una función didáctica 2 (Mat) Regla por la cual a cada valor de un conjunto corresponde exactamente… …   Español en México

  • función — (f) (Básico) actividad particular de una cosa, persona u organismo Ejemplos: La escuela cumple una función pedagógica e informativa. La principal función de los riñones es la de eliminar las toxinas del organismo …   Español Extremo Basic and Intermediate

  • Función L — La teoría de las funciones L se ha convertido en una parte muy substancial, y todavía con numerosas conjeturas, de la teoría de números contemporánea. En ella, se construyen amplias generalizaciones de la función zeta de Riemann y de las series L …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”