Axioma de unión

Axioma de unión

Axioma de unión

El axioma de unión, uno de los axiomas de la teoría de Zermelo-Fraenkel, establece que, dada cualquier colección (conjunto) de conjuntos C, existe un conjunto, representado por 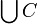\bigcup C y llamado unión de C, que contiene todos los elementos de cada conjunto de C. Esto es,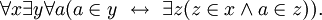

\forall x\exists y\forall a (a\in y\ \leftrightarrow\ \exists z(z\in x\wedge a\in z)).

Consecuencias del axioma de pares en ZF

Si A es una colección de conjuntos, entonces la unión 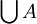\bigcup A contiene aquellos y solo aquellos elementos que están en algún conjunto de A. Si 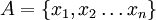A=\{x_1,x_2\ldots x_n\}, un conjunto con n elementos, entonces es común escribir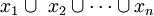

x_1\cup\ x_2\cup\cdots\cup x_n

para representar la unión de los conjuntos de A. Es fácil ver que

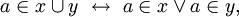
a\in x\cup y\ \leftrightarrow\ a\in x\vee a\in y ,

de modo que el axioma de unión y el axioma de pares garantizan la existencia del conjunto 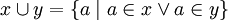x\cup y=\{a\mid a\in x\vee a\in y\} para cualesquiera conjuntos x e y, un hecho que no puede deducirse simplemente del esquema de especificación junto con los axiomas restantes. A diferencia de la unión, la intersección de conjuntos es deducible a partir del axioma de pares y el esquema de especificación. Efectivamente, pues se define el conjunto 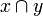x\cap y mediante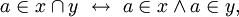

a\in x\cap y\ \leftrightarrow\ a\in x\wedge a\in y,

y por tanto 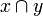x\cap y existe. Más general, se define el conjunto

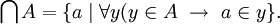\bigcap A=\{a\mid \forall y(y\in A\ \rightarrow\ a\in y\}.
Obtenido de "Axioma de uni%C3%B3n"

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Unión de conjuntos — La unión de los conjuntos A y B es otro conjunto A ∪ B que contiene todos los elementos de A y de B. En la teoría de conjuntos, la unión de dos (o más) conjuntos es una operación que resulta en otro conjunto cuyos elementos son los elementos de… …   Wikipedia Español

  • Axioma de elección — Saltar a navegación, búsqueda En matemáticas, el axioma de elección o axioma de escogencia, abreviado usualmente AE, o AC por sus siglas en inglés, es un axioma de la teoría de conjuntos. Intuitivamente, AE dice que dada una colección de… …   Wikipedia Español

  • Axiomas de Zermelo-Fraenkel — Los axiomas de Zermelo Fraenkel, formulados por Ernst Zermelo y Adolf Fraenkel, son un sistema axiomático concebido para formular la teoría de conjuntos. Normalmente se abrevian como ZF o en su forma más común, complementados por el axioma de… …   Wikipedia Español

  • Anarcocapitalismo — Saltar a navegación, búsqueda Bandera aurinegra, símbolo del anarcocapitalismo, el amarillo representa la moneda fuerte (o la propiedad privada) y el negro representa el anarquismo.[1 …   Wikipedia Español

  • Teoría de haces — En matemática, un haz F sobre un espacio topológico dado, X, proporciona, para cada conjunto abierto U de X, un conjunto F(U), de estructura más rica. A su vez dichas estructuras: F(U), son compatibles con la operación de restricción desde un… …   Wikipedia Español

  • Número cardinal (teoría de conjuntos) — Este artículo trata sobre números cardinales en teoría de conjuntos axiomática. Para una introducción más básica, véase Número cardinal. Comparación de los cardinales numerable y continuo. Cada sucesión binaria, compuesta por una cantidad… …   Wikipedia Español

  • WALL·E — Título WALL·E …   Wikipedia Español

  • Accesibilidad — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Espacio de Baire — Saltar a navegación, búsqueda En topología y ramas relacionadas de las matemáticas, un espacio de Baire es un espacio topológico que, hablando intuitivamente es muy grande y tiene suficientes puntos para un cierto proceso límite. Fue nombrado así …   Wikipedia Español

  • CW-complejo — Saltar a navegación, búsqueda En Topología y Geometría, un complejo celular o CW Complejo es un tipo de espacio topológico que en cierta manera se asemeja a una variedad topológica. Son espacios muy utilizados en Topología (especialmente en… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”