Número cardinal (teoría de conjuntos)

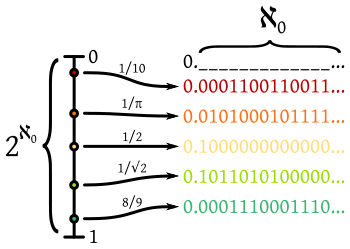Este artículo trata sobre números cardinales en teoría de conjuntos axiomática. Para una introducción más básica, véase Número cardinal.

Comparación de los cardinales numerable y continuo. Cada sucesión binaria, compuesta por una cantidad numerable de "decimales binarios", corresponde a un punto del segmento entre 0 y 1. El "número" de decimales en cada sucesión es ℵ₀. El "número" de puntos en el segmento es 2^ℵ₀: dos posibilidades (0 ó 1) para cada decimal de cada sucesión.

En teoría de conjuntos, un número cardinal o cardinal es una generalización de los números naturales para contar el número de elementos, la cardinalidad, de cualquier conjunto, finito o infinito. El cardinal de un conjunto finito es un número natural ordinario. El cardinal de un conjunto infinito es un número transfinito. Los cardinales clasifican los conjuntos de manera más "tosca" que los números ordinales, que distinguen no sólo el número de elementos de un conjunto sino también la manera en la que están ordenados.

Los cardinales se definen mediante la noción de "equipotencia", que relaciona dos conjuntos si tiene "el mismo número de elementos". Establecida esta relación, los cardinales son representantes de todos los tamaños posibles para un conjunto. Puede demostrarse que existen conjuntos infinitos con distinto tamaño. Por ejemplo, los conjuntos de los números naturales y de los números reales no tienen el mismo cardinal. De hecho es necesaria una colección infinita de números transfinitos para clasificar todos los conjuntos infinitos.

Existe una sucesión infinita de cardinales:

$0,\,1,\,2,\,3,\,\ldots,\,\aleph_0,\,\aleph_1,\,\aleph_2,\,\ldots,\,\aleph_\omega,\ldots$

que empieza con los números naturales (con cero), y continúa con los números alef, que son cardinales de conjuntos bien ordenados. Cada alef tiene un índice, un cierto número ordinal, que indica su posición dentro de la serie. Dependiendo de si se asume el axioma de elección o no, los alefs agotan todos los cardinales posibles o no.

Introducción histórica

En 1874, Georg Cantor probó que no todos los conjuntos infinitos tienen la misma "potencia", sino que al menos existían dos tipos: los "enumerables", como los números naturales y los "no enumerables", como los puntos de una recta.

En su obra Fundamentos para una teoría general de conjuntos, Cantor introdujo la noción de número transfinito, como una generalización de los números naturales, que va más allá de ellos formando una serie ordenada e ilimitada:

$0,\,1,\,2,\,\ldots\,,\,\omega,\,\omega+1,\,\omega+2,\,\ldots\,,\,\omega\cdot2,\,\omega\cdot2+1,\,\ldots\,,\,\omega\cdot3,\,\dots\,,\,\omega\cdot n,\,\ldots\,,\,\omega\cdot\omega=\omega^2,\,\ldots\,,\,\omega^3,\,\ldots\,,\,\omega^n,\,\ldots\,,\,\omega^\omega,\,\ldots\,,$

Cantor descubrió que cada número transfinito se correspondía con un número ordinal, que representa la posición de un elemento en un cierto conjunto bien ordenado, y también que los transfinitos se organizaban en clases numéricas.

Así, clasificaba a los números naturales en la clase numérica (I), que es mayor que todos ellos. Los números de la clase numérica (II) son todos los que tengan la misma "potencia" que la clase numérica (I), esto es, que sean numerables (todos los transfinitos mostrados arriba son de esa clase), etc. Introduciendo la notación ℵ_n para hablar de la clase numérica (n + 1), demostró que en la serie transfinita se dan infinitas clases numéricas cada vez más grandes.

Estas clases numéricas formaban pues otra serie transfinita, pero no de números ordinales, sino de números cardinales, que clasifican todas las posibles potencias de un conjunto infinito.

Equipotencia

El concepto de cardinalidad depende de forma crucial del concepto de equipotencia. Incluso si no se pueden "contar" los elementos de un conjunto infinito, sí puede afirmarse si dos conjuntos "tienen el mismo número de elementos" o no. Para ello, ha de establecerse si existe una relación biunívoca entre los elementos de ambos.

Una relación biunívoca entre dos conjuntos A y B es un criterio por el cual se empareja cada elemento de A con un elemento de B, de forma que todos los elementos de B sean pareja de un elemento de A y sólo de uno.

Ejemplo

Sean los conjuntos de números:

N = {1, 2, 3, 4, 5, 6, ...} (los números naturales sin cero)
P = {2, 4, 6, 8, 10, 12, ...} (los números pares)

Es obvio que el segundo conjunto es un subconjunto del primero, P ⊂ N. Sin embargo, aunque intuitivamente esto parezca significar que P es "más pequeño" que N, lo cierto es que son equipotentes, puesto que siempre se puede emparejar un número par con su mitad, n ↔ n/2. De este modo:

{2 ↔ 1, 4 ↔ 2, 6 ↔ 3, 8 ↔ 4, 10 ↔ 5, 12 ↔ 6, ...}

Es claro que cada número par tiene una "pareja" única, y que todo número natural p es la pareja de algún número par (a saber, 2p).

De esta manera se define "tener el mismo cardinal":

Dos conjuntos A y B se dicen equipotentes (o con el mismo cardinal, la misma cardinalidad, el mismo número de elementos, la misma potencia, etc.) si existe una función biyectiva f : A → B entre ellos.

La relación de equipotencia es entonces una relación de equivalencia, que captura la noción de "tener el mismo cardinal", incluso antes de tener una definición de qué es un número cardinal. Es decir, se denota:

$|A|=|B|\Leftrightarrow\ A\text{ y }B\ \text{son equipotentes ,}$

incluso cuando el símbolo |A| por sí solo no está definido. Esta idea se ve reforzada adoptando la siguiente definición:

$|A|\leq|B|\Leftrightarrow\text{ Existe }f:A\to B\text{ inyectiva ,}$

es decir, la potencia de un conjunto A es menor o igual que la de otro B si se puede emparejar cada elemento de A con algún elemento de B sin repetir ninguna pareja en B (pero no necesariamente todo elemento de B es pareja de algún elemento de A). Entonces puede demostrarse que la relación de "tener menos cardinal que" tiene las propiedades intuitivas que debe: |A| ≤ |B| y |B| ≤ |C| implican que |A| ≤ |C|; y |A| ≤ |B| más |B| ≤ |A| implica que |A| = |B| (esto último constituye el teorema de Cantor-Bernstein-Schröder). Es decir, la relación de minuspotencia es una relación de orden.

Definición formal

La definición formal de número cardinal escoge un representante canónico de cada cardinalidad. Por ejemplo, la construcción usual de los números naturales en teoría de conjuntos los define como unos conjuntos concretos:

0 ≡ ∅, 1 ≡ {0}, 2 ≡ {0, 1}, ...

De este modo, "el cardinal de X = {a, b} es 2" es equivalente a decir "X y {0, 1} son equipotentes". Al definir número cardinal de manera general se extiende este razonamiento a cualquier conjunto, finito o infinito.

Al definir número cardinal se construye una asignación en la que a cada conjunto X le corresponde otro conjunto card(X) (único), de forma que se cumplan la siguiente propiedad básica:

$\text{card}(X)=\text{card}(Y)\Leftrightarrow |X|=|Y|$

De este modo, la igualdad |X| = |Y| no es sólo notación, sino que los símbolos a izquierda y derecha tienen un significado independiente. Al cardinal de un conjunto X se le denota entonces por $\displaystyle \bar{\bar X}\,\!$ , card(X), |X| o #X.^[1]

Existen diversas formas de construir esta asignación, dependiendo de los axiomas que se asuman para la teoría de conjuntos.

Cardinales de Von Neumann

La definición de cardinal para un conjunto bien ordenable es muy simple. Un conjunto bien ordenable es isomorfo bajo orden (y equipotente en particular) a algún ordinal. Sin embargo, en general, dos ordinales infinitos distintos pueden ser equipotentes: por ejemplo, todos los ordinales de la forma ω·n + m con m y n ≥ 1 naturales son numerables, esto es, equipotentes a los números naturales ω. Sin embargo, es muy sencillo escoger un único ordinal de entre todos los que son equipotentes entre sí:

Los cardinales de Von Neumann κ son aquellos ordinales no equipotentes a ninguno de sus anteriores:

$\forall\alpha<\kappa\,,\,|\alpha|\neq|\kappa|$ ,

es decir, un cardinal de Von Neumann es un ordinal inicial, el primer ordinal de cada "clase numérica" de Cantor. Se tiene entonces que:

Todo conjunto bien ordenable es equipotente a un único cardinal de Von Neumann.

Dos conjuntos bien ordenables son equipotentes si y sólo si les corresponde el mismo cardinal.

Los cardinales de Von Neumann se suelen denotar por letras griegas de entre la mitad del alfabeto: κ, μ, ν, etc.

De este modo, un ordinal cualquiera $α$ está comprendido entre dos cardinales de Von Neumann, y al mayor de ellos se le llama cardinal siguiente a $α$ , $α$ ⁺. Asumiendo el axioma de elección como cierto, entonces todo conjunto es bien ordenable y equipotente a un único cardinal de Von Neumann.

La función alef

Artículo principal: Función alef

La serie de los alefs asigna un cardinal de Von Neumann infinito ℵ_$α$ a cada ordinal $α$ mediante recursión transfinita:

El alef asociado a un ordinal viene dado por:

$\aleph_0=\omega\text{ , }\aleph_{\alpha+1}=\aleph_\alpha^+\text{ , }\aleph_\lambda=\bigcup_{\alpha<\lambda}\aleph_\alpha$

y por esto se denota habitualmente al cardinal de los números naturales como ℵ₀. Puede demostrarse que todo cardinal de Von Neumann infinito es un alef.

Definición general

El axioma de elección es independiente del resto de axiomas de la teoría de conjuntos. Por tanto, si no se asume (o se postula su negación), no todo conjunto es bien ordenable, ni equipotente a un cardinal de Von Neumann. Sin embargo, es posible definir una noción distinta y más general de número cardinal que se extienda para todos los conjuntos.

La idea original para escoger un representante de cada cardinalidad de manera única era definir un cardinal como una clase de equivalencia de todos los conjuntos equipotentes a uno dado. Esta noción sencilla, que prevaleció en la literatura hasta los años 50, es inapropiada dado que esta clase de equivalencia no es un conjunto. Sin embargo, recurriendo al concepto de rango, puede demostrarse que la colección de todos los conjuntos equipotentes a uno dado de rango mínimo es un conjunto. Mediante esta herramienta —debida originalmente a Dana Scott— se puede definir número cardinal en general:^[2]

Un cardinal $\mathfrak p$ es un conjunto que verifica:

Todos sus elementos son equipotentes entre sí.

Todos sus elementos tienen el mismo rango.

No existen conjuntos equipotentes a los elementos de $\mathfrak p$ de rango menor al rango común de estos.

Cualquier conjunto equipotente a los elementos de $\mathfrak p$ y con el mismo rango es un elemento de $\mathfrak p$ .

Los número cardinales así definidos (generales) se suelen denotar por letras góticas: $\mathfrak p$ , $\mathfrak q$ , etc. De esta definición se puede demostrar la generalización del teorema anterior:

Todo conjunto es equipotente a los elementos de un único cardinal (su cardinal).

Dos conjuntos son equipotentes si y sólo si tienen el mismo cardinal.

Diferencias

En general, los cardinales de Von Neumman son un subconjunto de la totalidad de los cardinales generales,^[3] que en particular contiene todos los cardinales finitos. Si se asume el axioma de elección, todo cardinal infinito es un alef, y además los cardinales están bien ordenados, en el sentido de que dados dos conjuntos, uno de ellos es biyectable con un subconjunto del otro. Puede demostrarse que estas propiedades son de hecho equivalentes al axioma de elección:

Son equivalentes:

El axioma de elección.

Todo cardinal infinito es un alef.

Ley de la tricotomía: dados dos conjuntos, uno de ellos es biyectable con un subconjunto del otro.

Además, los cardinales de Von Neumman "tienen el cardinal que representan": para todo κ, |κ| = κ. Los cardinales según la construcción general no tienen esta propiedad, y de hecho puede demostrarse que, en la teoría de Zermelo-Fraenkel sin el axioma de elección, no existe ninguna definición de cardinal que la tenga.

Aritmética cardinal

Es posible definir unas suma, multiplicación y exponenciación de cardinales, de forma similar al caso de la aritmética ordinal, aunque las propiedades de la primera son más parecidas a la aritmética ordinaria.

Suma

Dados dos conjuntos finitos y disjuntos, el número de elementos de su unión es la suma del número de elementos de ambos. En la suma de dos cardinales se generaliza esta idea, al demostrarse:

El cardinal de la unión de dos conjuntos disjuntos sólo depende del cardinal dichos conjuntos:

$|A|=|A'|\text{ , }|B|=|B'|\text{ y }|A\cap B|=|A'\cap B'|=\empty\Rightarrow |A\cup B|=|A'\cup B'|$

De este modo puede definirse:

$\mathfrak p+\mathfrak q=\text{card}\Big([A\times\{0\}]\cup[B\times\{1\}]\Big)\text{ , donde }\text{card}(B)=\mathfrak q\text{ y }\text{card}(A)=\mathfrak p$

En esta definición no se toma la unión de los dos cardinales directamente para evitar un posible solapamiento de sus elementos. De este modo se demuestra:

Dados dos conjuntos disjuntos generales X e Y, card(X ∪ Y) = card(X) + card(Y).
La suma cardinal es conmutativa —a diferencia de la aritmética ordinal—, asociativa y con elemento neutro ( $\mathfrak p+0=\mathfrak p$ , donde 0 ≡ ∅).
La suma de ordinales y de cardinales son compatibles: card( $α$ + $β$ )=card( $α$ ) + card( $β$ ), donde $α$ y $β$ son ordinales, y el signo "+" del miembro izquierdo se refiere a la suma de ordinales.

Ejemplo

Sean los conjuntos:

A = {♠, ◊}

B = {Δ, ♦, Z}

N = {0, 1, 2, 3, ...} (los números naturales)

Es obvio que card(A ∪ B) = card(A) + card(B) =2 + 3 = 5. Para calcular card(A ∪ N) se ha de observar que A ∪ N = {♠, ◊, 0, 1, 2, 3, ...} tiene el mismo número de elementos que N:

{♠ ↔ 0, ◊ ↔ 1, 0 ↔ 2, 1 ↔ 3, 2 ↔ 4, 3 ↔ 5, ...}

En otras palabras, card(N) + card(A) = ℵ₀ + 2 = ℵ₀. En general se tiene ℵ₀ + n = ℵ₀ para cualquier número natural n.

Producto

De igual modo, al tomar el producto cartesiano de dos conjuntos finitos, el número de los elementos de este producto es igual al producto del número de elementos de ambos conjuntos. De nuevo, se generaliza esta idea para definir el producto de dos cardinales, donde se demuestra:

El cardinal del producto cartesiano de dos conjuntos sólo depende del cardinal de dichos conjuntos:

$|A|=|A'|\text{ y }|B|=|B'|\Rightarrow |A\times B|=|A'\times B'|$

Y entonces se define:

$\mathfrak p\cdot\mathfrak q=\text{card}\left(A\times B\right)\text{ , donde }\text{card}(B)=\mathfrak q\text{ y }\text{card}(A)=\mathfrak p$

De este modo, se demuestra:

Dados dos conjuntos X e Y, card(X × Y) = card(X)·card(Y).
La multiplicación cardinal es conmutativa —a diferencia de la aritmética ordinal—, asociativa, distributiva respecto de la suma, con elemento neutro ( $\mathfrak p\cdot1=\mathfrak p$ , donde 1 ≡ {0}) y elemento absorbente ( $\mathfrak p\cdot0=0$ ).
El producto de ordinales y de cardinales son compatibles: card( $α$ · $β$ ) = card( $α$ )·card( $β$ ), donde $α$ y $β$ son ordinales, y el signo "·" del miembro izquierdo se refiere al producto de ordinales.

Ejemplo

Utilizando los mismos conjuntos del ejemplo anterior, el producto de A y B es:

A × B = {(♠,Δ), (♠,♦), (♠,Z), (◊,Δ), (◊,♦), (◊,Z)} y obviamente card(A × B) = card(A) × card(B) = 2 × 3 = 6. Para calcular card(A × N) se ha de observar que el conjunto:

A×N = {(♠,0), (◊,0), (♠,1), (◊,1), (♠,2), (◊,2), ...}

tiene el mismo número de elementos que N:

{(♠,0) ↔ 0, (◊,0) ↔ 1, (♠,1) ↔ 2, (◊,1) ↔ 3, (♠,2) ↔ 4, (◊,2) ↔ 5, ...}

de modo que en general (♠,n) ↔ 2n y (◊,n) ↔ 2n + 1. Así, card(A × N) = card(A) × card(N) = 2 × ℵ₀ = ℵ₀, y en general se tiene n × ℵ₀ = ℵ₀ para todo número natural no nulo.

Exponenciación

Por último, a la hora de tomar potencias de cardinales, se generaliza el hecho de que dados dos conjuntos finitos X e Y, existen exactamente #Y^#X funciones posibles cuyo dominio es X y cuyo codominio es Y. Denotando por B^A el conjunto de todas las aplicaciones f : A → B, se tiene la siguiente propiedad:

El cardinal del conjunto de funciones entre dos conjuntos sólo depende del cardinal de dichos conjuntos:

$|A|=|A'|\text{ y }|B|=|B'|\Rightarrow |B^A|=|B'^{A'}|$

Aprovechando esta propiedad puede definirse:

$\mathfrak q^{\mathfrak p}=\text{card}(B^A)\text{, donde }\text{card}(B)=\mathfrak q\text{ y }\text{card}(A)=\mathfrak p$

Con esta definición puede entonces demostrarse:

Dados dos conjuntos cualesquiera X e Y, card(Y^X) = card(Y)^card(X).
Varias propiedades básicas de la exponenciación de números se mantienen:

$\mathfrak p^{\mathfrak s}\mathfrak p^{\mathfrak t}=\mathfrak p^{\mathfrak s+\mathfrak t}\text{ , }\mathfrak p^{\mathfrak s}\mathfrak q^{\mathfrak s}=(\mathfrak p\cdot \mathfrak q)^{\mathfrak s}\text{ , }\mathfrak p^1=\mathfrak p\text{ , }\mathfrak p^0=1\text{ , }1^\mathfrak p=1\text{ , }0^\mathfrak p=0\text{ si }\mathfrak p\neq 0$ .
La exponenciación de ordinales y de cardinales no son compatibles. Por ejemplo, en la exponenciación ordinal se tiene 2^ω = ω. Sin embargo, card(2^ω) = card(ω) = ℵ₀ ≠ 2^card(ω) = 2^ℵ₀, donde la segunda exponenciación es cardinal.

Ejemplo

Utilizando los mismos conjuntos de los ejemplos anteriores, la potencia A^B es el conjunto de todas las funciones con dominio B y codominio A. Una función f : B → A viene especificada por las imágenes f(Δ), f(♦) y f(Z). Para los tres casos, estas imágenes pueden ser ♠ ó ◊, sin ninguna restricción, Por tanto, hay dos posibilidades para cada imagen y 3 imágenes a determinar, con lo que hay 2×2×2 posibilidades. Por tanto card(B^A) = card(B)^card(A) = 2³ = 8.

En el caso N^A, se han de encontrar todas las funciones f : A → N, especificando las imágenes f(♠) y f(◊), que pueden valer ambas cualquier número natural. Así, una función queda especificada por un par ordenado de números (m,n). Pero es conocido que hay tantos pares ordenados de números como números. Por tanto N^A es equipotente a N y card(N^A) = card(N)^card(A) = ℵ₀² = ℵ₀. En general, para todo número natural no nulo n, ℵ₀ⁿ = ℵ₀.

El caso A^N es distinto, pues se han de encontrar todas las funciones f : N → A, especificando las imágenes de cada número natural f(n), que pueden valer ♠ o ◊. Si se adopta el convenio de que ♠ significa SI y ◊ significa NO, puede entenderse que cada f equivale a un subconjunto de N: aquel que contiene sólo los elementos cuya imagen es SI. Es obvio pues que A^N es equipotente a la colección de todos los subconjuntos de N. Puede demostrarse que card(A^N) = 2^ℵ₀ es estrictamente mayor que ℵ₀, y que de hecho es el cardinal de los números reales.

Hipotesis del continuo

Artículo principal: Hipótesis del continuo

La hipótesis del continuo es la cuestión de la existencia o no existencia de un cardinal entre los números naturales y los números reales. El conjunto de los números reales es equipotente al conjunto de todos los conjuntos de números naturales, cuya potencia es c ≡ 2^ℵ₀.

Hipótesis del continuo

No existe un cardinal entre ℵ₀ y c.

Si se asume el axioma de elección, existe un mínimo cardinal mayor que ℵ₀, ℵ₁. La hipótesis del continuo puede formularse entonces como "c es igual a ℵ₁".

Puede demostrarse que en las teorías estándar de conjuntos, este enunciado es independiente: tanto él como su negación son compatibles con los axiomas de la teoría de conjuntos.

Referencias

↑ Para un ordinal $α$ su cardinal suele representarse por $\scriptstyle\bar\alpha$ . La notación original de Cantor usaba una barra, $\scriptstyle\bar X$ , para abstraer las propiedades de los elementos del conjunto X exceptuando su orden —representando su ordinal—, y dos barras $\scriptstyle \bar{\bar X}\,\!$ , para hacer la "doble abstracción" y quedarse sólo con la cantidad de elementos, su cardinal. En el caso de un ordinal pues, sólo es necesario añadir una barra para obtener el cardinal correspondiente.
↑ Véase Deiser, 2010.
↑ Estrictamente hablando, esto no es correcto: los cardinales de Von Neumman κ son unos ciertos ordinales y los cardinales generales no. "Subconjunto" ha de interpretarse en términos de la colección de todos los κ, donde la barra toma el cardinal general.

Cantor, Georg (2006) [1872-1899]. Fundamentos para una teoría general de conjuntos. Escritos y correspondencia selecta.. Edición de José Ferreirós. Crítica. ISBN 84-8432-695-0.
Deiser, Oliver (May 2010). «On the Development of the Notion of a Cardinal Number». History and Philosophy of Logic 31 (2). doi:10.1080/01445340903545904.
Ivorra, Carlos, Lógica y teoría de conjuntos, http://www.uv.es/ivorra/Libros/Logica.pdf, consultado el 18-10-2010 .
Jech, Thomas J. (1973) (en inglés). The Axiom of Choice. North-Holland. ISBN 0-7204-2275-2.
Rubin, Jean E. (1967) (en inglés). Set Theory for the Mathematician. Holden-Day. OCLC 816225.
Este artículo fue creado a partir de la traducción del artículo Cardinal number de la Wikipedia en inglés, bajo licencia Creative Commons Atribución Compartir Igual 3.0 y GFDL.

Categoría:

Teoría de conjuntos

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

Número ordinal (teoría de conjuntos) — Este artículo trata sobre números ordinales en teoría de conjuntos axiomática. Para una introducción más básica, véase Número ordinal. Representación del ordinal ωω. Cada vuelta alrededor de esta espiral representa una potencia entera de ω: la… … Wikipedia Español
Número cardinal — Este artículo trata sobre la definicón elemental de número cardinal. Para la definición en teoría de conjuntos, véase Número cardinal (teoría de conjuntos). El cardinal indica el número o cantidad de elementos de un conjunto, sea esta cantidad… … Wikipedia Español
Número natural — Los números naturales pueden usarse para contar (una manzana, dos manzanas, tres manzanas, …). Un número natural es cualquiera de los números que se usan para contar los elementos de un conjunto. Reciben ese nombre porque fueron los primeros que… … Wikipedia Español
Número ordinal — Representación de los números ordinales hasta ωω. Cada serie de la espiral representa una potencia de ω. En matemáticas, un número ordinal es un número que denota la posición de un elemento perteneciente a una sucesión ordenada. Por ejemplo, en… … Wikipedia Español
Cardinal de una unión de conjuntos — Saltar a navegación, búsqueda Sean los conjuntos: y conociendo el cardinal de cada conjunto: , así como el cardinal de cada intersección de dos, tres, ..., n conjuntos … Wikipedia Español
Número transfinito — En teoría de conjuntos, número transfinito es el término original que el matemático alemán Georg Cantor introdujo para referirse a los ordinales infinitos, esto es, mayor que cualquier número natural o finito, para diferenciarlos del infinito… … Wikipedia Español
Conjuntos numéricos — Uno o varios wikipedistas están trabajando actualmente en este artículo o sección. Es posible que a causa de ello haya lagunas de contenido o deficiencias de formato. Si quieres, puedes ayudar y editar, pero por favor: antes de realizar… … Wikipedia Español
Número de Hartogs — En matemáticas, en particular en la teoría axiomática de conjuntos, un número de Hartogs es un tipo particular de número cardinal. En 1915, Friedrich Hartogs demostró que basta con los axiomas de Zermelo Fraenkel (es decir, no se requiere el… … Wikipedia Español
Número — (Del lat. numerus.) ► sustantivo masculino 1 MATEMÁTICAS Ente abstracto o expresión de la cantidad en relación con la unidad. 2 MATEMÁTICAS Signo o conjunto de signos con que se representa este ente abstracto. SINÓNIMO cifra guarismo 3 Cantidad… … Enciclopedia Universal
Número cuántico — Representación clásica de un átomo en los modelos de Rutherford y Bohr. Los números cuánticos son unos números que se conservan en los sistemas cuánticos. Corresponden con aquellos observables que conmutan con el Hamiltoniano del sistema. Así,… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Número cardinal (teoría de conjuntos)

Contenido

Introducción histórica

Equipotencia