Axioma de regularidad

Axioma de regularidad

Axioma de regularidad

El axioma de regularidad o axioma de fundación es un axioma de la Teoría de Conjuntos (enmarcada en su formulación de Zermelo-Fraenkel-Skolem). Es conocido usualmente como V = R. Fue establecido por Zermelo en 1930 (si bien Von Neumann había propuesto en 1929 uno similar de formulación más compleja).

Enunciado

Podemos enunciar el axioma de regularidad afirmando que dado un conjunto no vacío x, existe siempre algún elemento suyo 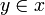y \in x de manera que es disjunto con x. Formalmente: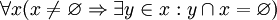

\forall x (x \neq \varnothing \Rightarrow \exists y \in x : y \cap x = \varnothing)

Usos

El axioma de regularidad es un axioma de tipo técnico, es decir, su uso es muy restringido en Teoría de Conjuntos, y fue formulado ad hoc para evitar ciertas paradojas. Pero una de las conclusiones más importantes que produce es la de que cualquier conjunto puede obtenerse a partir del conjunto vacío mediante la reiterada aplicación de la potenciación de conjuntos (es decir, la operación entre conjuntos que a un conjunto x le asigna el conjunto de las partes de x: 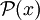\mathcal{P}(x)). 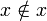También prohíbe la existencia de un conjunto que se tuviera a sí mismo como elemento, es decir se cumple gracias a él que si x es un conjunto, entonces x \notin x.

Obtenido de "Axioma de regularidad"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать курсовую

Mira otros diccionarios:

  • Axiomas de Zermelo-Fraenkel — Los axiomas de Zermelo Fraenkel, formulados por Ernst Zermelo y Adolf Fraenkel, son un sistema axiomático concebido para formular la teoría de conjuntos. Normalmente se abrevian como ZF o en su forma más común, complementados por el axioma de… …   Wikipedia Español

  • Par ordenado — Saltar a navegación, búsqueda Un par ordenado es una tupla de dos elementos, tal que uno puede ser distinguido como el primero y el otro como el segundo. Un par ordenado con primer elemento a y segundo b es escrito usualmente como (a, b). Dos… …   Wikipedia Español

  • Número ordinal — Representación de los números ordinales hasta ωω. Cada serie de la espiral representa una potencia de ω. En matemáticas, un número ordinal es un número que denota la posición de un elemento perteneciente a una sucesión ordenada. Por ejemplo, en… …   Wikipedia Español

  • Relación bien fundada — En teoría de conjuntos, una relación bien fundada sobre una clase X es una relación binaria R sobre X tal que todo subconjunto no vacío de X tiene un elemento R mínimo; esto es: Para todo subconjunto no vacío S de X, hay un elemento m en S tal… …   Wikipedia Español

  • Conjunto singular — Se llama conjunto singular en la teoría de conjuntos a todo conjunto que se contiene a sí mismo. Este tipo de conjuntos es la base de ciertas paradojas matemáticas que, como la paradoja de Russell o la paradoja del conjunto de todos los conjuntos …   Wikipedia Español

  • Número ordinal (teoría de conjuntos) — Este artículo trata sobre números ordinales en teoría de conjuntos axiomática. Para una introducción más básica, véase Número ordinal. Representación del ordinal ωω. Cada vuelta alrededor de esta espiral representa una potencia entera de ω: la… …   Wikipedia Español

  • Espacio vectorial — Saltar a navegación, búsqueda Un espacio vectorial es un conjunto de objetos (llamados vectores) que pueden escalarse y sumarse. Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra… …   Wikipedia Español

  • Teoría de conjuntos de Morse-Kelley — La teoría de conjuntos de Morse Kelley (MK) es una teoría axiomática de conjuntos. Es similar a la teoría de Von Neumann Bernays Gödel, pero MK es más potente y no son equivalentes. Contenido 1 Axiomas 1.1 Ontología y notación 1.2 Axiomas… …   Wikipedia Español

  • Teoría de conjuntos de Von Neumann-Bernays-Gödel — La teoría de conjuntos de von Neumann Bernays Gödel (NBG) es una teoría de conjuntos axiomática. Su noción primitiva es la de clase, en lugar de conjunto como en ZF. A diferencia de otras teorías de conjuntos, NBG es finitamente axiomatizable.… …   Wikipedia Español

  • Albert Einstein — Para otros usos de este término, véase Einstein (desambiguación). Albert Einstein …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”