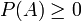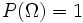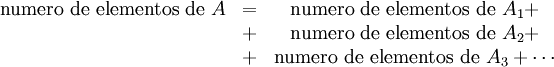Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función que definimos sobre unos sucesos determine consistentemente valores de probabilidad sobre dichos sucesos.

La probabilidad P de un suceso E, denotada por P(E), se define con respecto a un "universo" o espacio muestral Ω, conjunto de todos los posibles sucesos elementales, tal que P verifique los Axiomas de Kolmogórov, enunciados por el matemático ruso de este nombre en 1933. En este sentido, el suceso E es, en términos matemáticos, un subconjunto de Ω.

Contenido 1 Axiomas de Kolmogórov 1.1 Primer axioma 1.2 Segundo axioma 1.3 Tercer axioma 1.4 Propiedades que se deducen de los axiomas 2 Véase también 3 Referencias 4 Enlaces externos

Axiomas de Kolmogórov

Dado un conjunto de sucesos elementales, Ω, sobre el que se ha definida una σ-álgebra (léase sigma-álgebra) σ de subconjuntos de Ω y una función P que asigna valores reales a los miembros de σ, a los que denominamos "sucesos", diremos que P es una probabilidad sobre (Ω,σ) si se cumplen los siguientes tres axiomas.

Primer axioma

La probabilidad de un suceso A es un número real mayor o igual que 0.

La probabilidad de un suceso es un número positivo o nulo.

Segundo axioma

La probabilidad del total, Ω, es igual a 1.

Ω representa todas las posibles alternativas y se denomina suceso seguro.

Tercer axioma

Si A₁, A₂... son sucesos mutuamente excluyentes (incompatibles dos a dos, disjuntos o de intersección vacía dos a dos), entonces:

.

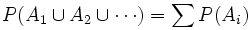Según este axioma se puede calcular la probabilidad de un suceso compuesto de varias alternativas mutuamente excluyentes sumando las probabilidades de sus componentes.

Propiedades que se deducen de los axiomas

De los axiomas anteriores se deducen otras propiedades de la probabilidad:

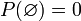1. donde el conjunto vacío 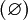representa en probabilidad el suceso imposible
2. Para cualquier suceso
3. 
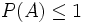
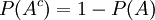
4. Si 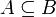entonces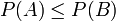
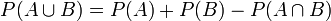
5. 

En términos más formales, una probabilidad es una medida sobre una σ-álgebra de subconjuntos del espacio muestral, siendo los subconjuntos miembros de la σ-álgebra los sucesos y definida de tal manera que la medida del total sea 1. Tal medida, gracias a su definición matemática, verifica igualmente los tres axiomas de Kolmogórov. A la terna formada por el espacio muestral, la σ-álgebra y la función de probabilidad se la denomina Espacio probabilístico, esto es, un "espacio de sucesos" (el espacio muestral) en el que se han definido los posibles sucesos a considerar (la σ-álgebra) y la probabilidad de cada suceso (la función de probabilidad).

Como ejemplo se puede tomar como espacio muestral a los posibles resultados al arrojar un dado corriente 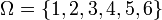, tomaremos como σ-álgebra todos los subconjuntos posibles de Ω (que en matemáticas se denota por 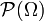) y como función de probabilidad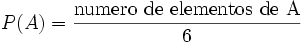

Es fácil comprobar que esta función verifica los tres axiomas de Kolmogórov y, por tanto, consituye una probabilidad sobre este conjunto.

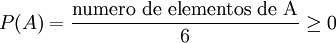1. , puesto que es el cociente de dos números positivos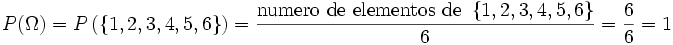
2. 
3. Si 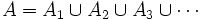de tal manera que 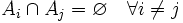entonces

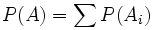
con lo que

Véase también

• Axioma
• σ-álgebra o Sigma-álgebra
• Andréi Kolmogórov
• Teoremas de Probabilidad

Referencias

• Departamento de Matemáticas (Fac. Ing.), Universidad Autónoma de Queretaro, México
• Departamento de Ciencias Físicias y Matemáticas, U. Arturo Prat, Chile

Enlaces externos

• Andréi Nikoláyevich Kolmogórov (en inglés)