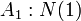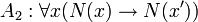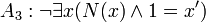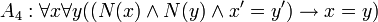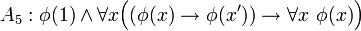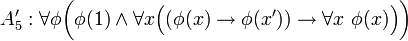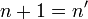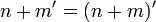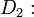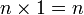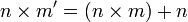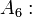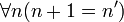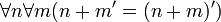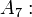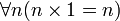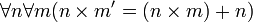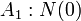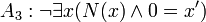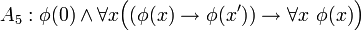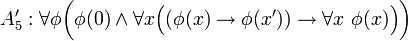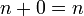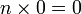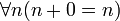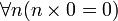Axiomas de Peano

Saltar a navegación, búsqueda

Los axiomas de Peano o postulados de Peano son un conjunto de axiomas para los números naturales introducidos por Giuseppe Peano en el siglo XIX. Los axiomas se han utilizado prácticamente sin cambios para una variedad de investigaciones metamatemáticas, incluyendo cuestiones acerca de la consistencia y completitud en la teoría de números.

Los axiomas de Peano no se ocupan del significado de "número natural", sino que lo suponen y pretenden encontrar un sistema simple de axiomas que caractericen los números naturales y nos permitan deducir a partir de estos, todas las propiedades de los números naturales, utilizando las reglas de la lógica.

Los cinco axiomas de Peano son los siguientes:

El 1 es un número natural.
Si n es un número natural, entonces el sucesor de n también es un número natural.
El 1 no es el sucesor de ningún número natural.
Si hay dos números naturales n y m con el mismo sucesor, entonces n y m son el mismo número natural.
Si el 1 pertenece a un conjunto, y dado un número natural cualquiera, el sucesor de ese número también pertenece a ese conjunto, entonces todos los números naturales pertenecen a ese conjunto. Este es el axioma de inducción, y captura la idea de inducción matemática.

Hay un debate sobre si considerar al 0 como número natural o no. Generalmente se decide en cada caso, dependiendo de si se lo necesita o no. Cuando se resuelve incluir al 0, entonces deben hacerse algunos ajustes menores:

El 0 es un número natural.
Si n es un número natural, entonces el sucesor de n también es un número natural.
El 0 no es el sucesor de ningún número natural.
Si hay dos números naturales n y m con el mismo sucesor, entonces n y m son el mismo número natural.
Si el 0 pertenece a un conjunto, y dado un número natural cualquiera, el sucesor de ese número también pertenece a ese conjunto, entonces todos los números naturales pertenecen a ese conjunto. Este es el axioma de inducción, y captura la idea de inducción matemática.

Contenido

1 Presentación formal
- 1.1 Cuando no se incluye al 0
- 1.2 Cuando se incluye al 0
2 Modelos inintencionales
3 Bibliografia
4 Enlaces externos

Presentación formal

Como se dijo anteriormente, existe un debate sobre si incluir al 0 entre los números naturales o no. A continuación se presentan los axiomas de Peano de manera formal, contemplando ambas posibilidades:

Cuando no se incluye al 0

Los símbolos primitivos son: $<N,1,x'> \,$

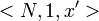
El símbolo N es un predicado monádico que pretende ser leído como "ser un número natural". El símbolo 1, por su parte, es una constante que pretende representar al número uno. Y el símbolo x', finalmente, es una función sobre x que devuelve al sucesor de x. A esta función muchas veces se la escribe "S(x)".

Los cinco axiomas de Peano son:

$A_1: N(1) \,$

$A_2: \forall x (N(x) \to N(x'))$

$A_3: \neg \exists x (N(x) \and 1=x')$

$A_4: \forall x \forall y ((N(x) \and N(y) \and x'=y') \to x=y)$

Del quinto axioma existen dos variantes. El primero está formulado en lógica de primer orden, y es en realidad un esquema de axioma. El segundo sí es un axioma, pero está formulado en lógica de segundo orden.

$A_5: \phi(1) \and \forall x \Big( (\phi (x) \to \phi(x')) \to \forall x \ \phi(x) \Big)$

$A_5': \forall \phi \bigg( \phi(1) \and \forall x \Big( (\phi (x) \to \phi(x')) \to \forall x \ \phi(x) \Big) \bigg)$

Además de los cinco axiomas, la aritmética de Peano recurre a dos definiciones (de la suma y de la multiplicación), que a veces se presentan como axiomas. A continuación se incluyen todas las variantes:

Definiciones de suma y multiplicación:

$D_1: \,$	$n+1=n' \,$
	$n+m'=(n+m)' \,$

$D_2: \,$	$n \times 1 = n \,$
	$n \times m' = (n \times m) + n \,$

Axiomas de la suma y de la multiplicación:

$A_6: \,$	$\forall n (n+1=n')$
	$\forall n \forall m (n+m'=(n+m)')$

$A_7: \,$	$\forall n (n \times 1 = n) \,$
	$\forall n \forall m (n \times m' = (n \times m) + n) \,$

Cuando se incluye al 0

Símbolos primitivos: $<N,0,x'> \,$

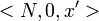
Axiomas:

$A_1: N(0) \,$

$A_2: \forall x (N(x) \to N(x'))$

$A_3: \neg \exists x (N(x) \and 0=x')$

$A_4: \forall x \forall y ((N(x) \and N(y) \and x'=y') \to x=y)$

$A_5: \phi(0) \and \forall x \Big( (\phi (x) \to \phi(x')) \to \forall x \ \phi(x) \Big)$

$A_5': \forall \phi \bigg( \phi(0) \and \forall x \Big( (\phi (x) \to \phi(x')) \to \forall x \ \phi(x) \Big) \bigg)$

Cambiar los axiomas para que incluyan al 0 es sólo una cuestión de cambiar toda aparición del 1 por el 0. Sin embargo, en las definiciones (o los axiomas) de suma y de multiplicación hay que hacer algunos leves ajustes más:

Definiciones de suma y multiplicación:

$D_1: \,$	$n+0=n \,$
	$n+m'=(n+m)' \,$

$D_2: \,$	$n \times 0 = 0 \,$
	$n \times m' = (n \times m) + n \,$

Axiomas de la suma y de la multiplicación:

$A_6: \,$	$\forall n (n+0=n)$
	$\forall n \forall m (n+m'=(n+m)')$

$A_7: \,$	$\forall n (n \times 0 = 0) \,$
	$\forall n \forall m (n \times m' = (n \times m) + n) \,$

Modelos inintencionales

Un modelo es una interpretación de los símbolos primitivos que hace verdaderos a todos los axiomas. Por ejemplo, interpretando al símbolo 0 como el número cero, y al predicado N como los números naturales, el primer axioma resulta verdadero, porque es verdad que "el cero es un número natural". Lo mismo ocurre con todos los otros axiomas: bajo las interpretaciones naturales de 0, N y x', cada uno de los axiomas resulta verdadero. Luego, las interpretaciones naturales de los símbolos primitivos son un modelo de la aritmética de Peano.

Originalmente, los axiomas de Peano fueron diseñados para caracterizar a los números naturales, y los símbolos primitivos debían ser interpretados de esta manera natural. Sin embargo, dado que el significado de los símbolos primitivos no está especificado (por eso son primitivos), admiten varias interpretaciones, algunas de las cuales serán además modelos. Por ejemplo, podría interpretarse al símbolo 0 como el número dos, a N como el predicado "ser un número par", y a x' como el sucesor del sucesor, en vez del sucesor inmediato. En tal caso, los axiomas tendrían que entenderse así:

El dos es un número par
Si n es un número par, entonces el sucesor del sucesor de n también es un número par
El dos no es el sucesor del sucesor de ningún número par.
Si hay dos números pares n y m con el mismo sucesor de sucesor, entonces n y m son el mismo número par.
Si el dos pertenece a un conjunto, y dado un número par cualquiera, el sucesor del sucesor de ese número también pertenece a ese conjunto, entonces todos los números pares pertenecen a ese conjunto.

Bajo esta interpretación, todos los axiomas resultan verdaderos, y los axiomas ya no definen a los números naturales, sino a los números pares. También es posible encontrar modelos (es decir, interpretaciones que hagan verdaderos a todos los axiomas) por fuera de la matemática. Por ejemplo, podría interpretarse a 0 como el primer día de la creación, a N como el predicado "ser un día", y a x' como el día después de x. Bajo esta interpretación, los axiomas también resultan verdaderos.

A aquellos modelos que no fueron originalmente planeados se los llama modelos inintencionales (non intended models), y existen infinitos modelos inintencionales de la aritmética de Peano. Estrictamente hablando, la aritmética de Peano no define a la serie de los números naturales, sino a la noción más amplia de progresión.

Bibliografia

Peano, Giuseppe (marzo de 1979). Velarde Lombraña, Julián (ed.). Los principios de la aritmética: expuestos según un nuevo método., Velarde Lombraña, Julián; tr., 1 edición (en español), Pentalfa Ediciones. ISBN 978-84-85422-02-9.

Enlaces externos

Obtenido de "Axiomas de Peano"

Categoría: Teoría de números

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

Axiomas de Peano — Los axiomas de Peano o postulados de Peano definen de manera exacta al conjunto de los números naturales. Fueron establecidos por Peano (1858 1932), matemático italiano, en el siglo XIX. Básicamente, los naturales se pueden construir a partir de… … Enciclopedia Universal
Axiomas de Zermelo-Fraenkel — Los axiomas de Zermelo Fraenkel, formulados por Ernst Zermelo y Adolf Fraenkel, son un sistema axiomático concebido para formular la teoría de conjuntos. Normalmente se abrevian como ZF o en su forma más común, complementados por el axioma de… … Wikipedia Español
Peano — Peano, axiomas de … Enciclopedia Universal
Peano, axiomas de — ► MATEMÁTICAS Conjunto de axiomas que definen a los números naturales y permiten construir la aritmética como un sistema hipotético deductivo. Los cinco axiomas son: 1) La unidad de un número; 2) el sucesivo de un número es otro número; 3) si a y … Enciclopedia Universal
Giuseppe Peano — Giuseppe Peano. Nacimiento 27 de agosto de 1858 … Wikipedia Español
Teoremas de incompletitud de Gödel — Kurt Gödel a los 19 años de edad, cinco años antes de la demostración de los teoremas. Los teoremas de incompletitud de Gödel son dos célebres teoremas de lógica matemática demostrados por Kurt Gödel en 1930. Ambos están relacionados con la… … Wikipedia Español
Número natural — Los números naturales pueden usarse para contar (una manzana, dos manzanas, tres manzanas, …). Un número natural es cualquiera de los números que se usan para contar los elementos de un conjunto. Reciben ese nombre porque fueron los primeros que… … Wikipedia Español
Sistema formal — La noción de sistema formal se utiliza para proporcionar una definición rigurosa del concepto de demostración en lógica y en matemáticas. La noción de sistema formal corresponde a una formalización rigurosa y completa del concepto de sistema… … Wikipedia Español
Kurt Gödel — Para el lenguaje de programación, véase Gödel (lenguaje de programación). Kurt Gödel Kurt Gödel Nacimiento 28 de abril … Wikipedia Español
Sistema axiomático — En matemáticas, un sistema axiomático consiste en un conjunto de axiomas que se utilizan, mediante deducciones, para demostrar teoremas. Una teoría matemática es un sistema axiomático y, por tanto, todos los teoremas derivados de ellos. Un… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Axiomas de Peano

Axiomas de Peano

Contenido