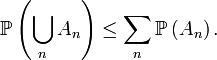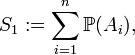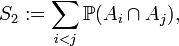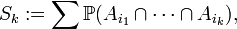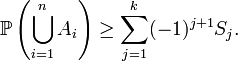Desigualdad de Boole

Desigualdad de Boole

Desigualdad de Boole

En teoría de la probabilidad, la desigualdad de Boole estipula que para toda familia finita o numerable de sucesos, la probabilidad de que al menos uno de esos sucesos ocurra es menor o igual a la suma de las probabilidades de los sucesos individuales. De manera más formal,

Teorema:


Para una familia finita o numerable de sucesos A1, A2, A3, ..., se cumple:
\mathbb{P}\left(\bigcup_{n} A_n\right) \leq \sum_n \mathbb{P}\left(A_n\right).

Contenido

Demostración

Familia finita

Primero se trata, por inducción, el caso de una familia finita 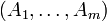(A_1, \dots, A_m) de sucesos.

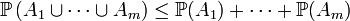Se trata de probar que \mathbb{P}\left(A_1 \cup \cdots \cup A_m\right) \leq \mathbb{P}(A_1) + \cdots + \mathbb{P}(A_m).

La desigualdad es cierta para m = 1. Supuesta cierta para un m dado, se considera una familia 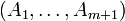(A_1, \dots, A_{m + 1}) de m + 1 sucesos.

Sea 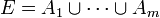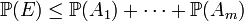E = A_1 \cup \cdots \cup A_m : \mathbb{P}(E) \leq \mathbb{P}(A_1) + \cdots + \mathbb{P}(A_m) (hipótesis de inducción).

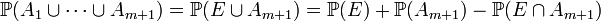Entonces: \mathbb{P}(A_1 \cup \cdots \cup A_{m+1}) = \mathbb{P}(E \cup A_{m+1}) = \mathbb{P}(E) + \mathbb{P}(A_{m+1}) - \mathbb{P}(E \cap A_{m+1}),

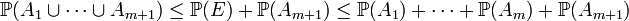de donde: \mathbb{P}(A_1 \cup \cdots \cup A_{m+1}) \leq \mathbb{P}(E) + \mathbb{P}(A_{m+1}) \leq \mathbb{P}(A_1) + \cdots + \mathbb{P}(A_m) + \mathbb{P}(A_{m+1}).

Familia numerable

Ahora se trata el caso de una familia numerable 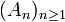(A_n)_{n \geq 1} de sucesos.

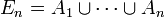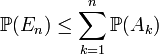Para todo número natural n (distinto de cero), sea E_n = A_1 \cup \cdots \cup A_n; entonces \mathbb{P}(E_n) \leq \sum_{k=1}^n \mathbb{P}(A_k).

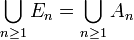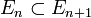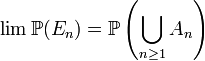La desigualdad de Boole se comprueba por paso al límite sobre n; en efecto \bigcup_{n \geq 1} E_n = \bigcup_{n \geq 1} A_n y para todo n, E_n \subset E_{n+1}, entonces \lim \mathbb{P}(E_n) = \mathbb{P}\left(\bigcup_{n \geq 1} A_n\right).

Otro método

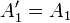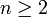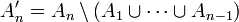Otro método que trata a la vez el caso finito y el caso numerable: sea \ A'_1 = A_1 y para todo n \geq 2, A'_n = A_n \setminus (A_1 \cup \cdots \cup A_{n-1}).

Entonces 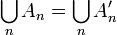\bigcup_{n} A_n = \bigcup_{n} A'_n, y los sucesos 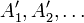A'_1, A'_2, \dots son incompatibles dos a dos;
por otra parte, para todo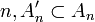 n, A'_n \subset A_n, entonces 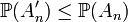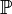\mathbb{P}(A'_n) \leq \mathbb{P}(A_n) (\mathbb{P} es creciente).

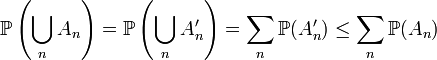De todo esto, se deduce que \mathbb{P}\left(\bigcup_{n} A_n\right) = \mathbb{P}\left(\bigcup_{n} A'_n\right) = \sum_{n} \mathbb{P}(A'_n) \leq \sum_{n} \mathbb{P}(A_n) .

Teoría de la medida

En lenguaje de la teoría de la medida, la desigualdad de Boole se deriva del hecho de que una medida de probabilidad es σ-subaditiva, como es el caso de toda medida.

Desigualdades de Bonferroni

Las llamadas desigualdades de Bonferroni generalizan la desigualdad de Boole y proporcionan mayorantes y minorantes de la probabilidad de uniones finitas de sucesos.

Sean:

S_1 := \sum_{i=1}^n \mathbb{P}(A_i),
S_2 := \sum_{i<j} \mathbb{P}(A_i \cap A_j),

y para 2 < k ≤ n,

S_k := \sum \mathbb{P}(A_{i_1}\cap \cdots \cap A_{i_k} ),

donde la suma de realiza sobre todas las k-uplas estrictamente crecientes de enteros positivos comprendidos entre 1 y n.

Entonces para todo entero positivo impar k tal que 1 ≤ k ≤ n

\mathbb{P}\left( \bigcup_{i=1}^n A_i \right) \leq \sum_{j=1}^k (-1)^{j+1} S_j,

y para todo entero positivo par k tal que 2 ≤ k ≤ n

\mathbb{P}\left( \bigcup_{i=1}^n A_i \right) \geq \sum_{j=1}^k (-1)^{j+1} S_j.

La desigualdad de Boole se da para k = 1.

Véase también

Obtenido de "Desigualdad de Boole#Desigualdades de Bonferroni"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Politopo — Saltar a navegación, búsqueda En geometría politopo significa, en primer lugar, la generalización a cualquier dimensión de un polígono bidimensional, o un poliedro tridimensional. Además, este término es utilizado en varios conceptos matemáticos… …   Wikipedia Español

  • Circuito comparador — Un circuito comparador combinatorio compara dos entradas binarias (A y B de n bits) para indicar la relación de igualdad o desigualdad entre ellas por medio de tres banderas lógicas que corresponden a las relaciones A igual B, A mayor que B y A… …   Wikipedia Español

  • Lógica cuántica — En física, la lógica cuántica es el conjunto de reglas algebraicas que rigen las operaciones para combinar y los predicados para relacionar proposiciones asociadas a acontecimientos físicos que se observan a escalas atómicas. Ejemplos de tales… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”