Análisis de nodos

Figura 1: La ley de corrientes de Kirchhoff es la base del análisis de nodos.

En análisis de circuitos eléctricos, el análisis de nodos, o método de tensiones nodales es un método para determinar la tensión (diferencia de potencial) de uno o más nodos.

Cuando se analiza un circuito por las leyes de Kirchhoff, se podrían usar análisis de nodos (tensiones nodales) por la ley de corrientes de Kirchhoff (LCK) o análisis de malla (corrientes de malla) usando la ley de tensiones de Kirchhoff (LVK). En el análisis de nodos se escribe una ecuación para cada nodo, con condición que la suma de esas corrientes sea igual a cero en cualquier instante, por lo que una carga nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por la conductancia. Por ejemplo, para un resistor, I_rama = V_rama * G, donde G es la Conductancia del resistor.

El análisis de nodos es posible cuando todos los nodos tienen conductancia. Este método produce un sistema de ecuaciones, que puede resolverse a mano si es pequeño, o también puede resolverse rápidamente usando álgebra lineal en un computador. Por el hecho de que forme ecuaciones muy sencillas, este método es una base para muchos programas de simulación de circuitos (Por ejemplo, SPICE). Cuando los elementos del circuito no tienen conductancia, se puede usar una extensión más general del análisis de nodos, El análisis de nodos modificado.

Los ejemplos simples de análisis de nodos se enfocan en elementos lineales. Las redes no lineales(que son más complejas) también se pueden resolver por el análisis de nodos al usar el método de Newton para convertir el problema no lineal en una secuencia de problemas lineales.

Procedimiento

Figura 2: Se elige el nodo con más conexiones como nodo de referencia (cuya tensión es 0) y se asignan 3 variables V_a, V_b y V_c

1. Localice los segmentos de cable conectados al circuito. Estos serán los nodos que se usarán para el método.
2. Seleccione un nodo de referencia (polo a tierra). Se puede elegir cualquier nodo ya que esto no afecta para nada los cálculos; pero elegir el nodo con más conexiones podría simplificar el análisis.
3. Identifique los nodos que están conectados a fuentes de voltaje que tengan una terminal en el nodo de referencia. En estos nodos la fuente define la tensión del nodo. Si la fuente es independiente, la tensión del nodo es conocida. En estos nodos no se aplica la LCK.
4. Asigne una variable para los nodos que tengan tensiones desconocidas. Si la tensión del nodo ya se conoce, no es necesario asignarle una variable. (Véase Figura 2)
5. Para cada uno de los nodos, se plantean las ecuaciones de acuerdo con las Leyes de Kirchhoff. Básicamente, sume todas las corrientes que pasan por el nodo e igualelas a 0. Si el número de nodos es n, el número de ecuaciones será por lo menos n − 1 porque siempre se escoge un nodo de referencia el cual no se le elabora ecuación.
6. Si hay fuentes de tensión entre dos tensiones desconocidas, una esos dos nodos como un supernodo. Las corrientes de los dos nodos se combinan en una nueva ecuación muy sencilla.
7. Resuelva el sistema de ecuaciones simultáneas para cada tensión desconocida.

Ejemplos

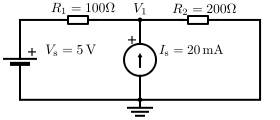
Ejemplo 1: Caso básico

Figura 3: Circuito sencillo con una tensión desconocida V₁.

La única tensión desconocida en este circuito es V₁. Hay tres conexiones en este nodo y por esta razón, 3 corrientes a considerar. Ahora se analiza todas las corrientes que pasan por el nodo, así:

Con ley de corrientes de Kirchhoff (LCK), tenemos:

Se resuelve con respecto a V₁:

Finalmente, la tensión desconocida se resuelve sustituyendo valores numéricos para cada variable. Después de haber obtenido estas ecuaciones y conocer cada tensión, es fácil calcular cualquier corriente desconocida.

Ejemplo 2

Figura 4: Gráfico del Ejemplo 2

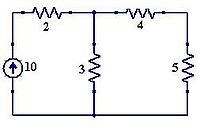
Ejemplo: Del circuito de la figura 4 debemos hallar los voltajes en sus diferentes nodos'

Solución:

1. Se localizan todos los nodos del circuito.
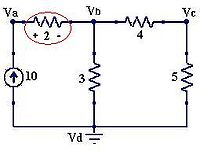
2. Se busca el nodo con más conexiones y se le llama nodo de referencia V_d (Figura 5).
3. No hay fuentes de tensión.
4. Se le asignan variables a los nodos V_a, V_b y V_c
5. Se plantean las ecuaciones según las leyes de Kirchhoff, así:
   • Para calcular el voltaje en el nodo Va, decimos que la resistencia de 2Ω tiene la polaridad de la Figura 5. Así

Figura 5

simplificando:

• Para calcular el voltaje en el segundo nodo (Vb) las resistencias que van a dicho nodo tendrán la polaridad de la Figura 6:

Figura 6

factorizando obtenemos

• Para la polaridad del nodo Vc asumimos así:

Figura 7

factorizando obtenemos:

Sistema de ecuaciones: Obtenemos un sistema de ecuaciones del cual podemos determinar los valores del los voltajes en los nodos.

Solucionando el sistema lineal, nos da como resultado los voltajes: V_a = 42.5V, V_b = 22.5V y V_c = 12.5V

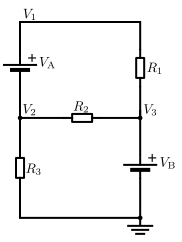
Supernodos

Figura 8: En este circuito, V_A está en medio de dos tensiones desconocidas, y además es un supernodo.

En este circuito, inicialmente tenemos dos tensiones desconocidas, V₁ y V₂. La tensión en la terminal positiva de V_B ya se conoce porque la otra terminal se encuentra en el nodo de referencia. La corriente que pasa por la fuente de voltaje V_A no puede ser calculada directamente. Además no podemos escribir las ecuaciones de corriente para V₁ y ₂. Incluso si los nodos no pueden resolverse individualmente, sabemos que la combinación de estos nodos es cero. Esta combinación de los dos nodos es llamada el método de supernodo, y requiere una ecuación adicional, que involucre las tensiones que afectan a la fuente, V₁ = V₂ + V_A.

El sistema de ecuaciones para este circuito es:

Al sustituir V₁ en la primera ecuación y resolviendo con respecto a V₂, tenemos:

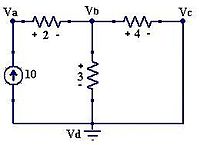
Ejemplo de resolución por supernodos

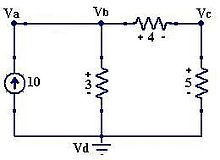
Figura 9: Ejemplo de supernodo

Para calcular la tensión entre las terminales de la fuente de tensión, sumamos las tensiones de las resistencias que están unidas a estos nodos, y además consideramos los dos nodos de la fuente de tensión como uno solo, así:

• Tensión en la resistencia de 4Ω:

factorizando

• Observamos el supernodo en los nodos V_b y V_c, tomamos estos dos nodos como uno solo, por lo tanto sumamos las corrientes de las resistencias que hay conectadas a

V_b y V_c:

factorizando

• Finalmente, planteamos una ecuación para la fuente de voltaje la cual es la caída de voltaje en los nodos así:

V_b − V_c = 10

Observación:Debemos tener en cuenta la polaridad de la fuente para plantear esta última ecuación, y así obtener el sistema de ecuaciones para determinar los valores de los voltajes.

Sistema de ecuaciones:

Resolviendo V_a= 62,5 V, V_b= 22,5 V y V_c= 12,5 V

Enlaces externos

• Análisis de nodos
• Análisis de nodos

Referencias

• Este artículo fue creado a partir de la traducción del artículo Nodal analysis de la Wikipedia en inglés, concretamente de esta versión, bajo licencia Creative Commons Atribución Compartir Igual 3.0 y GFDL.

Enlaces externos

Análisis de nodo