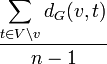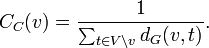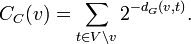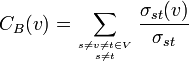Un ejemplo de centralidad se muestra en el grafo de la ilustración, la intermediación se grada mediante colores que van desde el rojo con un bajo valor de intermediación hasta el azul con un valor máximo.

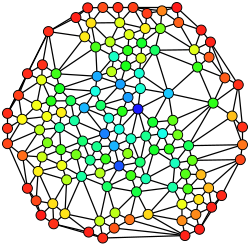
Dentro de la teoría de grafos y del análisis de redes existen ciertos conjuntos de medidas denominadas de centralidad de un vértice en un grafo que determinan la importancia relativa de un vértice en el grafo,^[1] como por ejemplo, la importancia de una persona involucrada en una red social, o, en la teoría de la denominada sintaxis del espacio que se estudia lo importante que puede llegar a ser una habitación en un edificio, así como una carretera en una red urbana.

En algunas ocasiones se han introducido las medidas de centralidad con la intención de detectar componentes esenciales en redes de computadoras. El concepto fue introducido inicialmente por Bavelas en los años 50.^[2] Se trata de uno de los conceptos más estudiados en el análisis de redes ya desde finales de los años 70 en el área de las redes sociales.^{[3] [4]} algunos autores han empleado las medidas de centralidad en relación con el flujo de información en diversas redes,^[1] así como también de bienes usados, movimiento de dinero, propagación de rumores, e-mails, diseminación de actitudes, propagación de infecciones y movimiento de paquetes.

Concepto

La centralidad es un atributo estructural de los nodos en una red, no se trata de un atributo intrínseco de los actores como puede ser el ingreso monetario, la autoestima, la temperatura, etc. se trata de un valor asignado al nodo debido a su posición estructural en la red. De una forma u otra se trata de la contribución de un nodo a la posición que ocupa en la red, bien sea en forma de importancia, influencia, relevancia o prominencia. Por ejemplo en un grafo en forma de estrella, el nodo central ocupa un valor máximo de centralidad, mientras que los nodos de las puntas ocupan un valor de centralidad inferior. Desde la formulación realizada por Bavelas,^[2] se han propuesto diversas medidas de la centralidad de un nodo. Algunas de las más estudiadas en la literatura son:

• Grado nodal - Se trata de la primera y más simple definición de centralidad. Se define como el número de enlaces que posee un nodo con otros. Suele representarse con una letra "k". El grado se interpreta a menudo como el número de conexiones que posee una persona en una red social.
• Cercanía (centralidad) - Tal y como definió Freeman^[3] la cercanía de un nodo (node’s closeness centrality) es la suma de las distancias en un grafo de todos los nodos de la red, donde la distancia de un nodo a otro se define como la longitud (en enlaces) del camino más corto de un nodo a otro. En un contexto de flujo se suele interpretar como el tiempo de llegada de algo que fluye a través de la red.^[1] Mide de alguna forma la accesibilidad de un nodo respecto a otro.
• Intermediación – Denominado también carga, es una medida de la centralidad que indica la frecuencia con la que un nodo aparece en el camino más corto que conecta otros dos nodos. esta medida indica el control del flujo y de la misma forma la capacidad de mantener separadas las diversas partes de una red
• Autovalor – El nodo que posee un valor alto de esta medida de centralidad viene a indicar que está conectado a muchos nodos que a su vez estén bien conectados.

Se pueden distinguir entre las medidas absolutas de centralidad que indican un valor no comparable y aquellas que se normalizan (medidas relativas de centralidad).

Grado

El número de nodos enlazados con uno dado es el grado, por ejemplo el número de amistades de una persona es el grado de esa persona en la red social. A veces se denomina también como conectividad. Se suele representar como la suma de los elementos de una fila (o columna) en la matriz adyacente. Por regla general en la literatura se representa como una letra k_i indicando el número de enlaces que posee el nodo i, de esta forma se tiene que:

Donde a_ij son los coeficientes de la matriz adyacente. Existen variantes de este valor de centralidad como puede ser el grado normalizado obtenido del grado k_i dividido entre el máximo grado obtenido de la red. Este valor viene a indicar la "popularidad" que tiene el nodo en la red en el caso de una red social, para el caso de una red de infección es el grado de riesgo de ser contagiado (grupo de riesgo) o el índice de exposición, y si se tratara de la propagación de un rumor en una red sería la probabilidad de obtener la información vía un rumor. A veces se interpreta como la oportunidad de influir o de ser influido directamente por otros nodos.

Cercanía

Definido en inglés como “closeness”, el matemático Beauchamp define por primera vez la cercanía en una red social en los años 60.^[5] Es empleado como la suma de la suma de las distancias de un nodo con respecto a sus vecinos. En topología y áreas relacionadas con las matemáticas la “cercanía” es interpretada como uno de los conceptos más básicos en el estudio de los espacios topológicos. De forma intuitiva se puede decir que dos conjuntos están próximos si ambos están arbitrariamente cerca uno de otro. El concepto puede ser definido de forma natural en un espacio métrico, donde se puede definir una distancia entre los elementos del espacio, esta definición puede ser generalizada a aquellos espacios topológicos donde no exista una definición concreta de cómo medir distancias. En Teoría de grafos la cercanía es una medida de centralidad asignada a un vértice en un grafo. Los vértices que son ‘poco profundos’ a otros vértices (es decir que poseen distancias geodésicas pequeñas a otros vértices en el grafo) tienen una gran cercanía. La cercanía es una de las medidas preferidas en el análisis de redes ya que viene a usarse en la definición de caminos de poco recorrido, por eso es empleado con otras medidas de centralidad junto con el grado.

En la teoría de grafos la “cercanía” es una sofisticada medida de centralidad. Definida como la distancia geodésica media (como puede ser el problema del camino más corto) entre un vértice v y otros vértices alcanzables desde él:

Donde 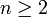es el tamaño de la conectividad de la red desde el vértice v. La cercanía puede ser empleada como una medida de cuanto de largo puede llevar la diseminación de la información desde un vértice dado hasta cualquier otro vértice de la red.^[6]

Algunos autores definen la cercanía como el valor recíproco de esta cantidad, pero ocurre al igual que en física al definir la velocidad, menor espacio menos tiempo en recorrer, más espacio más tiempo a igual velocidad. La cercanía C_C(v) de un vértice v es el valor recíproco de la suma de las distancia geodésicas a los otros vértices de V:^[7]

Existen diferentes métodos y algoritmos para medir la cercanía, uno de ellos es el denominado método de centralidad por camino aleatorio (random-walk centrality) introducido por Noh y Rieger (2003) que se emplea para medir la velocidad en la que un mensaje se propaga por la red si éste posee un camino aleatorio a través de los vértices de la red.^[8]

Otra medida es la centralidad de la información definida por Stephenson y Zelen (1989) como otra variante de medida de la cercanía, esta medida posee cierta similaridad con el método descrito por Noh y Rieger. En esencia mide la longitud media armónica de los caminos que acaban en un vértice i, que sera pequeño si i tiene muchos caminos cortos conectándose con otros vértices.^[9]

Dangalchev (2006), para medir la vulnerabilidad en las redes, modifica la definición de cercanía para poder tratar de analizar los grafos desconectados y hacer que sea más fácil de calcular.^[10] :

Intermediación

En inglés se denomina betweenness es una medida de la centralidad que viene a indicar la frecuencia con la que un nodo aparece en el camino más corto que conecta otros dos nodos, a dicho camino se le suele denominar camino geodésico. Un actor que se encuentra en el camino geodésico que uno dos puntos de la red posee una posición de intermediario, de controlador del flujo de información. En el caso de redes de comunicación la distancia a otras unidades (cercanía) no es la única medida de centralidad importante, es importante saber cuantos caminos de pequeña distancia corren a través de un par de vértices, ya que estas unidades poseen el control del flujo sobre toda la red.

Existe una definición formal en la teoría de grafos donde si se tiene un grafo G: = (V,E) con n vértices, la intermediación C_B(v) para los vértices v es:

donde σ_st es el número de caminos geodésicos desde s a t, y σ_st(v) es el número de trayectos geodésicos desde s a t que pasan a través del vértice v. Este valor puede ser normalizado al dividir entre el número de pares de vértices que no incluyen a v, lo que se representa como (n − 1)(n − 2). En un proceso de difusión el nodo con un valor de intermedicación alto podría controlar el flujo de información llegando a actuar como “guardian”, un proceso de intercambio entre dos nodos con un alto valor de intermedicación puede actuar como un broker. El cálculo de la intermediación y de la cercanía de todos los vértices de un grafo lleva a calcular la distancia mínima de todos los vértices de un grafo. Esto toma un valor de Θ(V³) debido a la aplicación del algoritmo de Floyd-Warshall. En un grafo disperso, el algoritmo de Johnson podría ser muy eficiente, pudiendo llegar a obtener valores de O(V²logV + VE).

Centralidad por autovalor

La idea de autovalor (en inglés “eigenvalue”) fue propuesta como medida central por Phillip Bonacich en 1972.^[11] Este valor viene a indicar la popularidad de un nodo, debido a que expresa el nodo de la red que posee una conexión más alta a otros nodos que están a su vez bien conectados. Supone una medida del centro de grandes grupos cohesivos. En la difusión de información el actor que posee un valor alto en la centralidad de autovalor se dice que está conectado a otros muchos actores que a su vez están bien conectados, por esta razón son buenos nodos para divulgación de rumores, o de enfermedades. En el caso del grado como medida de centralidad se puede ver que cada nodo ‘pesa’ igual, en el caso del autovalor la conexión de los nodos pesa de forma diferente. Desde un punto de vista formal se puede decir que se trata de un principal autovalor asociado a la matriz adyacente de un grafo.

Estudios sobre centralidad

Se han hecho estudios dentro de la teoría de análisis de redes sociales detallando temas como el prestigio, influencia (un nodo con influencia comanda a otros nodos), ayuda, confianza (temas electorales), etc.

Referencias

Véase también

• Teoría de grafos
• Mundo pequeño