- Número de osculación
-
En geometría, el número de osculación es el máximo número de esferas de radio 1 que pueden tocar simultáneamente a la esfera unitaria en un espacio euclídeo n-dimensional. El problema del número de osculación pretende obtener el número de esferas como una función de n (dimensión del espacio).
Contenido
Números de Osculación conocidos
 El número de osculación en dimensión 1 es 2.
El número de osculación en dimensión 1 es 2.
- En dimensión 1, el número de osculación es, de modo obvio, 2:
- En dimensión 2, es sencillo ver y probar que el número de osculación es 6.
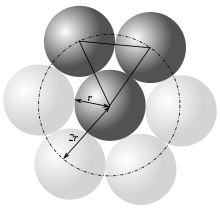
- En dimensión 3 la respuesta ya no es tan sencilla. Podemos disponer fácilmente 12 esferas de modo que cada una esté en contacto con la central, pero queda mucho espacio libre entre unas y otras, de modo que no es obvio que no haya forma de colocar la esfera número 13. Este fue un tema de controversia entre los matemáticos Isaac Newton y David Gregory. Newton pensaba que el límite era 12 y Gregory que era 13. La cuestión no se resolvió hasta 1874: Newton tenía razón.[1]
- En dimensión 4, durante un tiempo se ignoró si la solución era 24 o 25. En 2003, Oleg Musin probó que la solución correcta era 24.[2]
- En dimensión n, con n > 4, se desconoce la respuesta excepto para n = 8 (240), y n = 24 (196560).[3] [4]
Algunos límites conocidos
La tabla siguiente lista algunos de los límites conocidos de los números de osculación en varias dimensiones. Las dimensiones en las que se conocen los números de osculación están listadas en negrita.
Dimensión Límite
MínimoLímite
Máximo1 2 2 6 3 12 4 24 5 40 45 6 72 78 7 126 135 8 240 9 306 366 10 500 567 11 582 915 12 840 1,416 13 1,130 2,233 14 1,582 3,492 15 2,564 5,431 16 4,320 8,313 17 5,346 12,215 18 7,398 17,877 19 10,688 25,901 20 17,400 37,974 21 27,720 56,852 22 49,896 86,537 23 93,150 128,096 24 196,560 Referencias
- ↑ Conway, John H.; Neil J.A. Sloane (1999). Sphere Packings, Lattices and Groups (3rd ed. edición). New York: Springer-Verlag. ISBN 0-387-98585-9.
- ↑ «Kissing numbers, sphere packings, and some unexpected proofs», Notices of the American Mathematical Society: 873–883, September 2004, http://www.ams.org/notices/200408/fea-pfender.pdf.
- ↑ Levenshtein, V. I. Boundaries for packings in n-dimensional Euclidean space. (Russian) Dokl. Akad. Nauk SSSR 245 (1979), no. 6, 1299—1303
- ↑ Odlyzko, A. M., Sloane, N. J. A. New bounds on the number of unit spheres that can touch a unit sphere in n dimensions. J. Combin. Theory Ser. A 26 (1979), no. 2, 210—214
Véase también
Wikimedia foundation. 2010.