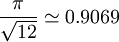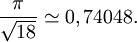El empaquetamiento de esferas tiene aplicación practica en el almacenamiento de naranjas

En matemáticas los problemas de empaquetamiento de esferas conciernen en la disposición de esferas de idéntico tamaño rellenando un espacio. Normalmente el espacio es el euclideo tridimensional. Sin embargo el problema puede generalizarse a dos dimensiones (donde las esferas son círculos), a espacios n-dimensionales (donde son hiperesferas) o a espacios no euclidianos como el espacio hiperbólico.

Un problema típico de empaquetamiento es encontrar la disposición en que las esferas rellenen la mayor proporción posible del espacio. La proporción del espacio rellenado por las esferas es llamada densidad del empaquetamiento. Como la densidad de empaquetamiento puede depender del volumen en que se mida, el problema trata normalmente de la densidad media mayor o asintótica, medida en un volumen lo suficientemente amplio.

Un empaquetamiento habitual también llamado periódico o reticular es aquel en que las esferas forman un patrón muy simétrico llamado retículo, los empaquetamientos en los que las esferas no están dispuestas en patrones simétricos se llaman irregulares o aperiódicos. Las disposiciones periódicas son más sencillas de analizar, clasificar y de medir su densidad que las aperiódicas.

Empaquetamiento de circulos

La mejor forma de empaquetar circulos de diferente tamaño no resulta obvia

El centro de los tres circulos en contacto forma un triangulo equilatero, lo que genera un empaquetamiento hexagonal

Carl Friedrich Gauss demostró que, en espacio euclideo de dos dimensiones, la disposición regular de circulos con mayor densidad es el empaquetamiento hexagonal, en el cual los centros de los circulos se disponen en una celda hexagonal (dispuestas como en un panal de colmena) y en la que cada circulo está rodeado de otros seis. La densidad de este empaquetamiennto es:

En 1940 el matemático húngaro László Fejes Tóth demostró que la celda hexagonal es el más denso de todos los empaquetamientos de circulos, tanto regulares como irregulares.

La rama de las matemáticas conocida como "empaquetamiento de circulos" no se refiere, sin embargo al calculo de la densidad en empaquetamiento de circulos iguales, sino que se refiere a problemas de geometría y combinatoria de circulos de tamaño arbitrario, dando lugar a análogos discretos de la cartografía conforme, las superficies de Riemann y similares.

Empaquetamiento de esferas

Empaquetamiento periódico

apilamiento compacto de 35 esferas

deux manières d'empiler trois plans compacts

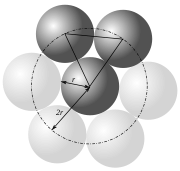
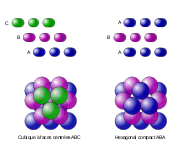
Estudiemos en un espacio tridimensional un plano con una disposición compacta de esferas sobre el mismo. Si consideramos tres esferas vecinas, podremos colocar una cuarta en el hueco que dejan las tres esferas de abajo. Si repetimos esto "en todas partes" en un segundo nivel por encima del primero, habremos creado una nueva disposición compacta. La tercera capa se puede superponer a la primera, o las esferas pueden estar encima de los huecos de la primera capa. Por lo tanto, existen tres tipos de niveles, llamados A, B y C.

Gauss demostró que estas disposiciones poseen la densidad más alta entre todas las disposiciones regulares.

Las dos disposiciones más comunes son llamadas empaquetamiento cúbico centrado en caras – alternancia ABCABC...- y empaquetamiento hexagonal – alternancia ABAB...-. Pero todas las combinaciones son posibles (ABAC, ABCBA, ABCBAC, etc.) En todas estas disposiciones cada esfera está rodeada por otras 12, y ambas disposiciones tienen una densidad media de

En 1611 Johannes Kepler había conjeturado que esta es la densidad máxima de las disposiciones tanto regular como irregular – esto fue conocido como la conjetura de Kepler. En 1998 Thomas Hales, siguiendo el enfoque que había propuesto László Fejes Tóth en 1953, anunció la confirmación de la conjetura de Kepler. La confirmación de Hales es una Prueba por exhaución ensayando muchos casos individuales y usando complejos cálculos de ordenador. Los árbitros han confirmado la exactitud de la prueba de Hales con un margen del "99% de seguridad", por lo que la conjetura de Kepler ha sido demostrada casi con absoluta certeza.

Empaquetamiento aperiódico

Si intentamos construir un grupo densamente empaquetado de esferas, siempre caeremos en la tentación de colocar la siguiente esfera en un hueco formado entre tres esferas en contacto. Si cinco esferas se han reunido en este modo, estará en consonancia con uno de los envasados de disposición regular descritos con anterioridad. Sin embargo, la sexta esfera colocada de esta manera, hace que la estructura sea incompatible con cualquier disposición regular. (Chaikin, 2007). Esto se traduce en la posibilidad de un empaquetamiento aleatorio de las esferas que se torna estable contra la compactación.

Cuando se arrojan esferas al azar en un contenedor y luego se compactan, generalmente forman lo que se conoce como empaquetamiento "irregular" o "atascado", cuando no se puede comprimir más. Este empaquetamiento irregular tendrá normalmente una densidad de aproximadamente el 64% de la densidad de las esferas. Esta situación es diferente al caso de una o dos dimensiones, donde la compactación de un grupo de esferas unidimensionales o bidimensionales (es decir segmentos de línea o discos) producirá un empaquetamiento regular.

Empaquetamiento de hiperesferas

En dimensiones superiores a tres, el empaquetamiento denso regular de hiperesferas que se conoce llega hasta 8 dimensiones. Se sabe muy poco sobre empaquetamiento irregular hiperesférico - es posible que en algunos dimensiones la forma de empaquetamiento más denso pueda ser irregular. El apoyo a esta conjetura proviene del hecho de que en ciertas dimensiones (por ejemplo 10) el empaquetamiento irregular más denso conocido es mejor que el empaquetamiento regular más denso conocido.

La dimensión 24 es especial debido a la existencia de la red de Leech, que tiene el mejor número de osculación (esferas en contacto) y durante mucho tiempo se sospechó que era la celosía de empaquetamiento más densa. En 2004, Cohn y Kumar¹ publicaron un estudio preliminar probando esta conjetura, y, además, demostraron que el empaquetamiento irregular puede mejorar el empaquetamiento de la celosía de Leech, en su caso, en no más de 2 × 10-30.

Otra línea de investigación en dimensiones elevadas está tratando de encontrar límites asintóticos al empaquetamiento más denso. En la actualidad, el mejor resultado conocido es un enrejado en la dimensión n con una densidad mayor o igual a cn2 -n para algunos números c.

Espacio hiperbólico

Aunque el concepto de círculos y esferas puede ampliarse a espacios hiperbólicos, la búsqueda del empaquetamiento más denso se hace mucho más difícil. En un espacio hiperbólico, no hay límites para el número de esferas que pueden rodear otra esfera (por ejemplo, los círculos de Ford pueden ser vistos como una disposición de círculos hiperbólicos idénticos en la que cada círculo está rodeado por un número infinito de otros círculos). El concepto de densidad media se convierte también en algo mucho más difícil de definir con precisión.

A pesar de estas dificultades, Charles Radin y Lewis Bowen, de la Universidad de Texas en Austin mostraron en mayo de 2002 que el empaquetamiento más denso en cualquier espacio hiperbólico es casi siempre irregular.

Otros espacios

El empaquetamiento esférico en las esquinas de un hipercubo (con las esferas definidas por la (distancia de Hamming) corresponde a la elaboración de códigos de corrección de errores: si las esferas tienen radio d, entonces sus centros son la clave de un código de corrección de errores d. Empaquetamientos de celosía equivalen a códigos lineales. Hay otras relaciones más sutiles entre empaquetamiento de ámbito euclidiano y los códigos de corrección de errores; Por tanto, el código binario de Golay está estrechamente relacionado con la dimensión 24 de la red de Leech.

Véase también

• Número de osculación
• Conjetura de Kepler
• Estructura de Weaire-Phelan

Referencias

• Conway, J.H. & Sloane, N.J.H. (1998) "Sphere Packings, Lattices and Groups" (Third Edition). ISBN 0-387-98585-9
• Lewis Bowen & Charles Radin (2003) "Densest Packings of Equal Spheres in Hyperbolic Space" (pre-print of article in Discrete & Computational Geometry)
• N. J. A. Sloane, The Sphere Packing Problem, Plantilla:Arxiv (A technical survey from 2002).
• C. A. Rogers, Existence Theorems in the Geometry of Numbers, The Annals of Mathematics, 2nd Ser., 48:4 (1947), 994-1002 (The n2 ^{− n} result mentioned above. Despite 60 years of research, only the constant was improved in this result).
• Henry Cohn and Abhinav Kumar, The densest lattice in twenty-four dimensions, Plantilla:Arxiv(The solution for the 24 dimensional case).
• T. Aste and D. Weaire "The Pursuit of Perfect Packing" (Institute Of Physics Publishing London 2000) ISBN 0-7503-0648-3
• Chaikin, Paul "Reference Frame", Physics Today, June 2007 p8.

Enlaces externos