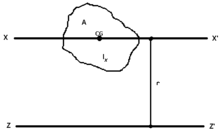
Teorema de Steiner

Teorema de Steiner

En física, el teorema de Huygens-Steiner, teorema de los ejes paralelos o simplemente teorema de Steiner es un teorema usado en la determinación del momento de inercia de un sólido rígido sobre cualquier eje, dado el momento de inercia del objeto sobre el eje paralelo que pasa a través del centro de masa y de la distancia perpendicular]] (r) entre ejes. También puede usarse para calcular el segundo momento de área de una sección respecto a un eje parlelo a otro cuyo momento sea conocido.

Contenido

Enunciado

Momentos de inercia

Dado un eje que pasa por el contro de masa de un sólido, y dado un segundo eje paralelo al primero, el momento de inercia de ambos ejes está relacionado mediante la expresión:

I_{z,P} = I_{z,G} + mr^2,\,

donde:

I_{z,P}\, es el momento de inercia del cuerpo según el eje que no pasa a través de su centro de masas;
I_{z,G}\, es el momento de inercia del cuerpo según un eje que pasa a través de su centro de masas;
m\, es la masa del objeto;
r\, es la distancia perpendicular entre los dos ejes.

El resultado anterior pude extenderse al cálculo completo del tensor de inercia. Dado una base vectorial B el tensor de inercia según esa base respecto al centro de masas y respecto a un punto diferene del centro de masas están relacionados por la relación:

\mathbf{I}_P = \mathbf{I}_G + m \mathbf{d}\otimes\mathbf{d} \quad \Rightarrow \quad I_{ij,P} = I_{ij,G} + m d_i d_j

donde:

\mathbf{d} es el vector con origen en G y extremo en P.

Segundos momento de área

La regla puede ser aplicada con la regla de extensión y el teorema de los ejes perpendiculares para encontrar momentos de inercia de una variedad de formas.

Regla de los ejes paralelos para el momento de inercia

La regla de los ejes paralelos también puede aplicarse al segundo momento de área (momento de inercia planar) para una región plana D:

I_z = I_x + Ar^2,\,

donde:

I_z\! es el momento de inercia planar de D relativo al eje paralelo;
I_x\! es el momento de inercia planar de D relativa a su centroide;
A\! es el área de una región plana D;
r\! es la distancia del nuevo eje zal centroide de la región plana D.

Nota: El centroide de D coincide con el centro de gravedad (CG) de una lámina fija con la misma forma que tiene densidad uniforme.

Tensor de inercia

En mecánica clásica, el teorema de Steiner (también como teorema de Huygens-Steiner) puede ser generalizado para calcular un nuevo tensor de inercia Jij a partir de un tensor de inercia sobre el centro de masas Iij cuando el punto pivotante es un desplazamiento a del centro de masas:

J_{ij}=I_{ij} + m(\|\boldsymbol{a}\|^2 \delta_{ij}-a_ia_j)\!

donde

\boldsymbol{a}=a_1\boldsymbol{\hat{x}}+a_2\boldsymbol{\hat{y}}+a_3\boldsymbol{\hat{z}}\!

es el vector desplazamiento del centro de masas al nuevo eje, y

\delta_{ij}\!

es la función delta de Kronecker.

Se puede ver que, para elementos diagonales (cuando i = j), desplazamientos perpendiculares al eje de rotación resultan en la versión simplificada mostrada arriba del teorema de Steiner.

Demostración

Se asumirá, sin pérdida de generalidad, que en un sistema de coordenadas cartesiano la distancia perpendicular entre los ejes se encuentra a lo largo del eje x y que el centro de masas se encuentra en el origen. El momento de inercia relativo al eje z, que pasa a través del centro de masas, es:

I_{z,cm} = \int{(x^2 + y^2)} dm

El momento de inercia relativo al nuevo eje, a una distancia perpendicular r a lo largo del eje x del centro de masas, es:

I_z = \int{((x - r)^2 + y^2)} dm

Si desarrollamos el cuadrado, se obtiene:

I_z = \int{(x^2 + y^2)} dm + r^2 \int dm - 2r\int{x} dm

El primer término es Icm, el segundo término queda como mr2, y el último término se anula, puesto que el origen está en el centro de masas. Así, esta expresión queda como:

I_z = I_{cm} + mr^2\,

Véase también

  • Teorema de los ejes perpendiculares
  • Regla de extensión
  • Jakob Steiner

Referencias


Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Teorema de Huygens — El teorema de Huygens establece que la longitud reducida de un péndulo físico no varía cuando el centro de oscilación O′ pasa a ser centro de suspensión (O), pues ambos puntos permutan entre sí sus papeles (puntos conjugados). El periodo del… …   Wikipedia Español

  • Steiner — Steiner, George Steiner, Jakob Steiner, teorema de * * * (as used in expressions) Steiner, (Francis) George Steiner, Max(imilian Raoul Walter) Steiner, Rudolf …   Enciclopedia Universal

  • Teorema de Poncelet–Steiner — En geometría, el teorema de Poncelet–Steiner establece que todas las construcciones geométricas que pueden realizarse con regla y compás pueden realizarse únicamente con regla conocido un único círculo y su centro. Por tanto, todas las… …   Wikipedia Español

  • Teorema de Mohr-Mascheroni — En geometría euclídea, el teorema de Mohr Mascheroni establece que todas las construcciones geométricas que pueden realizarse con regla y compás pueden realizarse únicamente con compás. Hay que notar que aunque no puede trazarse con un compás una …   Wikipedia Español

  • Steiner, teorema de — ► MECÁNICA Teorema formulado por J. Steiner que establece que el momento de inercia de un cuerpo respecto de un eje (I) es igual al momento de inercia respecto de un eje paralelo al primero y que pase por el centro de gravedad del cuerpo (I0),… …   Enciclopedia Universal

  • Steiner, Jakob — ► (1796 1863) Matemático y físico suizo. Autor de estudios sobre geometría proyectiva. Enunció el teorema que lleva su nombre …   Enciclopedia Universal

  • Jakob Steiner — Nacimiento 18 de marzo de 1796 Utzenstorf, Cantón de Berna Fallecimiento 1 de abril …   Wikipedia Español

  • Momento de inercia — Para otros usos de este término, véase Momento de inercia (desambiguación). Una bailarina tendrá más momento de inercia si extiende los brazos, girando más rápido si los contrae. El momento de inercia (símbolo I) es una medida de la inercia… …   Wikipedia Español

  • Área triangular — El área triangular es sencillamente el área de un triángulo, el área triangular se caracteriza de las otras áreas de figuras planas por que es la única que tiene tantas fórmulas, además de casos particulares de áreas y también que a partir de las …   Wikipedia Español

  • Péndulo físico — Saltar a navegación, búsqueda Un péndulo físico o compuesto es cualquier cuerpo rígido que pueda oscilar libremente en el campo gravitatorio alrededor de un eje horizontal fijo, que no pasa por su centro de masa. Contenido 1 Deducción del periodo …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”