- Centroide
-
Centroide
En geometría, el centroide o baricentro de un objeto X perteneciente a un espacio n-dimensional es la intersección de todos los hiperplanos que dividen a X en dos partes de igual n-volumen con respecto al hiperplano. Informalmente, es el promedio de todos los puntos de X.
Contenido
Conceptos relacionados
En la Física, el centroide puede, bajo ciertas circunstancias, coincidir con el centro de masas del cuerpo material y con el centro de gravedad del mismo. En esas circunstancias, hay una mala tendencia a utilizar los términos indistantamente, sin prestar atención a lo que realmente nos estamos refiriendo.
Consideremos un cuerpo material:
- Para que el centroide del cuerpo coincida con el centro de masa, el cuerpo tiene que tener densidad uniforme o una distribución de materia que presente ciertas propiedades, tales como la simetría.
- Para que un centro de masa del cuerpo coincida con el centro de gravedad, el cuerpo debe estar bajo la influencia de un campo gravitatorio uniforme.
Una figura cóncava tendrá su centroide en algún punto fuera de la figura misma. El centroide de una lámina con forma de cuarto de Luna estará en algún punto fuera de la lámina.
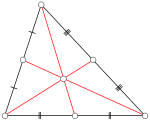
El centroide de un triángulo (también llamado baricentro) se encuentra en el punto donde se intersectan sus medianas (líneas que unen un vértice con el punto medio del lado opuesto). Este punto es también el centroide de la superficie del triángulo.
Centro de simetría
El centroide de un objeto o figura también puede definirse como un punto fijo del grupo de isometría de dicha figura. Para un objeto, figura limitada o región finita el grupo de isometría no incluye traslaciones y en ese caso si el grupo de isometría no es trivial, sus simetrías pueden determinar el centroide.
Sin embargo si para un objeto tiene alguna simetría traslacional el centroide no está definido, porque una traslación no tiene ningún punto fijo.
Véase también
Enlaces externos
Categorías: Geometría euclidiana | Geometría afín | Física | Mecánica
Wikimedia foundation. 2010.