Teselado

Un teselado visto en el pavimento de una Calle

Teselado Hexagonal de un Piso

Un teselado es una regularidad o patrón de figuras que cubre o pavimenta completamente una superficie plana que cumple con dos requisitos:

1. que no queden huecos
2. que no se superpongan las figuras

Los teselados se crean usando transformaciones isométricas sobre una figura inicial.

Distintas culturas en el tiempo han utilizado esta técnica para formar pavimentos o muros de mosaicos en catedrales y palacios.

Es un error común referirse al teselado como "teselación" lo cual es una traducción equivocada de la palabra en Inglés "tesellation". El único término correcto en español es "teselado".

• Algunos mosaicos sumerios con varios miles de años de antigüedad contienen regularidades geométricas.
• Arquímedes en el siglo III a. C. hizo un estudio acerca de los polígonos regulares que pueden cubrir el plano
• Johannes Kepler, astrónomo alemán, estudió los polígonos regulares que pueden cubrir el plano, en su obra “Harmonice mundi” de 1619. Además realizó estudios en tres dimensiones de los llamados sólidos platónicos.
• Entre 1869 y 1891, el matemático Camille Jordan y el cristalógrafo Evgenii Konstantinovitch Fiodorov estudiaron completamente las simetrías del plano, iniciando así el estudio sistemático y profundo de los llamados teselados.
• Un personaje clave en este tema es el artista holandés M. C. Escher (1898-1972) quien, por sugerencia de su amigo el matemático H. S. M. Coxeter, aprendió los teselados hiperbólicos, lo que motivó su interés por el palacio de La Alhambra en Granada. Legó a un sinnúmero de bellas, curiosas y misteriosas obras de arte.

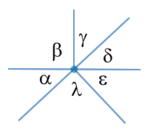ángulos que concurren a un vértice

Conceptos previos

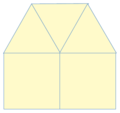
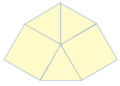
• En un teselado plano la suma de todos los ángulos que concurren a un vértice es 360º.

• Un polígono es regular si tiene todos sus lados y ángulos iguales.
• Un polígono es convexo si todas sus diagonales están en el interior del polígono.
• Un polígono es cóncavo si no es convexo

Teselados regulares

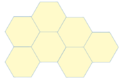
Los únicos polígonos regulares que cubren completamente una superficie plana son: el triángulo equilátero, el cuadrado y el hexágono.

Como la unión en cada vértice debe sumar 360º para que no queden espacios, los únicos polígonos regulares que suman 360 al unirlos por sus ángulos, interiores son estos tres.

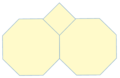
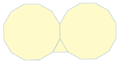
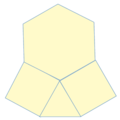
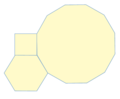
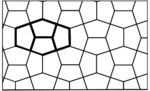
Teselados semiregulares

Son aquellos que contienen 2 o más polígonos regulares en su formación. Un teselado semiregular tiene las siguientes propiedades:

1. Está formada sólo por polígonos regulares.
2. El arreglo de polígonos es idéntico en cada vértice.
3. Existen sólo 8 teselados semi-regulares y poligonos verdes

Teselados con figuras semi-regulares

Teselados no regulares

Son aquellos formados por polígonos no regulares

Cuadriláteros

Cualquier paralelogramo tesela, ya que solo debemos prolongar sus lados paralelos y construir los nuevos paralelogramos congruentes al primero.

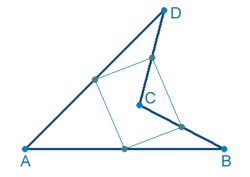
Con cualquier cuadrilátero, ya sea cóncavo o convexo, es posible cubrir una superficie plana. En el caso cóncavo es fácil de demostrar por el Teorema de Varignon, que los puntos medios de todo cuadrilátero forman un paralelogramo y luego Tesela. Este método se llama Método de la Malla Invisible

Triángulos

Con un triángulo escaleno es posible cubrir todo el plano. Esto se verifica formando el paralelogramo correspondiente.

Hexágonos

Además de los hexágonos regulares, los hexágonos no regulares con simetría central también teselan el plano. Otros hexágonos no regulares no teselan el plano.

Teselado de El Cairo

Teselado de El Cairo

Este teselado aparece frecuentemente en las calles de El Cairo, Egipto y en el arte islámico, de ahí su nombre.

Este pentágono posee dos ángulos rectos, un ángulo de 144° y dos ángulos de 108°.Como para todo pentágono, la suma de sus ángulos es de 540°.

Polígonos Cóncavos

Construcción de teselados

Método quita y pon

Consiste en dibujar una figura geométrica que por si sola tesele el plano, como un paralelogramo o un triángulo. Luego, se le van sacando partes de un lado, para luego ponerlas en el lado contrario. Luego se repite esta imagen en veces y se van colocando de modo que encajen perfectamente, utilizando las transformaciones isométricas (traslación, rotación y simetría). Escher se hizo famoso por sus cuadros de teselados construidos con este método.

Teselados e isometría

A partir de los movimientos o transformaciones en el plano se pueden lograr diversos diseños.

Véase también

• Maurits Cornelis Escher
• Polígonos de Thiessen
• Teselado de El Cairo
• Teselación de Penrose
• Transformaciones isométricas

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre TeseladoCommons.
• Sitio Oficial de Escher
• 14 Pentágonos que teselan el plano
• Video de teselados
• Diccionario de la Real Academia Española