Base de Hamel

Base de Hamel

Base de Hamel

Una Base de Hamel H de un espacio vectorial X sobre un cuerpo 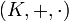(K,+,\cdot) consiste en un subconjunto de X que cumple:

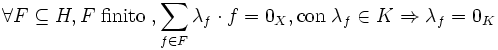
1)Es linealmente independiente: \forall F \subseteq H ,F \;\mathrm{finito}\;, \sum_{f\in F} \lambda_f \cdot f = 0_{X}, \mathrm{con} \;\lambda_{f} \in K \Rightarrow \lambda_f = 0_{K}

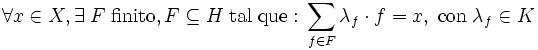
2)Genera X, es decir: \forall x \in X, \exist\; F \;\mathrm{finito}, F\subseteq H \; \mathrm{tal\; que:}\; \sum_{f\in F}\lambda_f \cdot f=x, \; \mathrm{con}\;\lambda_{f} \in K

Es posible demostrar en base al Axioma de Elección (o más directamente, en base a alguna de sus formas equivalentes como el Lema de Zorn o el Principio maximal de Hausdorff), que todo espacio vectorial admite una Base de Hamel.

Como ejemplo interesante podemos considerar a los números reales generados como espacio vectorial sobre los racionales. Se puede afirmar entonces que existe un 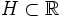H \subset \mathbb{R},la base de Hamel, tal que cualquier otro real puede ser escrito en forma única como una combinación lineal finita de racionales, con elementos de dicha base.

Temas relacionados

Base (álgebra)

Obtenido de "Base de Hamel"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Base (álgebra) — Saltar a navegación, búsqueda En álgebra lineal, se dice que un conjunto ordenado B es base de un espacio vectorial V si se cumplen las siguientes condiciones: Todos los elementos de la base B deben ser linealmente independientes. Todos los… …   Wikipedia Español

  • Hamel (Nord) — Pour les articles homonymes, voir Hamel. 50° 16′ 51″ N 3° 04′ 29″ E …   Wikipédia en Français

  • Georg Hamel — Georg Karl Wilhelm Hamel (né le 12 septembre 1877 à Düren; † 4 octobre 1954 à Landshut) est un mathématicien allemand. Il prouva dans un cas particulier, mais via une méthode générale, l existence d une base pour un espace vectoriel de dimension… …   Wikipédia en Français

  • Beaumont-Hamel Newfoundland Memorial — Veterans Affairs Canada Commonwealth War Graves Commission …   Wikipedia

  • Dreuil-hamel — est une ancienne commune française (dans le département de la Somme) aujourd hui intégrée à celle d Airaines. Par arrêté du 26 septembre 1972 (Journal officiel du 3 janvier 1973) avec effet au 1er octobre 1972, Dreuil Hamel est rattachée à… …   Wikipédia en Français

  • Dreuil-Hamel — est une ancienne commune française (dans le département de la Somme) aujourd hui intégrée à celle d Airaines. Par arrêté du 26 septembre 1972 (Journal officiel du 3 janvier 1973) avec effet au 1er octobre 1972, Dreuil Hamel est rattachée à… …   Wikipédia en Français

  • Le Hamel (Oise) — Pour les articles homonymes, voir Le Hamel. 49° 38′ 53″ N 1° 59′ 34″ E …   Wikipédia en Français

  • Théorème de la base incomplète — En algèbre linéaire, le théorème de la base incomplète affirme que, dans un espace vectoriel E, toute famille libre de vecteurs peut être complétée en une famille libre et génératrice de E (c est à dire une base de E) ; de toute famille… …   Wikipédia en Français

  • Beaumont-Hamel — Pour les articles homonymes, voir Beaumont et Hamel. 50° 05′ 04″ N 2° 39′ 26″ E …   Wikipédia en Français

  • Denis Hamel — Denis Hamel. Données clés Nationalité …   Wikipédia en Français

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”