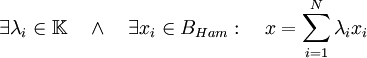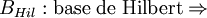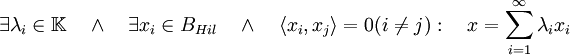Base (álgebra)

Base (álgebra)

Base (álgebra)

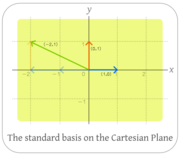
Basis graph.png

En álgebra lineal, se dice que un conjunto ordenado B es base de un espacio vectorial V si se cumplen las siguientes condiciones:

  • Todos los elementos de la base B deben ser linealmente independientes.
  • Todos los elementos de la base B deben pertenecer al espacio vectorial V.
  • Todo elemento de V se tiene que poder escribir de manera única como una combinación lineal de los elementos de la base B. De existir múltiples combinaciones de B para un mismo elemento, obtendríamos un sistema generador de V y se perdería el concepto de base (unicidad de cada combinación). Esta última premisa se desprende de la independencia lineal de la base.


Contenido

Bases de Hamel y de Hilbert

En un espacio vectorial de Hilbert de dimensión infinita existen varias posibilidades de extender el concepto de combinación lineal finita. De un lado si consideramos únicamente combinaciones lineales finitas llegamos al concepto de base de Hamel o base lineal. Puede probarse que todas las bases de Hamel tienen el mismo número de elementos, este número o cardinal se llama dimensión lineal o dimensión de Hamel. Un conjunto constituye una base de Hamel si y solo si:

B_{Ham}:\mbox{base de Hamel} \Rightarrow
\exists \lambda_i \in \mathbb{K} \quad \and \quad \exists x_i \in B_{Ham}: \quad x = \sum_{i=1}^N \lambda_i x_i


En un espacio de dimensión de Hamel finita, se puede encontrar solamente un número finito de vectores ortogonales dos a dos, en cambio, cuando la dimensión de Hamel es infinita, pueden introducirse en los espacios de Hilbert ciertas "combinaciones lineales infinitas" en términos de vectores ortogonales. En un espacio de Hilbert de dimensión infinita se dice que un conjunto es una base de Hilbert o base ortogonal, si y solo si:

B_{Hil}:\mbox{base de Hilbert} \Rightarrow
\exists \lambda_i \in \mathbb{K} \quad \and \quad \exists x_i \in B_{Hil} \quad \and \quad \langle x_i,x_j \rangle = 0 (i \ne j): \quad x = \sum_{i=1}^\infty \lambda_i x_i


Nuevamente sucede que todas las bases ortogonales tienen el mismo cardinal, por lo que se define el concepto de dimensión de Hilbert como el cardinal de cualquier base de Hilbert.

Dimensión vectorial

Vecteur bases ond et qcq.png

La dimensión de un espacio vectorial se define como el número de elementos o cardinal de una base de dicho espacio. Dado que para todo espacio de Hilbert de dimensión infinita podemos distinguir entre bases de Hilbert y de Hamel, podemos definir la dimensión vectorial ordinaria y la dimensión vectorial de Hilbert. Se tiene que para cualquier espacio vectorial V, la relación entre dimensión de Hammel y dimensión de Hilbert es la siguiente:

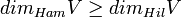
(1) dim_{Ham} V \ge dim_{Hil} V

En espacios de dimensión finita también se pueden definir las bases de Hilbert como bases de Hamel ortogonales. De hecho, para un espacio de dimensión finita, la dimensión de Hilbert es igual a la dimensión de Hamel. En dimensión finita toda base de Hamel es base de Hilbert y viceversa, por lo que para un espacio de dimensión finita en (1) se da siempre la igualdad.

Observaciones adicionales

1) Las bases son conjuntos ordenados. Es decir que si bien {a,b,c} y {b,a,c} generan el mismo espacio vectorial, las bases no son iguales.

2) De la observación anterior se desprende que las bases no son únicas. En general, suele haber infinitas bases distintas para un mismo espacio vectorial. Por ejemplo, si 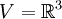V=\mathbb{R}^3, una posible base de V es: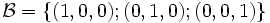

\mathcal{B}=\{ (1,0,0); (0,1,0); (0,0,1)\}

Pero otras posibles bases de V son:

\begin{cases} \mathcal{B}'=\{(2,0,0); (0,1,0); (0,0,1)\} \\ \mathcal{B}''=\{(1,1,1); (1,1,0); (1,0,0)\} \\ \mathcal{B}'''=\{(504,0,0); (0,7,0); (0,0,1/2)\} \end{cases}

En general, una base cualquiera estará formada por tres vectores linealmente independientes que pertenezcan a 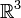\mathbb{R}^3. Cuando el espacio vectorial en sí mismo es un conjunto finito entonces necesariamente existe un número finito de bases.

3) Si V es un espacio vectorial de dimensión finita, entonces todas las bases de V serán finitas y tendrán la misma cantidad de elementos.

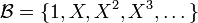
4) No todas las bases tienen un número finito de elementos. Por ejemplo, las bases del espacio vectorial de los polinomios de una variable tienen infinitos elementos. Una posible base es la formada por las potencias de X: \mathcal{B} =\{1, X, X^2, X^3,\dots \}

Temas relacionados

Véase también

  • Método de ortogonalización de Gram-Schmidt
Obtenido de "Base (%C3%A1lgebra)"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Base (álgebra) — En álgebra lineal, se denomina base de un espacio vectorial de dimensión finita a todo sistema generador libre (linealmente independiente) de dicho espacio vectorial. Dado un espacio vectorial de dimensión finita V, para que un sistema o conjunto …   Enciclopedia Universal

  • Base de Hamel — Saltar a navegación, búsqueda Una Base de Hamel H de un espacio vectorial X sobre un cuerpo consiste en un subconjunto de X que cumple: 1)Es linealmente independiente: 2)Genera X, es decir …   Wikipedia Español

  • Álgebra lineal — El álgebra lineal es la rama de las matemáticas que estudia conceptos tales como vectores, matrices, sistemas de ecuaciones lineales y en un enfoque más formal, espacios vectoriales, y sus transformaciones lineales. Es un área activa que tiene… …   Wikipedia Español

  • Base de datos espacial — Saltar a navegación, búsqueda Base de datos espacial (spatial database) es un sistema administrador de bases de datos que maneja datos existentes en un espacio o datos espaciales. En este tipo de bases de datos es imprescindible establecer un… …   Wikipedia Español

  • Base ortonormal — Saltar a navegación, búsqueda En álgebra lineal, una base ortonormal de un espacio prehilbertiano V (es decir, un espacio vectorial con producto interno) o, en particular, de un espacio de Hilbert H, es un conjunto de elementos cuyo span es denso …   Wikipedia Español

  • Base dual — Saltar a navegación, búsqueda En álgebra lineal, una base dual o base biortogonal es un conjunto de vectores que forman una base para el espacio dual de un espacio vectorial. Para un espacio vectorial V de dimensiones finitas, el espacio dual V*… …   Wikipedia Español

  • Base de datos relacional — Saltar a navegación, búsqueda Una base de datos relacional es una base de datos que cumple con el modelo relacional, el cual es el modelo más utilizado en la actualidad para modelar problemas reales y administrar datos dinámicamente. Permiten… …   Wikipedia Español

  • Base De Gröbner — Une base de Gröbner (ou base standard, ou base de Buchberger) d un idéal I de l anneau de polynômes est un ensemble de générateurs de cet idéal, vérifiant certaines propriétés supplémentaires. Cette notion a été introduite dans les années 1960,… …   Wikipédia en Français

  • Base de Grobner — Base de Gröbner Une base de Gröbner (ou base standard, ou base de Buchberger) d un idéal I de l anneau de polynômes est un ensemble de générateurs de cet idéal, vérifiant certaines propriétés supplémentaires. Cette notion a été introduite dans… …   Wikipédia en Français

  • Base de gröbner — Une base de Gröbner (ou base standard, ou base de Buchberger) d un idéal I de l anneau de polynômes est un ensemble de générateurs de cet idéal, vérifiant certaines propriétés supplémentaires. Cette notion a été introduite dans les années 1960,… …   Wikipédia en Français

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”