- Bien definido
-
Bien definido
En matemáticas, el término bien definido se usa para especificar que un concepto (una función, una propiedad, una relación, etc.) se define de forma lógica o matemática usando un conjunto de axiomas básicos sin ambigüedad alguna. Usualmente las definiciones se enuncian sin ambigüedad, y no hay preguntas acerca de su buena definición. Ocasionalmente, sin embargo, se enuncia una definición por una elección arbitraria por motivos de economía; entonces uno debe comprobar que la definición es independiente de dicha elección.
Una de las situaciones más comunes en matemáticas es aquella en que el término "bien definido" se usa al tratar con clases laterales en la teoría de grupos. Es tan importante verificar que se obtenga el mismo resultado independientemente de que representante de la clase lateral se elija como lo es que se obtenga siempre el mismo resultado cuando se practican operaciones aritméticas (por ejemplo, nunca sucede que
).Más generalmente, dado un conjunto X, una relación de equivalencia ~ en X, y una función f en X, uno puede estar interesado en saber si f puede ser vista como una función en el conjunto de cocientes X/~. Es decir, si [x] es una clase de equivalencia en X/~, entonces uno puede intentar definir f([x]) = f(x). Si la función satisface f(x) = f(y) cuando x~y, entonces la definición tiene sentido, y f está bien definida en X/~. Aunque la distinción frecuentemente se ignore, la función en X/~, teniendo un dominio diferente, debería ser vista como un mapeo distinto
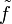. Visto de esta forma, uno dice que 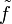está bien definida si el diagrama mostrado conmuta. Esto es, que f se factoriza a través de π, donde π es el mapeo de proyección canónica X → X/~, tal que 
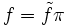.El concepto de buena definición es importante para las matemáticas y ciencias para no tener que depender de la intuición humana, la cual es subjetiva e imprecisa. Por ejemplo, podría decirse que un objeto puede tener la propiedad de ser "rojo"; sin embargo, esta propiedad no está definida porque hay una amplia variedad de colores que algunos individuos percibirían como un tono de rojo, cuando otros insistirían que es naranja. Tal propiedad solamente estaría bien definida si reglas estrictas determinaran cuales frecuencias de luz visible el objeto estuviera permitido para emitir o reflejar para que sea "rojo".
Otro ejemplo sería que la mayoría de la gente aceptaría que 999 es casi tanto como 1000. Sin embargo, no hay una frontera clara que marque donde casi tanto como' comienza o termina (hay, sin embargo, una noción bien definida de conjuntos infinitos que son casi otros).
Categoría: Miscelánea matemática
Wikimedia foundation. 2010.
