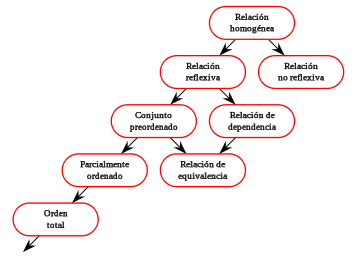
Relación de equivalencia

Relación de equivalencia
Relación homogénea Relación reflexiva Relación no reflexiva Conjunto preordenado Relación de dependencia Conjunto parcialmente ordenado Relación de equivalencia Orden totalClasiBinaEs 004.svg
Acerca de esta imagen


Sea K un conjunto dado no vacío y R una relación binaria definida sobre K. Se dice que R es una relación de equivalencia si cumple las siguientes propiedades:

  • Reflexividad: Todo elemento de K está relacionado consigo mismo. Es decir,
\forall x\in K, \; xRx.
  • Simetría: Si un elemento de K está relacionado con otro, entonces ese otro elemento también se relaciona con el primero. Es decir,
\forall x,y\in K, \; xRy \; \Rightarrow \; yRx
  • Transitividad: Si un elemento de K está relacionado con otro, y ese otro a su vez se relaciona con un tercero, entonces el primero estará relacionado también con este último. Es decir,
\forall x,y,z\in K, \; xRy , yRz \; \Rightarrow \; xRz

Una relación de equivalencia R sobre un conjunto K puede denotarse con el par ordenado (K,\sim)\,.

Contenido

Clases de equivalencia

La relación de equivalencia ∼ define subconjuntos disjuntos en K llamados clases de equivalencia de la siguiente manera: Dado un elemento a\in K, al conjunto dado por todos los elementos relacionados con a

[a] = \{b\in K\,|\,b\sim a\}

se le llama la clase de equivalencia asociada al elemento a. Al elemento a se le llama representante de la clase.

Se llama orden al número de clases que genera una relación de equivalencia; si éste es finito, se dice que la relación es de orden finito.

El concepto de clase de equivalencia tiene importancia en ciencia, dado un conjunto de objetos o entidades abstractas (potencialmente infinitas), pueden establecerse relaciones de equivalencia en base a algún criterio, las clases resultantes son los "tipos" en los que se puede clasificar toda la gama de objetos.

Conjunto cociente

El conjunto de todas las clases de equivalencia se denomina conjunto cociente y se lo suele denotar como:

K/\sim\, \qquad \qquad K/\sim = \{[a]\in \mathcal{P}(K)|\ ([a]\cap[b]\ne 0) \iff \left( \exists a\in [a] \land \iff \exists b\in [b]: a\sim b \right) \}

Tal como muestra la definición anterior el conjunto cociente es un subconjunto del conjunto de partes de K.

Lema de abstracción

Help-books-aj.svg aj ash 01.svg
 Este artículo o sección tiene un estilo difícil de entender para los lectores interesados en el tema.
Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a los especialistas.

Este conjunto es una partición de K, es decir: K está formado por el conjunto de todas las clases de equivalencia {a} de la relación, que son conjuntos disjuntos entre sí (es decir, no se superponen):

  1. para cualquiera dos ai,aj no relacionados tenemos: [a_i]\cap[a_j]=\emptyset;
  2. la unión de todos integra al total: \bigcup_s[a_s]=K

Esto es: las clases de equivalencia no tienen elementos en común y la unión de todas ellas rellena K, es igual al conjunto K completo.

Lo reciproco también es cierto: Dada una partición de un conjunto existe una relación de equivalencia en él de tal manera que las clases de equivalencia coinciden con los componentes de la partición

Las ideas enunciadas en los dos párrafos previos constituyen el lema denominado como Lema de abstracción, pilar de entrada al método abstracto matemático.

Es también conocido con el calificativo teorema fundamental de las relaciones de equivalencia

El conjunto cociente se representa: A/R={A1,A2,A3....An}

Ejemplos

  • La igualdad entre los elementos de un conjunto.
  • La relación de congruencia módulo M en el conjunto de los números enteros (i.e. M\in\mathbb{Z}), donde se define: a∼b si y sólo si a - b\, es múltiplo de M.
Esta relación es de equivalencia porque:
  • Es reflexiva: a - a = 0, que es múltiplo de M.
  • Es simétrica: si a - b es múltiplo de M, entonces b - a = -(a - b) también es múltiplo de M.
  • Es transitiva: sean k y l números enteros tales que a - b = M k y b - c = M l. Entonces, a - c = (a - b) + (b - c) = M k + M l = M(k + l) y por tanto un múltiplo de M. En particular, si M = 2 tenemos la tradicional clasificación de los números enteros en pares e impares.
  • Sea H un subgrupo de un grupo G. Definiendo para elementos del grupo a∼b si y sólo si ab^{-1}\in H, tendremos la relación de equivalencia llamada congruencia módulo H .
  • Definiendo, para elementos del grupo, a∼b si y sólo si existe g en G talque gag − 1 = b, se llama relación de conjugación. Sus clases: clases de conjugación. Las clases de equivalencia reciben el nombre de órbita o clase de conjugación.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Relación de equivalencia — Una relación de equivalencia sobre K es una relación binaria Relación de equivalencia que cumple las siguientes propiedades: ● Es reflexiva: ∀a ∈ K, a Relación de equivalencia a. ● Es simétrica: a Relación de equivalencia b ⇒ b Relación de equiva …   Enciclopedia Universal

  • Relación binaria — Saltar a navegación, búsqueda En matemáticas, una relación binaria es una relación matemática R entre los elementos de dos conjuntos A y B. Una relación de este tipo se puede representar mediante pares ordenados, : Las dos propo …   Wikipedia Español

  • Relación matemática — Saltar a navegación, búsqueda Una relación , de los conjuntos es un subconjunto del producto cartesiano Una Relación binaria es una relación entre dos conjuntos. El concepto de relación implica la idea de enumeración, de algunos de los elementos …   Wikipedia Español

  • equivalencia — ► sustantivo femenino Igualdad en el valor, eficacia o potencia de varias cosas. * * * equivalencia f. Cualidad de equivalente. ⊚ Relación entre cosas equivalentes. ⃞ Formas de expresión Se expresa la equivalencia con «por»: ‘Teníamos un montón… …   Enciclopedia Universal

  • Equivalencia estática — La acción de una fuerza desplazada sobre una llave inglesa, es estáticamente equivalente a una fuerza y un momento aplicados sobre el centro geométrico de la tuerca. La equivalencia estática es una relación de equivalencia entre sistemas de… …   Wikipedia Español

  • Relación — (Del lat. relatio, onis.) ► sustantivo femenino 1 Situación entre dos cosa, ideas o hechos unidos por alguna circunstancia, en la realidad o en la mente de una persona: ■ la policía asegura que este robo no tiene relación con el anterior; su… …   Enciclopedia Universal

  • Equivalencia entre masa y energía — «E=MC²» redirige aquí. Para otras acepciones, véase E=MC² (desambiguación). Escultura de la ecuación en el Paseo de las Ideas, Alemania. La equivalencia entre la masa y la energía dada por la expresión de la teoría de la relatividad de Einstein …   Wikipedia Español

  • equivalencia — s f Relación de igualdad entre cada uno de los elementos, partes, propiedades o funciones de dos o más cosas: equivalencia de conjuntos, una equivalencia monetaria …   Español en México

  • Clase de equivalencia — En matemáticas; sea Clase de equivalencia una relación de equivalencia y K el conjunto sobre el que está definida, llamaremos clase de equivalencia del elemento a ∈ K, al subconjunto [a]Clase de equivalencia de K formado por todos los elementos… …   Enciclopedia Universal

  • Aritmética modular — Saltar a navegación, búsqueda Cubierta de la edición original de Disquisitiones arithmeticae de Gauss, libro fundamental de la aritmética modular. En matemática, la aritmética modular es un sistema aritmético para clases de equivalencia((Clase de …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”