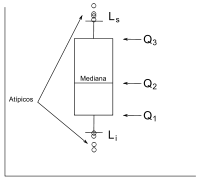
Diagrama de caja

Diagrama de caja

Diagrama de caja

Diagrama de caja (Box-Plot)

Un diagrama de caja es un gráfico, basado en cuartiles, mediante el cual se visualiza un conjunto de datos. Está compuesto por un rectángulo, la "caja", y dos brazos, los "bigotes".

Es un gráfico que suministra información sobre los valores mínimo y máximo, los cuartiles Q1, Q2 o mediana y Q3, y sobre la existencia de valores atípicos y la simetría de la distribución.

Cómo dibujarlo

                            +-----+-+    
  *           o     |-------|     | |---|
                            +-----+-+    
                                         
+---+---+---+---+---+---+---+---+---+---+---+---+
0   1   2   3   4   5   6   7   8   9  10  11  12
  • Ordenar los datos y obtener el valor mínimo, el máximo, los cuartiles Q1, Q2 y Q3 y el intervalo intercuartil (IQR)
En el ejemplo:
  • Valor 7: es el Q1 (25% de los datos)
  • Valor 8.5: es el Q2 o mediana (el 50% de los datos)
  • Valor 9: es el Q3 (75% de los datos)
  • Intervalo intercuartil IQR (Q3-Q1)=2
  • Dibujar un rectángulo con Q1 y Q3 como extremos e indicar la posición de la mediana (Q2) mediante una línea.
  • Para dibujar los bigotes, las líneas que se extienden desde la caja, hay que calcular los límites superior e inferior, Li y Ls, que identifiquen a los valores atípicos.
Para ello se calcula cuándo se consideran atípicos los valores. Son aquellos inferiores a Q1-1.5*IQR o superiores a Q3+1.5*IQR.
En el ejemplo:
  • inferior: 7-1.5*2=4
  • superior: 9+1.5*2=12
Ahora se buscan los últimos valores que NO son atípicos, que serán los extremos de los bigotes.
  • En el ejemplo: 5 y 10
  • Marcar como atípicos todos los datos que están fuera del intervalo (Li, Ls).
En el ejemplo: 0.5 y 3.5
  • Además, se pueden considerar valores extremadamente atípicos aquellos que exceden Q1-3*IQR o Q3+3*IQR.
De modo que, en el ejemplo:
  • inferior: 7-3*2=1
  • superior: 9+3*2=15
El valor 0.5 seria atípico extremo y el 3.5 sería atípico

Utilidad

  • Proporcionan una visión general de la simetría de la distribución de los datos; si la mediana no está en el centro del rectángulo, la distribución no es simétrica.
  • Son útiles para ver la presencia de valores atípicos.

Enlaces externos

CiberConta

Obtenido de "Diagrama de caja"

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Diagrama de despliegue — Saltar a navegación, búsqueda Un ejemplo de diagrama de despliegue. El Diagrama de Despliegue es un tipo de diagrama del Lenguaje Unificado de Modelado que se utiliza para modelar el hardware utilizado en las implementaciones de sistemas y las… …   Wikipedia Español

  • Parámetro estadístico — Saltar a navegación, búsqueda La media aritmética …   Wikipedia Español

  • Calest — Saltar a navegación, búsqueda CalEst Archivo:CalEst.jpg Entorno de CalEst Desarrollador Conteck www.calest.org …   Wikipedia Español

  • Medidas de posición no central — Los cuantiles 0.25, 0.50 y 0.75 de la distribución normal. Más conocidos como los cuartiles Q 1, Q 2 y Q 3, dividen la distribución en cuatro bloques, cada uno de los cuales contiene el 25% de los datos. En estadística descriptiva, las medidas de …   Wikipedia Español

  • Valor atípico — En las estadísticas, tales como muestras estratificadas, un valor atípico es una observación que es numéricamente distante del resto de los datos. Las estadísticas derivadas de los conjuntos de datos que incluyen valores atípicos serán… …   Wikipedia Español

  • Campo de béisbol — Diagrama de un campo de béisbol (la parte interior, comprendida entre las bases, ocasionalmente se menciona como diamante ) …   Wikipedia Español

  • Centrómero — Diagrama de un cromosoma eucariótico duplicado y condensado (en metafase mitótica). (1) Cromátida, cada una de las partes idénticas de un cromosoma luego de la duplicación del ADN. (2) Centrómero, el lugar del cromosoma en el cual ambas… …   Wikipedia Español

  • Efecto Hall — Diagrama del efecto Hall, mostrando el flujo de electrones. (en vez de la corriente convencional). Leyenda: 1. Electrones 2. Sensor o sonda Hall 3. Imanes 4. Campo magnético 5. Fuente de energía Descripción En la imagen A, una carga negativa… …   Wikipedia Español

  • Trasplante de corazón — Diagrama ilustrando la colocación de un corazón donado por el procedimiento de trasplante cardíaco ortotópico. Trasplante de corazón, es un tipo de operación quirúrgica de trasplante de órgano realizado sobre pacientes en estado de insuficiencia… …   Wikipedia Español

  • Máquina de estados algorítmica — La Máquina de estados algorítmica (ASM) es un método para el diseño de Máquina de estados finitos. Se utiliza para representar los diagramas de circuito integrado s digitales. El diagrama de ASM es como un diagrama de estado, pero menos formal y… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”