Medidas de posición no central

Los cuantiles 0.25, 0.50 y 0.75 de la distribución normal. Más conocidos como los cuartiles Q_1, Q_2 y Q_3, dividen la distribución en cuatro bloques, cada uno de los cuales contiene el 25% de los datos.

En estadística descriptiva, las medidas de posición no central permiten conocer otros puntos característicos de la distribución que no son los valores centrales. Entre las medidas de posición no central más importantes están los cuantiles.

El término cuantil fue usado por primera vez por Kendall en 1940. El cuantil de orden p de una distribución (con 0 < p < 1) es el valor de la variable x_p que marca un corte de modo que una proporción p de valores de la población es menor o igual que x_p. Por ejemplo, el cuantil de orden 0.36 dejaría un 36% de valores por debajo y el cuantil de orden 0.50 se corresponde con la mediana de la distribución.

Los cuantiles suelen usarse por grupos que dividen la distribución en partes iguales; entendidas estas como intervalos que comprenden la misma proporción de valores. Los más usados son:

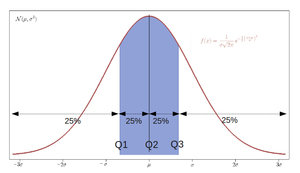
• Los Cuartiles, que dividen a la distribución en cuatro partes (corresponden a los cuantiles 0.25, 0.50 y 0.75);
• Los Quintiles, que dividen a la distribución en cinco partes (corresponden a los cuantiles 0.20, 0.40, 0.60 y 0.80) ;
• Los Deciles, que dividen a la distribución en diez partes;
• Los Percentiles, que dividen a la distribución en cien partes.

En el cálculo de cuantiles con distribuciones de variable continua (por ejemplo, con datos agrupados) puede conseguirse fácilmente que las partes en que se divide la distribución sean exactamente iguales. Sin embargo, en las distribuciones de variable discreta (como el caso de datos aislados) debemos conformarnos con que estas partes sean aproximadamente iguales. Por desgracia, no hay consenso sobre la forma en que realizar esta aproximación, existiendo en la literatura científica nueve métodos diferentes, que conducen a resultados diferentes. Por ello, al calcular cualquier cuantil de datos no agrupados por medio de calculadora, software o manualmente, es básico el saber e indicar el método utilizado.

La función que a cada p le asigna el punto de corte x_p, es decir, el valor del cuantil de orden p, se denomina función cuantil.

Cálculo de cuantiles de datos agrupados en intervalos

Calcularemos el cuantil de orden 0.30 de la edad de la población de una aldea resumida en la tabla:

Edad de la población	habitantes	frecuencia acumulada
0-20	9	9
20-40	18	27
40-60	26	53
60-80	7	60
80-100	4	64

Nuestro primer paso será hallar el intervalo en que se encuentra nuestro cuantil: De un total de 64 datos, el cuantil 0.30 ocupará la posición np=64×0.3=19.2. Observamos en la columna de frecuencias acumuladas que este valor, por estar comprendido entre 18 y 27, corresponde al intervalo 20-40.

Dentro de este intervalo, seleccionaremos el valor de nuestro cuantil por simple interpolación lineal. Para ello, siguiendo las indicaciones del gráfico, sólo será necesario hacer una regla de tres.

Observamos en la figura dos triángulos semejantes: OAB y OCD. El cuantil buscado corresponderá a la abscisa 20+x. Razonando por semejanza, OB=x es a AB=10.2, como OD=20 es a CD=18. Despejando obtenemos x=11.33, luego el cuantil buscado es a 20+x=31.33.

Cuantiles destacados

Cuartiles

Los cuartiles son los tres valores que dividen al conjunto de datos ordenados en cuatro partes porcentualmente iguales. Aparecen citados en la literatura científica por primera vez en 1879 por D. McAlister.^[1]

La diferencia entre el tercer cuartil y el primero se conoce como rango intercuartílico. Se representa gráficamente como la anchura de las cajas en los llamados diagramas de cajas.

Dada una serie de valores X₁,X₂,X₃ ...X_n ordenados en forma creciente, podemos pensar que su cálculo podría efectuarse:

• Primer cuartil (Q₁) como la mediana de la primera mitad de valores;
• Segundo cuartil (Q₂) como la propia mediana de la serie;
• Tercer cuartil (Q₃) como la mediana de la segunda mitad de valores.

Pero esto conduce a distintos métodos de cálculo de los cuartiles primero (resp. tercero) según la propia mediana se incluya o excluya en la serie de la primera (resp. segunda) mitad de valores.

Cálculo con datos no Agrupados

No hay uniformidad sobre su cálculo. en la bibliografía se encuentran hasta cinco métodos que dan resultados diferentes.^[2] Uno de los métodos es el siguiente: dados n datos ordenados,

• El primer cuartil:

(n+3)/4

• Para el tercer cuartil

(3n+1)/4

Percentiles

Se representan con la letra P. Para el percentil i-ésimo, donde la i toma valores del 1 al 99. El i % de la muestra son valores menores que él y el 100-i % restante son mayores.

Aparecen citados en la literatura científica por primera vez por Francis Galton en 1885^[3]

• P₂₅ = Q₁.
• P₅₀ = Q₂ = mediana.
• P₇₅ = Q₃.

Cálculo con datos no Agrupados

Un método para calcular un percentil sería el siguiente: Calculamos donde n es el número de elementos de la muestra e i el percentil. El resultado de realizar esta operación da como resultado un número real con parte entera E y parte decimal D. Teniendo en cuenta estos 2 valores, aplicamos la siguiente función:

El resultado de esta última operación es el valor del percentil pedido.

Cálculos con ordenador

Con paquetes de software estadístico

Hay varios métodos, que conducen a resultados distintos, para estimar el valor de los cuantiles.^[4] La batería completa de nueve métodos está disponible en el lenguaje de programación R;^[5] SAS incluye cinco de los métodos citados; STAT, cuatro. A diferencia de estos, software de propósito general como Microsoft Excel incluye sólo uno de los métodos.

Con software matemático de propósito general

Citaremos en este caso el uso de Scilab, Matlab y Excel.

Percentiles

En Scilab, los percentiles de un conjunto de datos son calculados con la instrucción “perctl”. A esta instrucción hay que introducirle dos vectores. Uno de ellos “x” debe contener los datos que queremos procesar y en el otro “y”, valores enteros comprendidos entre el 1 y el 100. La función calcula cuales son los valores de “x” que se corresponden con los percentiles indicados en “y”. Por ejemplo:

x=[7,12,4,8,3,10,11,5,13,1,12,3,5,1,17,4,8,8,7,19,8,1,7,17,4,7,1,7,3,7,3,13,3,4,7,8,10,2,5,11,5,4,3,5,8];
y=[15,25,60,80]

calcularía los percentiles 15, 25, 60 y 80 del conjunto de datos del vector “x”, mostrando en la salida una matriz de dos columnas. En la primera de ellas aparecen los valores de los percentiles pedidos y en la segunda aparece la posición que ocupan en el vector “x” dichos valores:

prctile(x,y)
ans  =
   3.     43.
   4.      3.
   7.     media de los elementos 1 y 19.
  10.5    media de los elementos 6 y 7

Cuartiles

Siguiendo con Scilab, los cuartiles de la muestra son calculados con la instrucción “quart”. Esta instrucción es más sencilla que la anterior. Basta con introducirle un vector o matriz de valores y nos devolverá un vector con el valor de los cuartiles de los datos introducidos. Scilab también nos permite calcular el rango intercuartilico que es la distancia que hay entre un cuartil y otro. Podemos hacerlo con la instrucción “iqr”. Voy a usar el mismo vector “x” que en el caso anterior:

quart(x)
ans  =   3.75   7.    8.5
iqr(x)
ans  =  4.75

Para MSExcel se puede usar

=cuartil(RANGO, 1)

=cuartil(RANGO, 2)

=cuartil(RANGO, 3)

donde RANGO son los datos de los cuales queremos extraer el cuartil y el valor 1, 2 y 3 indican el primer, segunto y tercer cuartil.

Referencias

Véase también

• Diagrama de caja para la representación gráfica de los cuartiles.
• Función cuantil
• Medidas de tendencia central
• Rango intercuartil