Contenido 1 Introducción a las búsquedas no informadas 2 Representación del espacio de estados 3 La búsqueda en profundidad 4 La búsqueda en anchura 5 Véase también 6 Enlaces externos

Introducción a las búsquedas no informadas

Un problema típico de la Inteligencia Artificial consiste en buscar un estado concreto entre un conjunto determinado, al que se le llama espacio de estados. Imaginemos, por ejemplo, una habitación con baldosines en la que hay un libro. Un robot se desea desplazar por la habitación con el fin de llegar a dicho libro. ¿De qué manera lo hará? En este punto es donde entran en juego las estrategias y los algoritmos de búsqueda.

Cuando el sistema agente (en este caso, el robot) posee algún tipo de información del medio, se utilizan técnicas de búsquedas informadas; sin embargo, si carece de conocimiento alguno, se deberán emplear algoritmos de búsqueda no informadas. En nuestro ejemplo, y para este último caso, podemos imaginar un robot que no posea ningún tipo de visión artificial, que únicamente sea capaz de moverse en horizontal o vertical de un baldosín a otro y detectar si en el baldosín se halla el libro.

Representación del espacio de estados

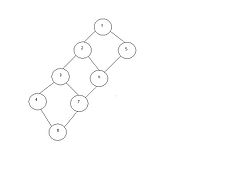
El conjunto de estados que el agente (en nuestro ejemplo, el robot) debe recorrer, generalmente se representa mediante un grafo, aunque en algunos casos concretos utilizaremos árboles. Siguiendo con nuestro ejemplo, cada nodo del grafo representará a uno de los baldosines de la habitación, y dos nodos serán adyacentes si también lo son sus baldosines correspondientes.

El grafo del dibujo en la parte inferior representa el tablero de manera parcial, y cada nodo es identificado por un número. Suponemos que la posición inicial del robot es el baldosín marcado con el número 1. En este grafo se aplica una correspondencia entre los nodos del mismo y los baldosines numerados de igual forma. Como se puede observar en el tablero, por ejemplo, el baldosín 1 es adyacente al 2 y al 5, y este hecho queda plasmado en el dibujo mostrado.

La búsqueda en profundidad

Supongamos que nuestro robot no tiene ninguna capacidad especial para poder moverse por la habitación de una manera eficiente (desconoce cualquier información útil para poder llegar al libro de la forma más corta): entonces deberá seguir un algoritmo de búsqueda no informada (“un método ciego”) para llegar hasta él. En general, este tipo de algoritmos recorre el espacio de estados de una forma concreta hasta dar con el objetivo (en este caso, el libro). Nuestro primer método se denomina búsqueda en profundidad.

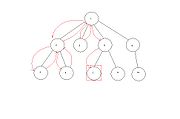
Supongamos el árbol del dibujo representando un espacio de estados cualquiera. Vemos que, teniendo este árbol delante con sus nodos numerados, tenemos distintas formas de recorrerlo. ¿Cómo lo hacemos en profundidad? Siendo el 1 el nodo inicial y 7 el nodo objetivo que se debe alcanzar, hacemos lo siguiente: buscaremos en todas las ramas que cuelgan, de izquierda a derecha, y exploramos cada rama hasta llegar a una hoja. Para cada hijo buscamos a su vez en profundidad, parando cuando se encuentre el objetivo. En este ejemplo, la secuencia a seguir está indicada por el número de los nodos: 1-> 2-> 3-> 4-> 5-> 6-> 7.

Si el camino tiene longitud k y factor de ramificación r, la complejidad espacial del algoritmo está en O (k+r). Su complejidad temporal depende tanto del factor de ramificación como de la profundidad de la solución. Siendo n el número medio de hijos expandidos, y si la solución se alcanza en el nivel p, la complejidad temporal está en O (n^p); es, por tanto, un coste exponencial.

Este algoritmo de búsqueda, además, no es completo, ya que si existe solución y se mete por una rama infinita puede que no termine nunca. Tampoco es óptimo, ya que puede encontrar la solución pero haciendo un recorrido mayor del necesario en general. Se ha usado una estructura pila LIFO para implementarlo.

halla_objetivo_profundidad (A: espacio_de_busquedas)

  { /* dev objetivo*/
     Pila lista_nodos;
     Boolean acabar = false;
     lista_nodos.apilar (A.nodo_raiz);
     while ((!lista_nodos.esVacia()) AND (!acabar)) do
     {
        nodo_actual = lista_nodos.cima(); 
        lista_nodos.desapila();
        if (esObjetivo (nodo_actual) ) then
           {
                acabar = true;
           }
        else
           {
                  nodo_actual.expandir(); //se añaden los hijos del nodo actual
 	           lista_nodos.apilarMuchos (nodos_expandidos_de_nodo_actual);
           }
     }
     return nodo_actual;
  }

---

La búsqueda en anchura

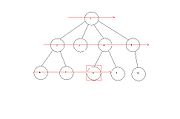
Otra opción para recorrer el espacio de estados sin conocer ninguna información acerca del mismo es recorrerlo en anchura. Como su nombre indica, el recorrido realizado se lleva a cabo visitando todos los nodos de un nivel, de izquierda a derecha, pasando posteriormente al nivel siguiente, hasta que se encuentre el nodo objetivo, momento en el que se detiene el algoritmo. Lo vemos en el dibujo con el mismo ejemplo de antes, numerando los nodos con el orden que les corresponde según el recorrido en anchura.

En efecto, los nodos que con este algoritmo se visitan hasta encontrar el objetivo (8) son: 1-> 2-> 3-> 4-> 5-> 6-> 7-> 8

Su complejidad tanto espacial como temporal es exponencial, y está en O (n^p), siendo n el número medio de sucesores, y p el nivel donde se alcanza la solución; por ello, esta estrategia es sólo aplicable a problemas no demasiado amplios.

Este procedimiento es completo, ya que encontrará siempre una solución si es que la hay, pero en general no es óptimo. Para implementarlo se ha hecho uso de una cola FIFO.

halla_objetivo_anchura (A: espacio_de_busquedas)

  { /* dev objetivo*/
     Cola lista_nodos;
     Boolean acabar = false;
     lista_nodos.encolar (A.nodo_raiz);
     while ((!lista_nodos.esVacia()) AND (!acabar)) do
     {
        nodo_actual = lista_nodos.primero(); 
        lista_nodos.quitaPrimero();
        if (esObjetivo (nodo_actual) ) then
           {
                acabar = true;
           }
        else
           {
                  nodo_actual.expandir(); //se añaden los hijos del nodo actual
 	           lista_nodos.encolarMuchos (nodos_expandidos_de_nodo_actual);
           }
     }
     return nodo_actual;
  }

---

Véase también

• Árbol (estructura de datos)
• Búsqueda en anchura
• Búsqueda en profundidad
• Inteligencia artificial
• Cola (estructura de datos)
• Pila (estructura de datos)

Enlaces externos

• Noticias sobre IA (en inglés)
• Asociación Española de IA
• Más sobre IA