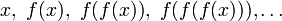En matemáticas, un punto fijo de una función es un punto cuya imagen por la función es él mismo. Es decir, x es un punto fijo de la función f si y sólo si f(x) = x. Por ejemplo, si f está definida sobre los números reales como

f(x) = x² − 3x + 4,~

entonces 2 es un punto fijo de f, porque f(2) = 2.

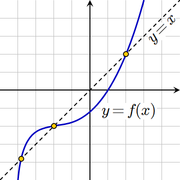
No todas las funciones tienen puntos fijos, por ejemplo, si f es una función definida sobre los números reales como f(x) = x + 1, entonces no tiene ningún punto fijo, ya que x no es nunca igual a x + 1 para ningún número real. En términos gráficos, un punto fijo significa que el punto (x,f(x)) pertenece a la recta y = x, o en otras palabras la gráfica de f tiene un punto en común con esa recta. El ejemplo f(x) = x + 1 es un caso donde la gráfico y la recta son un par de paralelas.

Los puntos que vuelven al mismo valor después de un número finito de iteraciones de la función se conocen como puntos periódicos; un punto fijo es un punto periódico con periodo igual a 1.

Contenido 1 Puntos fijos atractivos 2 Teoremas de puntos fijos 3 Véase también 4 Enlaces externos

Puntos fijos atractivos

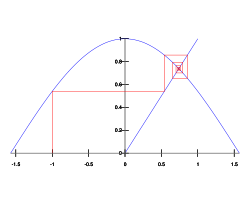
Un punto fijo atractivo de una función f es un punto fijo x ₀ de f tal que para cualquier valor de x en el dominio que es bastante cercano ax₀, la sucesión obtenida iterando la función

converge a x₀. Como de cerca es "bastante cerca" es a veces una cuestión sutil.

La función coseno natural ( "natural" significa en radianes, no grados u otras unidades) tiene exactamente un punto fijo, que es atractivo. En este caso "bastante cerca" no es nada restrictivo, para verlo se puede empezar con cualquier número real y pulsar repetidamente la tecla "cuerpo" de la calculadora. El resultado converge rápidamente a 0.73908513, que es un punto fijo. Aquí es donde la gráfica de la función coseno intersecar la recta y = x. No todos los puntos fijos son atractivos: por ejemplo, x = 0 es un punto fijo de la función f(x) = 2x, pero la iteración de esta función para cualquier punto distinto de cero diverge rápidamente. Ahora bien, si la función es continuamente derivable en un entorno abierto del punto fijox ₀ , y |f(x' ' ₀ ) | <1, entonces la atracción está garantizada. Los puntos fijos atractivos son un caso especial de un concepto matemático más amplio de atractores.

Se dice que un punto fijo atractivo es un punto fijo estable si es también Lyapunov estable ..

Se dice que un punto fijo estable es neutralmente estable si es Lyapunov estable pero no atrayente. El centro de una ecuación diferencial lineal homogénea de segundo orden es un ejemplo de un punto fijo neutralmente estable.

Teoremas de puntos fijos

Hay numerosos teoremas en diferentes partes de las matemáticas que garantizan a las funciones, si cumplen ciertas condiciones, tener al menos un punto fijo.

Véase también

• raíz
• Vector propio
• Equilibrio
• Atractor
• Teoría de la estabilidad
• Punto estacionario
• Invariante (matemáticas)
• Idempotente

Enlaces externos

• Animations for Fixed Point Iteration