Traslación (geometría)

Traslación (geometría)
Para otros usos de este término, véase Traslación (desambiguación).
Una traslación desplaza cada punto de una figura o espacio la misma cantidad en una determinada dirección.
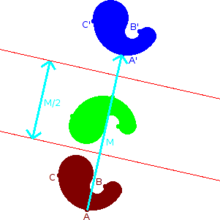Una reflexión respecto un eje seguida de otra reflexión respecto a otro eje paralelo al primero es equivalente a una traslación.

En geometría, una traslación es una isometría en el espacio euclídeo caracterizada por un vector \vec{u}, tal que, a cada punto P de un objeto o figura se le hace corresponder otro punto P' , tal que:

\begin{cases} T_\vec{u}:\R^n \to \R^n & \overrightarrow{PP'} = \vec{u}\\ P\mapsto P'=T(P)=P+\vec{u} \end{cases}

Definición de traslaciones

Las traslaciones pueden entenderse como movimientos directos sin cambios de orientación, es decir, mantienen la forma y el tamaño de las figuras u objetos trasladados, a las cuales deslizan según el vector. Dado el carácter de isometría para cualesquiera puntos P y Q se cumple la siguiente identidad entre distancias:

d(P,Q) = d(T(P),T(Q)) = d(P',Q')\;

Más aún se cumple que:

\overrightarrow{PQ} = \overrightarrow{P'Q'}

Notas:

  1. La figura trasladada es idéntica a la figura inicial.
  2. La figura trasladada conserva la misma orientación que la figura original.

Representación matricial

Puesto que una traslación es un caso particular de transformación afín pero no una transformación lineal, generalmente se usan coordenadas homogéneas para representar la traslación mediante una matriz y poder así expresarla como una transformación lineal sobre un espacio de dimensión superior.

Así un vector tridimensional w = (wx, wy, wz) puede ser reescrito usando cuatro coordenadas homogéneas comow = (wx, wy, wz, 1). En esas condiciones una traslación puede ser repretentada por una matriz como:

T_{\mathbf{v}} = \begin{bmatrix} 1 & 0 & 0 & v_x \\ 0 & 1 & 0 & v_y \\ 0 & 0 & 1 & v_z \\ 0 & 0 & 0 & 1 \end{bmatrix}

Ya que como puede verse, la multiplicación de esta matriz por la representación en coordenadas homogéneas de un vector da lugar al resultado esperado:

T_{\mathbf{v}} \mathbf{p} = \begin{bmatrix} 1 & 0 & 0 & v_x \\ 0 & 1 & 0 & v_y \\ 0 & 0 & 1 & v_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ p_z \\ 1 \end{bmatrix} = \begin{bmatrix} p_x + v_x \\ p_y + v_y \\ p_z + v_z \\ 1 \end{bmatrix} = \mathbf{p} + \mathbf{v} . \!

La inversa de una matriz de traslación puede obtenerse cambiando el signo de la dirección del vector desplazamiento

T^{-1}_{\mathbf{v}} = T_{-\mathbf{v}} . \!

Similarmente, el producto de dos matrices de traslación viene dado por:

T_{\mathbf{u}}T_{\mathbf{v}} = T_{\mathbf{u}+\mathbf{v}} . \!

Debido a que la suma de vectores es conmutativa, la multiplicaciónde matrices de traslación es también conmutativa, a diferencia de lo que sucede con matrices arbitrarias, que no necesariamente representan traslaciones.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Geometria taxicab — Saltar a navegación, búsqueda Distancia Manhattan contra distancia Euclideana: Las lineas rojo, azul y amarillas tienen la misma longitud (12) en las geometrias Euclideana y taxicab. En la geometria Euclideana, la linea verde tiene longitud… …   Wikipedia Español

  • Geometría molecular — Geometría de la molécula de agua. La geometría molecular o estructura molecular se refiere a la disposición tri dimensional de los átomos que constituyen una molécula. Determina muchas de las propiedades de las moléculas, como son la reactividad …   Wikipedia Español

  • Geometría afín — En la matemática, la geometría afín es el estudio de las propiedades geométricas que permancen inmutables bajo transformaciones afines, i.e. transformaciones lineales no singulares y traslaciones. El nombre de geometría afín así como el de… …   Wikipedia Español

  • Geometría taxicab — Distancia Manhattan contra distancia Euclideana: Las líneas rojo, azul y amarillas tienen la misma longitud (12) en las geometrías Euclideana y taxicab. En la geometría Euclideana, la línea verde tiene longitud 6×√2 ≈ 8.48, y es el… …   Wikipedia Español

  • Traslación — El término Traslación puede referirse a: Traslación, en geometría, movimiento de cada punto una distancia constante en una dirección dada. Traslación, en física, movimiento que cambia la posición de un objeto. Traslación de la Tierra, en… …   Wikipedia Español

  • Geometría constructiva de sólidos — Modelo de representación de objetos 3D en forma de árbol basado en dos elementos: Primitivas gráficas (esfera, cubo, cilindro, etc.) que se instancian en el espacio de coordenadas 3D suministrando valores de traslación (Tx,Ty,Tz), escalado (Sx,Sy …   Wikipedia Español

  • Homografía (geometría) — En geometría, se denomina homografía a toda transformación proyectiva que determina una correspondencia entre dos figuras geométricas planas, de forma que a cada uno de los puntos y las rectas de una de ellas le corresponden, respectivamente, un… …   Wikipedia Español

  • Rotación — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Transformación isométrica — Saltar a navegación, búsqueda La imajen de un objeto reflejada en un espejo plano, es un ejemplo de transformación isométrica: la simetría. Las transformaciones isométricas son transformaciones de figuras en el plano que se realizan sin variar… …   Wikipedia Español

  • Isometría afín — La imagen de un objeto reflejado en un espejo plano, es un ejemplo de transformación isométrica: la simetría. Las transformaciones isométricas son transformaciones de figuras en el plano que se realizan sin variar las dimensiones ni el área de… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”