En matemáticas, concretamente en la rama de la Topología, la compacidad es una de las muchas propiedades que puede adopar un espacio topológico. Se trata de una propiedad con gran importancia dado que dota a los espacios de una regularidad que permite definir teoremas u otras propiedades sobre estos espacios.

Formalmente un espacio topológico se dice que es compacto si es quasi-compacto y de Hausdorff. Vamos a definir cada concepto:

Espacios quasi-compactos: Sea (X,τ) un espacio topológico con su topología asociada. X es quasi-compacto si para todo recubrimiento por abiertos de X, es decir,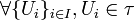 , existe un subrecubrimiento del mismo 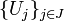, , 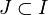, 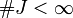finito.

Espacios de Hausdorff: Un espacio topológico (X,τ) es llamado espacio de Hausdorff o T₂ si para cada par de puntos, existen entornos en cada uno de ellos tal que su intersección es vacía, es decir, se pueden separar. Ésta es una propiedad de separación. Matemáticamente: (X,τ) es Hausdorff si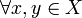 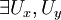entornos de x e y respectivamente tales que .

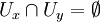Un resultado importante u otra definición equivalente de espacios Hausdorff sería definirlos del siguiente modo: Se dice que un espacio topológico (X,τ) es Hausdorff si, y sólo si la diagonal de X es un cerrado de .

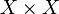Se define como diagonal de un conjunto a: 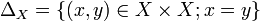. Si este conjunto es un cerrado de 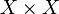entonces X es Hausdorff.

---

Definición:

Un espacio topológico (X,τ) es compacto si, y sólo si, es quasi-compacto y Hausdorff.

---

Una vez definido el concepto de compacidad podemos particularizarlo en conjuntos o espacios más conocidos como 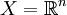, el espacio de dimensión n de números reales.

Existe un teorema que establece las condiciones necesarias y suficientes para que un subconjunto de 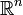sea compacto.

Teorema de Heine-Borel

Sea U un subconjunto de 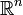, entonces U es compacto si, y sólo si es cerrado y acotado. Para ver la demostración puede verse el tema Teorema de Heine-Borel.

En particular todo subconjunto acotado de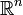 es quasi-compacto, puesto que 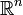o cualquier otro espacio no acotado, no permite subrecubrimientos finitos por abiertos, pero además como estamos considerando la topología euclídea, también es Hausdorff, lo que implica compacidad siempre que también sea cerrado.

En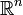 existe otro concepto totalmente equivalente de compacidad, esta vez utilizando sucesiones de números reales, recapitulando tenemos lo siguiente, restringidos a :

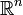Compacidad por recubrimientos:

U subconjunto de 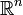es compacto por recubrimientos (dado que es Hausdorff) si para todo recubrimiento de U por abiertos admite un subrecubrimiento finito.

Compacidad por sucesiones:

U subconjunto de 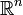es compacto por sucesiones si para toda sucesión de puntos, con límite o sin, admite una sucesión parcial convergente con límite en U.

Teorema: Un subconjunto de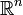 es compacto por recubrimientos si, y sólo si es compacto por sucesiones.

Este teorema nos muestra que ambas definiciones son equivalentes.